2020-2021学年一 圆柱和圆锥综合与测试课时训练

这是一份2020-2021学年一 圆柱和圆锥综合与测试课时训练，共7页。试卷主要包含了圆锥有条高，圆柱体的侧面展开，不可能得到等内容，欢迎下载使用。
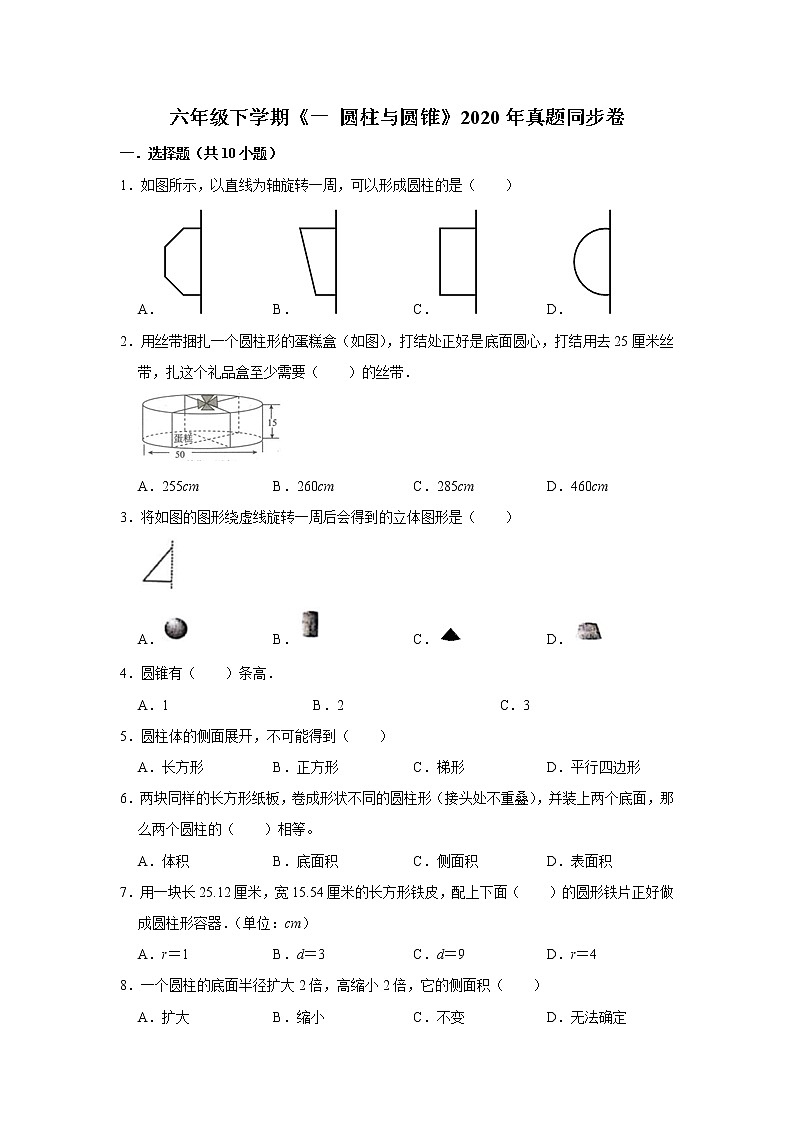
1．如图所示，以直线为轴旋转一周，可以形成圆柱的是（ ）
A．B．C．D．
2．用丝带捆扎一个圆柱形的蛋糕盒（如图），打结处正好是底面圆心，打结用去25厘米丝带，扎这个礼品盒至少需要（ ）的丝带．
A．255cmB．260cmC．285cmD．460cm
3．将如图的图形绕虚线旋转一周后会得到的立体图形是（ ）
A．B．C．D．
4．圆锥有（ ）条高．
A．1B．2C．3
5．圆柱体的侧面展开，不可能得到（ ）
A．长方形B．正方形C．梯形D．平行四边形
6．两块同样的长方形纸板，卷成形状不同的圆柱形（接头处不重叠），并装上两个底面，那么两个圆柱的（ ）相等。
A．体积B．底面积C．侧面积D．表面积
7．用一块长25.12厘米，宽15.54厘米的长方形铁皮，配上下面（ ）的圆形铁片正好做成圆柱形容器．（单位：cm）
A．r＝1B．d＝3C．d＝9D．r＝4
8．一个圆柱的底面半径扩大2倍，高缩小2倍，它的侧面积（ ）
A．扩大B．缩小C．不变D．无法确定
9．一个圆柱与一个圆锥的底面积和体积都相等．已知圆柱的高是4dm，圆锥的高是（ ）dm．
A．12B．4C．8
10．如图所示，把一张三条边长分别是5cm、12cm和13cm的直角三角形硬纸贴在木棒上，快速转动木棒，转出的圆锥高是___cm，底面半径是___cm．（ ）
A．5，12B．12，5C．13，5D．12，13
二．填空题（共5小题）
11．一个长方形绕一条长边旋转一周所形成的立体图形是 ．
12．（单位：cm）以直角三角形的长直角边为轴旋转一周（如图）得到几何体是 ，体积是
cm3．
13．圆柱的侧面展开后的图形是 ，圆锥的侧面展开后的图形是 ．
14．如图，瓶底的面积和锥形高脚杯口的面积相等，将瓶子中的液体倒入锥形杯子中，能倒满 杯．（瓶壁与杯壁的厚度忽略不计）
15．一个圆柱和一个圆锥的底面周长相等，圆锥的高是圆柱的3倍，圆锥的体积是12立方分米，圆柱的体积是 立方分米．
三．解答题（共5小题）
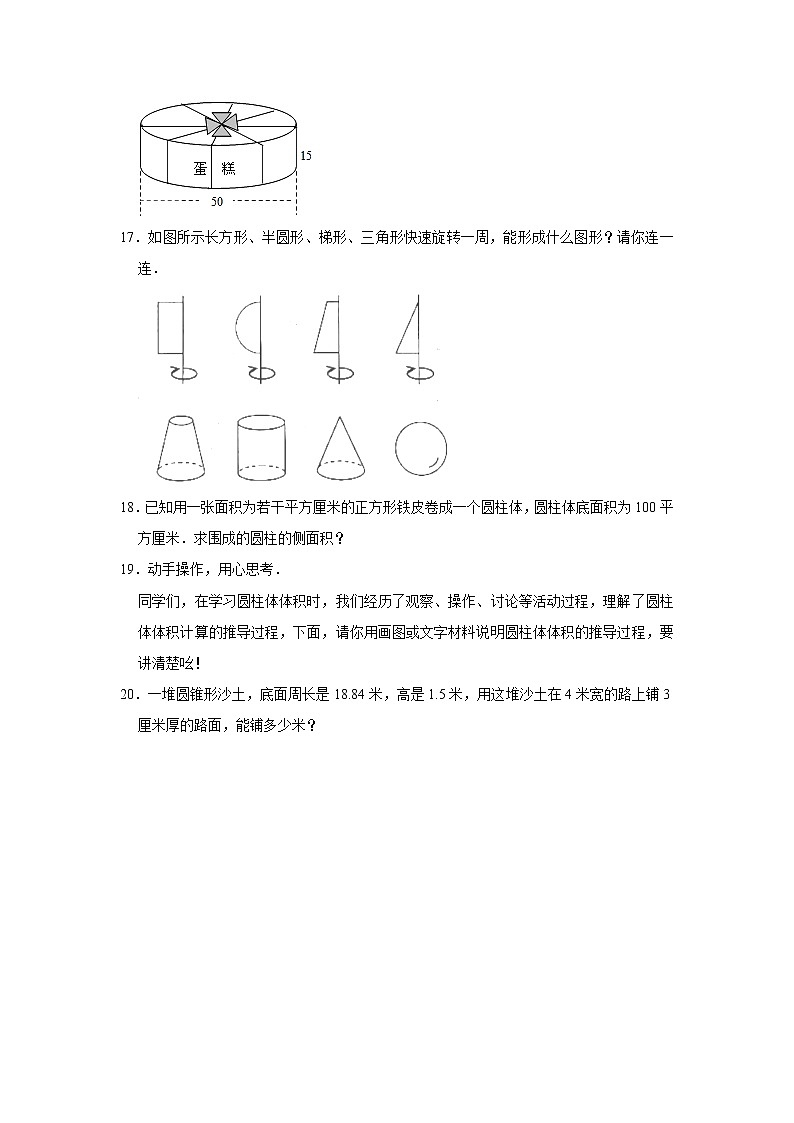
16．用塑料绳捆扎一个圆柱形的蛋糕盒（如图，单位：厘米），打结处正好是底面圆心，打结用去绳长25厘米．扎这个盒子至少用去塑料绳多少厘米？在它的整个侧面贴上商标和说明，这部分的面积是多少平方厘米？
17．如图所示长方形、半圆形、梯形、三角形快速旋转一周，能形成什么图形？请你连一连．
18．已知用一张面积为若干平方厘米的正方形铁皮卷成一个圆柱体，圆柱体底面积为100平方厘米．求围成的圆柱的侧面积？
19．动手操作，用心思考．
同学们，在学习圆柱体体积时，我们经历了观察、操作、讨论等活动过程，理解了圆柱体体积计算的推导过程，下面，请你用画图或文字材料说明圆柱体体积的推导过程，要讲清楚吆！
20．一堆圆锥形沙土，底面周长是18.84米，高是1.5米，用这堆沙土在4米宽的路上铺3厘米厚的路面，能铺多少米？
六年级下学期《一 圆柱与圆锥》2020年真题同步卷
参考答案与试题解析
一．选择题（共10小题）
1．【解答】解：因为圆柱从正面看到的是一个长方形，所以以直线为轴旋转一周，可以形成圆柱的是长方形，
故选：C．
2．【解答】解：50×4+15×4+25
＝200+60+25
＝285（厘米）
答：扎这个礼品盒至少需要285厘米的丝带．
故选：C。
3．【解答】解：一个直角三角形围绕一条直角边为中心对称轴旋转一周形成一个圆锥体，
故选：C．
4．【解答】解：根据圆锥的高的定义可知：圆锥只有一条高．
故选：A．
5．【解答】解：圆柱的侧面沿高展开是长方形或正方形，如果沿斜线展开得到的图形是一个平行四边形，侧面无论怎样展开绝对不是梯形；
故选：C．
6．【解答】解：两块同样的长方形纸板，卷成形状不同的圆柱形（接头处不重叠），并装上两个底面，那么两个圆柱的侧面积相等。
故选：C。
7．【解答】解：25.12÷3.14÷2＝4（厘米）
15.54÷3.14÷2
≈4.95÷2
＝2.475（厘米）
答：配上下面半径是4厘米的圆形铁片正好做成圆柱形容器．
故选：D。
8．【解答】解：一个圆柱的底面半径扩大2倍，高缩小2倍，它的侧面积不变。
故选：C。
9．【解答】解：4×3＝12（dm）
答：圆锥的高是12dm．
故选：A．
10．【解答】解：将三角形围着一条直角边旋转得到一个圆锥，这条直角边就是圆锥的高，即12cm，另一条直角边就是圆锥的底面半径，即5cm．
答：转出的圆锥高是12cm，底面半径是5cm．
故选：B．
二．填空题（共5小题）
11．【解答】解：根据圆柱体的特征，一个长方形绕它的一条边旋转，可以形成一个圆柱体；
故答案为：圆柱．
12．【解答】解：（1）以4cm的直角边为轴旋转一周，可以得到一个立体图形，这个立体图形是圆锥体；
（2）×3.14×32×4
＝3.14×3×4
＝37.68（立方厘米）
故答案为：圆锥体，37.68．
13．【解答】解：圆柱的侧面展开图是长方形，圆锥的侧面展开图扇形．
故答案为：长方形，扇形．
14．【解答】解：3×2＝6（杯）
答：能倒满6杯。
故答案为：6。
15．【解答】解：一个圆柱和一个圆锥的底面周长相等，则底面半径就相等，则它们的底面积就相等，
圆柱的体积＝底面积×高，
圆锥的体积＝×底面积×高，
圆锥的高是圆柱的3倍，所以圆柱和圆锥的体积相等，也是12立方分米．
故答案为：12．
三．解答题（共5小题）
16．【解答】解：（1）15×8+50×8+25，
＝120+400+25，
＝545（厘米），
面积：3.14×50×15，
＝157×15，
＝2355（平方厘米）；
答：扎这个盒子至少用去塑料绳545厘米，在它的整个侧面贴上商标和说明，这部分的面积是2355平方厘米．
17．【解答】解：第一个长方形旋转一周，得到的是圆柱；
第二个半圆形旋转一周，得到的是球体
第三个梯形旋转一周，得到的是圆台；
第四个三角形旋转一周，得到的是圆锥；
18．【解答】解：设这个圆柱的底面半径为r，则πr2＝100
所以r2＝
围成的圆柱的侧面积即这个正方形的面积：
2πr×2πr＝4π2r2＝4π2×＝400π＝400×3.14＝1256（平方厘米）
答：围成的圆柱的侧面积是1256平方厘米．
19．【解答】解：如图：把一个圆柱平均分成若干份，然后沿底面半径和高切开，拼成一个近似长方体，拼成的长方体的底面积等于圆柱的底面积，拼成的长方体的高等于圆柱的高，因为长方体的体积＝底面积×高，所以圆柱的体积＝底面积×高．
20．【解答】解：圆锥形沙土的体积：
×3.14×（18.84÷3.14÷2）2×1.5
＝×3.14×32×1.5
＝3.14×9×0.5
＝14.13（立方米）；
能铺路面的长度：
3厘米＝0.03米
14.13÷（4×0.03）
＝14.13÷0.12
＝117.75（米）
答：能铺117.75米长．

26:58；