2021年广东省深圳市罗湖区中考数学三模试卷

这是一份2021年广东省深圳市罗湖区中考数学三模试卷，共25页。

2021年广东省深圳市罗湖区中考数学三模试卷
一.选择题（每小题3分共30分）
1．（3分）如图，数轴上点A所表示的数的绝对值是（　　）

A．2 B． C． D．﹣2
2．（3分）下列图形中，既不是中心对称图形，也不是轴对称图形的是（　　）
A． B．
C． D．
3．（3分）据统计，某城市去年接待旅游人数约为89 000 000人，89 000 000这个数据用科学记数法表示为（　　）
A．8.9×106 B．8.9×105 C．8.9×107 D．8.9×108
4．（3分）如图是由四个相同的小正方体组成的几何体，若从正面观察该几何体，得到的形状图是（　　）

A． B．
C． D．
5．（3分）甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好是9.4环，方差分别是S甲2＝0.90，S乙2＝1.22，S丙2＝0.45，S丁2＝1.9，在本次射击测试中，成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
6．（3分）下列运算正确的是（　　）
A．x3+x3＝x6 B．a12÷a4＝a3 C．（a3）2＝a5 D．a7•a5＝a12
7．（3分）如图，已知l1∥l2，将一个含45°角的三角尺按图中方式放置，∠1＝24°，则∠2的大小是（　　）

A．21° B．24° C．30° D．66°
8．（3分）如图，用尺规作角平分线，根据作图步骤，在说明射线AN是∠BAC的平分线过程中，以下说法错误的是（　　）

A．由作弧可知AE＝AF B．由作弧可知FP＝EP
C．由SAS 证明△AFP≌△AEP D．由SSS证明△AFP≌△AEP
9．（3分）函数y＝x2+bx+c与y＝x的图象如图所示，有以下结论：
①b2﹣4c＞0；②b+c+1＝0；③3b+c+6＝0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．
其中正确的个数为（　　）

A．1 B．2 C．3 D．4
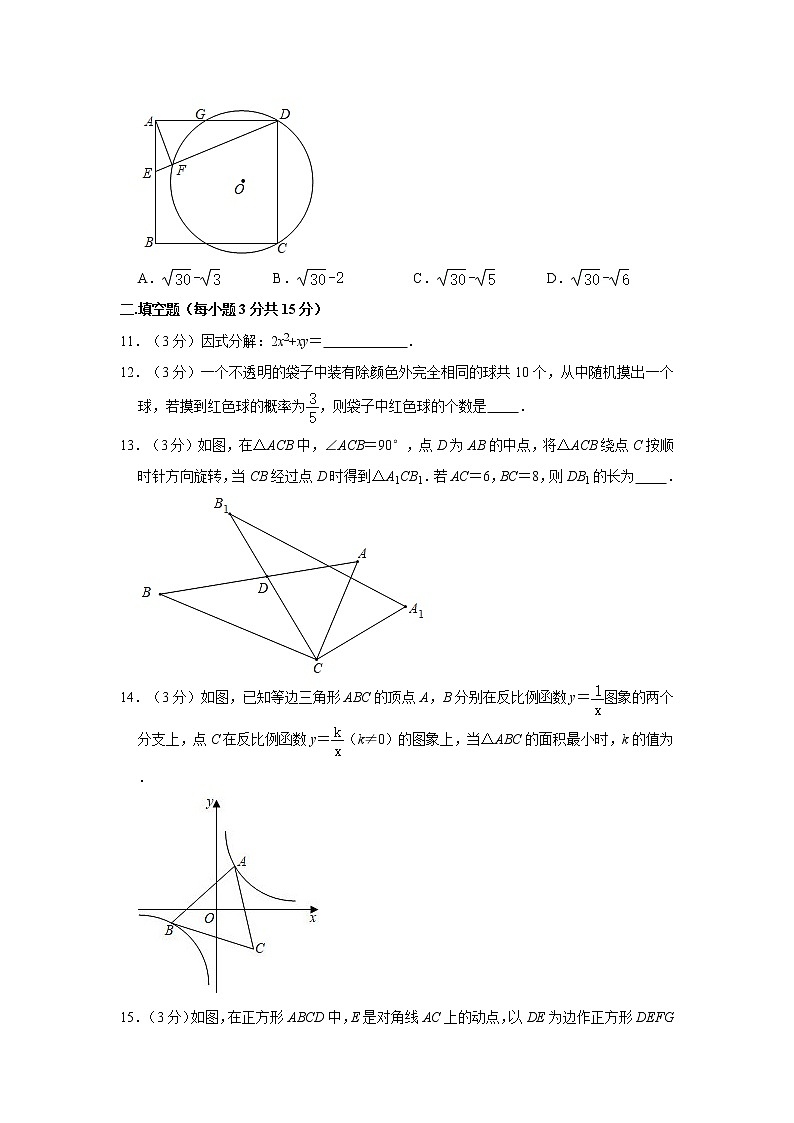
10．（3分）如图，正方形ABCD中，E为AB上一点，AF⊥DE于点F，已知DF＝5EF＝5，过C、D、F的⊙O与边AD交于点G，则DG＝（　　）

A． B． C． D．
二.填空题（每小题3分共15分）
11．（3分）因式分解：2x2+xy＝　 　．
12．（3分）一个不透明的袋子中装有除颜色外完全相同的球共10个，从中随机摸出一个球，若摸到红色球的概率为，则袋子中红色球的个数是　 　．
13．（3分）如图，在△ACB中，∠ACB＝90°，点D为AB的中点，将△ACB绕点C按顺时针方向旋转，当CB经过点D时得到△A1CB1．若AC＝6，BC＝8，则DB1的长为　 　．

14．（3分）如图，已知等边三角形ABC的顶点A，B分别在反比例函数y＝图象的两个分支上，点C在反比例函数y＝（k≠0）的图象上，当△ABC的面积最小时，k的值为　 　．

15．（3分）如图，在正方形ABCD中，E是对角线AC上的动点，以DE为边作正方形DEFG，H是CD的中点．连接GH，若GH的最小值是1，则正方形ABCD的边长为　 　．

三、解答题（本大题共7小题，其中第16题5分，第17题6分，第18题8分，第19题8分,第20题8分，第21题10分，第22题10分，共55分)
16．（5分）计算：2﹣1+sin30°+﹣（﹣tan60°）0．
17．（6分）解方程：
（1）＝；
（2）x2+6x﹣2＝0．
18．（8分）为弘扬中华优秀传统文化，某校开展了“经典雅韵”诵读比赛活动，现随机抽取部分同学的成绩进行统计，并绘制如下两个不完整的统计图，请结合图中提供的信息，解答下列各题：

（1）直接写出a的值，a＝　 　，并把频数分布直方图补充完整．
（2）求扇形B的圆心角度数．
（3）如果全校有2000名学生参加这次活动，90分以上（含90分）为优秀，那么估计获得优秀奖的学生有多少人？．
19．（8分）如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，点D为⊙O上一点，且CD＝CB，连接DO并延长交CB的延长线于点E．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若BE＝4，DE＝8，求AC的长．

20．（8分）某学校为丰富同学们的课余生活，购买了一批数量相等的象棋和围棋兴趣小组使用，其中购买象棋用了210元，购买围棋用了378元，已知每副围棋比每副象棋贵8元．
（1）求每副围棋和象棋各是多少元？
（2）若该校决定再次购买同种围棋和象棋共50副，且再次购买的费用不超过600元，则该校最多可再购买多少副围棋？
21．（10分）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．
（1）直接写出抛物线的解析式：　 　；
（2）点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H，设点D的横坐标为m．
①求DF+HF的最大值；
②连接EG，若∠GEH＝45°时，求m的值．

22．（10分）在平面直角坐标系中，O为原点，四边形ABCD是矩形，点A（0，2），C（2，0），点D是对角线AC上一点（不与A、C重合），连接BD，作DE⊥BD，交x轴于点E，以线段DE、DB为邻边作矩形BDEF．
（1）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长；若不存在，请说明理由；
（2）求证：；
（3）设AD＝x，矩形BDEF的面积为y，求y关于x的函数关系式，并求出当x取何值时，y有最小值？


2021年广东省深圳市罗湖区中考数学三模试卷
参考答案与试题解析
一.选择题（每小题3分共30分）
1．（3分）如图，数轴上点A所表示的数的绝对值是（　　）

A．2 B． C． D．﹣2
【分析】观察数轴易知点A表示的数为﹣2，找到﹣2的绝对值即可．
【解答】解：由题易知点A表示的数为﹣2，
∵|﹣2|＝2，
故选：A．
2．（3分）下列图形中，既不是中心对称图形，也不是轴对称图形的是（　　）
A． B．
C． D．
【分析】结合选项根据轴对称图形与中心对称图形的概念求解即可．
【解答】解：A、既是轴对称图形，也是中心对称图形，不合题意；
B、是轴对称图形，不是中心对称图形，不合题意；
C、不是轴对称图形，是中心对称图形，不合题意；
D、既不是轴对称图形，也不是中心对称图形，符合题意．
故选：D．
3．（3分）据统计，某城市去年接待旅游人数约为89 000 000人，89 000 000这个数据用科学记数法表示为（　　）
A．8.9×106 B．8.9×105 C．8.9×107 D．8.9×108
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【解答】解：89 000 000这个数据用科学记数法表示为8.9×107．
故选：C．
4．（3分）如图是由四个相同的小正方体组成的几何体，若从正面观察该几何体，得到的形状图是（　　）

A． B．
C． D．
【分析】根据主视图是从物体正面看所得到的图形解答即可．
【解答】解：从正面看有两层，底层是三个正方形，上层右边是一个正方形，右齐．
故选：D．
5．（3分）甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好是9.4环，方差分别是S甲2＝0.90，S乙2＝1.22，S丙2＝0.45，S丁2＝1.9，在本次射击测试中，成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
【分析】根据方差的意义求解即可．
【解答】解：∵S甲2＝0.90，S乙2＝1.22，S丙2＝0.45，S丁2＝1.9，
∴S丙2＜S甲2＜S乙2＜S丁2，
∴在本次射击测试中，成绩最稳定的是丙，
故选：C．
6．（3分）下列运算正确的是（　　）
A．x3+x3＝x6 B．a12÷a4＝a3 C．（a3）2＝a5 D．a7•a5＝a12
【分析】分别计算各选项即可．
【解答】解：A．x3+x3＝2x3，该选项不正确，不符合题意；
B．a12÷a4＝a8，该选项错误，不符合题意；
C．（a3）2＝a6，该选项错误，不符合题意；
D．a7•a5＝a12，该选项正确，符合题意．
故选：D．
7．（3分）如图，已知l1∥l2，将一个含45°角的三角尺按图中方式放置，∠1＝24°，则∠2的大小是（　　）

A．21° B．24° C．30° D．66°
【分析】过B作BD∥l1得到BD∥l1∥l2，根据平行线的性质证得∠ABD＝∠1，∠2＝∠CBD，由含45°角的三角尺锐角的度数求出∠CBD的度数，即可得到∠2的大小．
【解答】解：过B作BD∥l1，
∵l1∥l2，
∴BD∥l1∥l2，
∴∠ABD＝∠1，∠2＝∠CBD，
∵∠1＝24°，
∴∠ABD＝24°，
∵∠ABC＝45°，
∴∠ABD+∠CBD＝45°，
∴∠CBD＝∠ABC﹣∠ABD＝21°，
∴∠2＝21°，
故选：A．

8．（3分）如图，用尺规作角平分线，根据作图步骤，在说明射线AN是∠BAC的平分线过程中，以下说法错误的是（　　）

A．由作弧可知AE＝AF B．由作弧可知FP＝EP
C．由SAS 证明△AFP≌△AEP D．由SSS证明△AFP≌△AEP
【分析】由作图可知，AF＝AE，PF＝PE结合全等三角形的判定可得结论．
【解答】解：连接PF，PE．

由作图可知，AF＝AE，PF＝PE，
∵AP＝AP，
∴△APF≌△APE（SSS），
故选项A，B，D正确，
故选：C．
9．（3分）函数y＝x2+bx+c与y＝x的图象如图所示，有以下结论：
①b2﹣4c＞0；②b+c+1＝0；③3b+c+6＝0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．
其中正确的个数为（　　）

A．1 B．2 C．3 D．4
【分析】由函数y＝x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x＝1时，y＝1+b+c＝1；当x＝3时，y＝9+3b+c＝3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．
【解答】解：∵函数y＝x2+bx+c与x轴无交点，
∴b2﹣4c＜0；
故①错误；
当x＝1时，y＝1+b+c＝1，
故②错误；
∵当x＝3时，y＝9+3b+c＝3，
∴3b+c+6＝0；
③正确；
∵当1＜x＜3时，二次函数值小于一次函数值，
∴x2+bx+c＜x，
∴x2+（b﹣1）x+c＜0．
故④正确．
故选：B．
10．（3分）如图，正方形ABCD中，E为AB上一点，AF⊥DE于点F，已知DF＝5EF＝5，过C、D、F的⊙O与边AD交于点G，则DG＝（　　）

A． B． C． D．
【分析】连接CF、GF，由△AFD∽△EAD可得正方形边长，再由△AFG∽△DFC即可得到答案．
【解答】解：连接CF、GF，如图：


∵正方形ABCDA中，∠EAD＝∠ADC＝90°，AF⊥DE，
∴△AFD∽△EAD，
∴＝，
又∵DF＝5EF＝5，
∴AD＝＝＝＝CD，
在Rt△AFD中，AF＝＝＝，
∵∠CDF+∠ADF＝90°，∠DAF+∠ADF＝90°，
∴∠DAF＝∠CDF，
∵四边形GFCD是⊙OO的内接四边形，
∴∠FCD+∠DGF＝180°，
∵∠FGA+∠DGF＝180°
∴∠FGA＝∠FCD，
∴△AFG∽△DFC
∴＝，
∴＝，
∴AG＝，
∴DG＝AD﹣AG＝﹣，
故选：D．
二.填空题（每小题3分共15分）
11．（3分）因式分解：2x2+xy＝　x（2x+y）　．
【分析】直接提取公因式y，进而分解因式即可．
【解答】解：2x2+xy＝x（2x+y）．
故答案为：x（2x+y）．
12．（3分）一个不透明的袋子中装有除颜色外完全相同的球共10个，从中随机摸出一个球，若摸到红色球的概率为，则袋子中红色球的个数是　6　．
【分析】首先设袋子中红球有x个，利用概率公式求即可得方程，进而解答即可．
【解答】解：设袋子中红球有x个，根据题意可得：，
解得：x＝6，
故答案为：6．
13．（3分）如图，在△ACB中，∠ACB＝90°，点D为AB的中点，将△ACB绕点C按顺时针方向旋转，当CB经过点D时得到△A1CB1．若AC＝6，BC＝8，则DB1的长为　3　．

【分析】根据勾股定理得到AB＝＝＝10，由直角三角形的性质的CD＝AB＝5，由旋转的性质得到CB1＝BC＝8，于是得到结论．
【解答】解：∵在△ACB中，∠ACB＝90°，AC＝6，BC＝8，
∴AB＝＝＝10，
∵点D为AB的中点，
∴CD＝AB＝5，
∵将△ACB绕点C按顺时针方向旋转，当CB经过点D时得到△A1CB1．
∴CB1＝BC＝8，
∴DB1＝8﹣5＝3，
故答案为：3．
14．（3分）如图，已知等边三角形ABC的顶点A，B分别在反比例函数y＝图象的两个分支上，点C在反比例函数y＝（k≠0）的图象上，当△ABC的面积最小时，k的值为　﹣3　．

【分析】当等边三角形ABC的边长最小时，△ABC的面积最小，点A，B分别在反比例函数y＝图象的两个分支上，则当A、B在直线y＝x上时最短，即此时△ABC的面积最小，根据反比例函数图象的对称性可得OA＝OB，设OA＝x，则AC＝2x，OC＝x，根据等边三角形三线合一可证明△AOE∽△OCF，根据相似三角形面积比等于相似比的平方可得结论．
【解答】解：根据题意当A、B在直线y＝x上时，△ABC的面积最小，
函数y＝图象关于原点对称，
∴OA＝OB，
连接OC，过A作AE⊥y轴于E，过C作CF⊥y轴于F，
∵△ABC是等边三角形，
∴AO⊥OC，
∴∠AOC＝90°，∠ACO＝30°，
∴∠AOE+∠COF＝90°，
设OA＝x，则AC＝2x，OC＝x，
∵AE⊥y轴，CF⊥y轴，
∴∠AEO＝∠OFC＝∠AOE+∠OAE＝90°，
∴∠COF＝∠OAE，
∴△AOE∽△OCF，
∴＝（）2＝（）2＝，
∵顶点A在函数y＝图象的分支上，
∴S△AOE＝，
∴S△OCF＝，
∵点C在反比例函数y＝（k≠0）的图象上，
∴k＝﹣3，
故答案为﹣3．

15．（3分）如图，在正方形ABCD中，E是对角线AC上的动点，以DE为边作正方形DEFG，H是CD的中点．连接GH，若GH的最小值是1，则正方形ABCD的边长为　2　．

【分析】连接CG．证明△ADE≌△CDG（SAS），推出∠DCG＝∠DAE＝45°，推出点G的运动轨迹是射线CG，根据垂线段最短可知，当GH⊥CG时，GH的值最小，再解直角三角形求得CH，便可得正方形ABCD的边长．
【解答】解：连接CG．

∵四边形ABCD是正方形，四边形DECG是正方形，
∴DA＝DC，DE＝DG，∠ADC＝∠EDG＝90°，∠DAC＝45°，
∴∠ADE＝∠CDG，
∴△ADE≌△CDG（SAS），
∴∠DCG＝∠DAE＝45°，
∴点G的运动轨迹是射线CG，
根据垂线段最短可知，当GH⊥CG时，GH的值最小为1，
∴CH＝．
∴CD＝2CH＝2，
故答案为：2．
三、解答题（本大题共7小题，其中第16题5分，第17题6分，第18题8分，第19题8分,第20题8分，第21题10分，第22题10分，共55分)
16．（5分）计算：2﹣1+sin30°+﹣（﹣tan60°）0．
【分析】利用零指数幂、负整数指数幂法则以及二次根式的性质计算即可得到结果．
【解答】解：原式＝
＝．
17．（6分）解方程：
（1）＝；
（2）x2+6x﹣2＝0．
【分析】（1）先把分式方程整理成整式方程，再按照解整式方程的步骤进行计算，最后再进行检验，即可得出答案．
（2）根据配方法的步骤先把﹣2移到等号的右边配方，再进行配方，求出x的值．
【解答】解：（1）＝，
5（x﹣1）＝6x，
5x﹣6x＝5，
﹣x＝5，
x＝﹣5，
经检验x＝﹣5是原方程的根，
则原方程的解是x＝﹣5；

（2）x2+6x﹣2＝0
x2+6x＝2，
x2+6x+9＝2+9，
（x+3）2＝11，
x+3＝，
x1＝﹣3﹣，x2＝﹣3+；
18．（8分）为弘扬中华优秀传统文化，某校开展了“经典雅韵”诵读比赛活动，现随机抽取部分同学的成绩进行统计，并绘制如下两个不完整的统计图，请结合图中提供的信息，解答下列各题：

（1）直接写出a的值，a＝　30　，并把频数分布直方图补充完整．
（2）求扇形B的圆心角度数．
（3）如果全校有2000名学生参加这次活动，90分以上（含90分）为优秀，那么估计获得优秀奖的学生有多少人？．
【分析】（1）先根据E等级人数及其占总人数的比例可得总人数，再用D等级人数除以总人数可得a的值，用总人数减去其他各等级人数求得C等级人数可补全图形；
（2）用360°乘以A等级人数所占比例可得；
（3）用总人数乘以样本中E等级人数所占比例．
【解答】解：（1）∵被调查的总人数为10÷＝50（人），
∴D等级人数所占百分比a%＝×100%＝30%，即a＝30，
C等级人数为50﹣（5+7+15+10）＝13人，
补全图形如下：

故答案为：30；

（2）扇形B的圆心角度数为360°×＝50.4°；

（3）估计获得优秀奖的学生有2000×＝400人．
19．（8分）如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，点D为⊙O上一点，且CD＝CB，连接DO并延长交CB的延长线于点E．
（1）判断直线CD与⊙O的位置关系，并说明理由；
（2）若BE＝4，DE＝8，求AC的长．

【分析】（1）欲证明CD是切线，只要证明OD⊥CD，利用全等三角形的性质即可证明；
（2）设⊙O的半径为r．在Rt△OBE中，根据OE2＝EB2+OB2，可得（8﹣r）2＝r2+42，推出r＝3，由tan∠E＝＝，推出＝，可得CD＝BC＝6，再利用勾股定理即可解决问题；
【解答】（1）证明：连接OC．

∵CB＝CD，CO＝CO，OB＝OD，
∴△OCB≌△OCD，
∴∠ODC＝∠OBC＝90°，
∴OD⊥DC，
∴DC是⊙O的切线．

（2）解：设⊙O的半径为r．
在Rt△OBE中，∵OE2＝EB2+OB2，
∴（8﹣r）2＝r2+42，
∴r＝3，
∵tan∠E＝＝，
∴＝，
∴CD＝BC＝6，
在Rt△ABC中，AC＝＝＝6．
20．（8分）某学校为丰富同学们的课余生活，购买了一批数量相等的象棋和围棋兴趣小组使用，其中购买象棋用了210元，购买围棋用了378元，已知每副围棋比每副象棋贵8元．
（1）求每副围棋和象棋各是多少元？
（2）若该校决定再次购买同种围棋和象棋共50副，且再次购买的费用不超过600元，则该校最多可再购买多少副围棋？
【分析】（1）设每副围棋x元，则每副象棋（x﹣8）元，根据210元购买象棋数量＝378元购买围棋数量列出方程并解答；
（2）设购买围棋m副，则购买象棋（50﹣m）副，根据题意列出不等式并解答．
【解答】解：（1）设每副围棋x元，则每副象棋（x﹣8）元，
根据题意，得．
解得x＝18．
经检验x＝18是所列方程的根．
所以x﹣8＝10．
答：每副围棋18元，每副象棋10元；
（2）设再次购买围棋m副，则购买象棋（50﹣m）副，
根据题意，得18m+10（50﹣m）≤600．
解得m≤12.5．
因m只能取整数，
故m最大值是12．
答：该校最多可再购买12副围棋．
21．（10分）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．
（1）直接写出抛物线的解析式：　y＝﹣x2+2x+3　；
（2）点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴交于点G、H，设点D的横坐标为m．
①求DF+HF的最大值；
②连接EG，若∠GEH＝45°时，求m的值．

【分析】（1）用待定系数法即可求解；
（2）①设D（m，﹣m2+2m+3），F（m，﹣m+3），则＝（﹣m2+2m+3）﹣（﹣m+3）+2m，进而求解；
②由∠GEH＝∠EFH，∠EHF是公共角得到△EHG∽△FHE，则，得到，进而求解．
【解答】解：（1）设抛物线的表达式为y＝a（x﹣x1）（x﹣x2），
将点A、B的坐标代入上式得：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3，
故答案为：y＝﹣x2+2x+3；

（2）①当x＝0时，y＝﹣x2+2x+3＝3，
∴点C（0，3）．
设直线BC的解析式为y＝mx+n，
把B（3，0），C（0，3）代入，得，解得，
∴BC的解析式为：y＝﹣x+3．
∵OB＝OC＝3，
∴∠OBC＝∠OCB＝45°．
作FK⊥y轴于点K，

又∵FH⊥BC，
∴∠KFH＝∠KHF＝45°，
∴．
设D（m，﹣m2+2m+3），F（m，﹣m+3），
∴＝（﹣m2+2m+3）﹣（﹣m+3）+2m，
整理得：．
由题意有0＜m＜3，且，﹣1＜0，
当时，取最大值，的最大值为；

②作GM⊥y轴于点M，记直线FH与x轴交于点N．
∵FK⊥y轴，DE⊥x轴，∠KFH＝45°，
∴∠EFH＝∠ENF＝45°，
∴EF＝EN．
∵∠KHF＝∠ONH＝45°，
∴OH＝ON．
∵y＝﹣x2+2x+3的对称轴为x＝1，
∴MG＝1，
∵∠KHF＝45°，
∴．
∵∠GEH＝45°，
∴∠GEH＝∠EFH．
又∵∠EHF是公共角，
∴△EHG∽△FHE，
∴，
∴，
在Rt△ONH中，OH＝ON＝|OE﹣EN|＝|OE﹣EF|＝|m﹣（﹣m+3）|＝|2m﹣3|，OE＝m，
在Rt△OEH中，
∵HE2＝OE2+OH2＝m2+（2m﹣3）2＝5m2﹣12m+9，
∴5m2﹣12m+9＝2m，
解得m1＝1，．
22．（10分）在平面直角坐标系中，O为原点，四边形ABCD是矩形，点A（0，2），C（2，0），点D是对角线AC上一点（不与A、C重合），连接BD，作DE⊥BD，交x轴于点E，以线段DE、DB为邻边作矩形BDEF．
（1）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长；若不存在，请说明理由；
（2）求证：；
（3）设AD＝x，矩形BDEF的面积为y，求y关于x的函数关系式，并求出当x取何值时，y有最小值？

【分析】（1）由锐角三角函数可求∠ACO＝30°，∠ACB＝60°，分两种情况讨论，由等腰三角形的性质可求解；
（2）通过证明△BMD∽△DNE，可得结论；
（3）由勾股定理可求BD2的值，由面积公式可求解析式，即可求解．
【解答】解：（1）存在；理由如下：
∵点A（0，2），C（2，0），
∴OA＝2，OC＝2，
∵tan∠ACO＝，
∴∠ACO＝30°，∠ACB＝60°，
分两种情况：
①当E在线段CO上时，△DEC是等腰三角形，观察图像可知，只有ED＝EC，如图1所示：

∴∠DCE＝∠EDC＝30°，
∴∠DBC＝∠BCD＝60°，
∴△DBC是等边三角形，
∴DC＝BC＝2，
在Rt△AOC中，∠ACO＝30°，OA＝2，
∴AC＝2AO＝4，
∴AD＝AC﹣CD＝4﹣2＝2，
∴当AD＝2时，△DEC是等腰三角形；
②当E在OC的延长线上时，△DCE是等腰三角形，只有CD＝CE，∠DBC＝∠DEC＝∠CDE＝15°，如图2所示：

∴∠ABD＝∠ADB＝75°，
∴AB＝AD＝2，
综上所述，满足条件的AD的值为2或2；
（2）证明：过点D作MN⊥AB交AB于M，交OC于N，如图3所示：

设DN＝a，
∵∠ACO＝30°，
∴，
∵∠BDE＝90°，
∴∠BDM+∠NDE＝90°，∠BDM+∠DBM＝90°，
∴∠DBM＝∠EDN，
∵∠BMD＝∠DNE＝90°，
∴△BMD∽△DNE，
∴；
（3）作DH⊥AB于H，如图4所示：

在Rt△ADH中，AD＝x，∠DAH＝∠ACO＝30°，
∴DH＝AD＝x，，
∴BH＝2﹣x，
在Rt△BDH中，BD2＝，
由（2）得，
∴，
∴矩形BDEF的面积为，
∴，
∵＞0，
∴x＝3时，y有最小值为，
即当点D运动到距A点的距离为3时，y有最小值．