



专题24 手拉手模型问题-2021年中考数学二轮复习经典问题专题训练
展开专题24 手拉手模型问题
【规律总结】
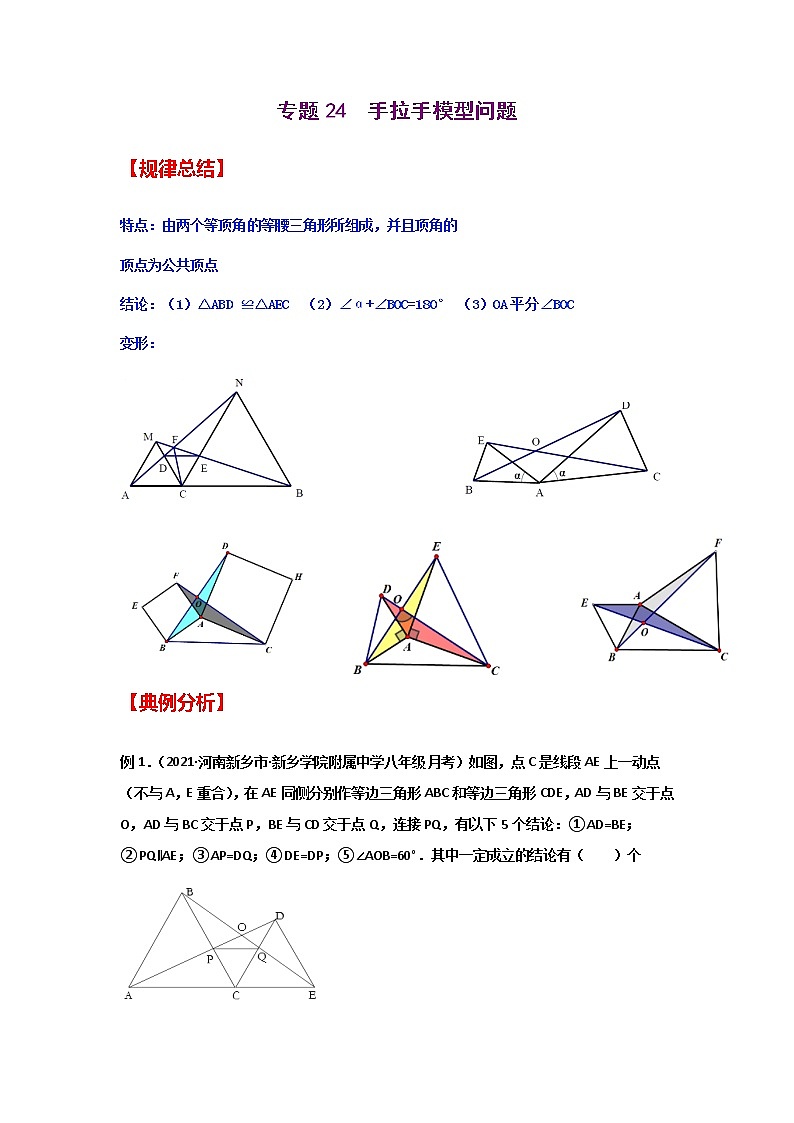
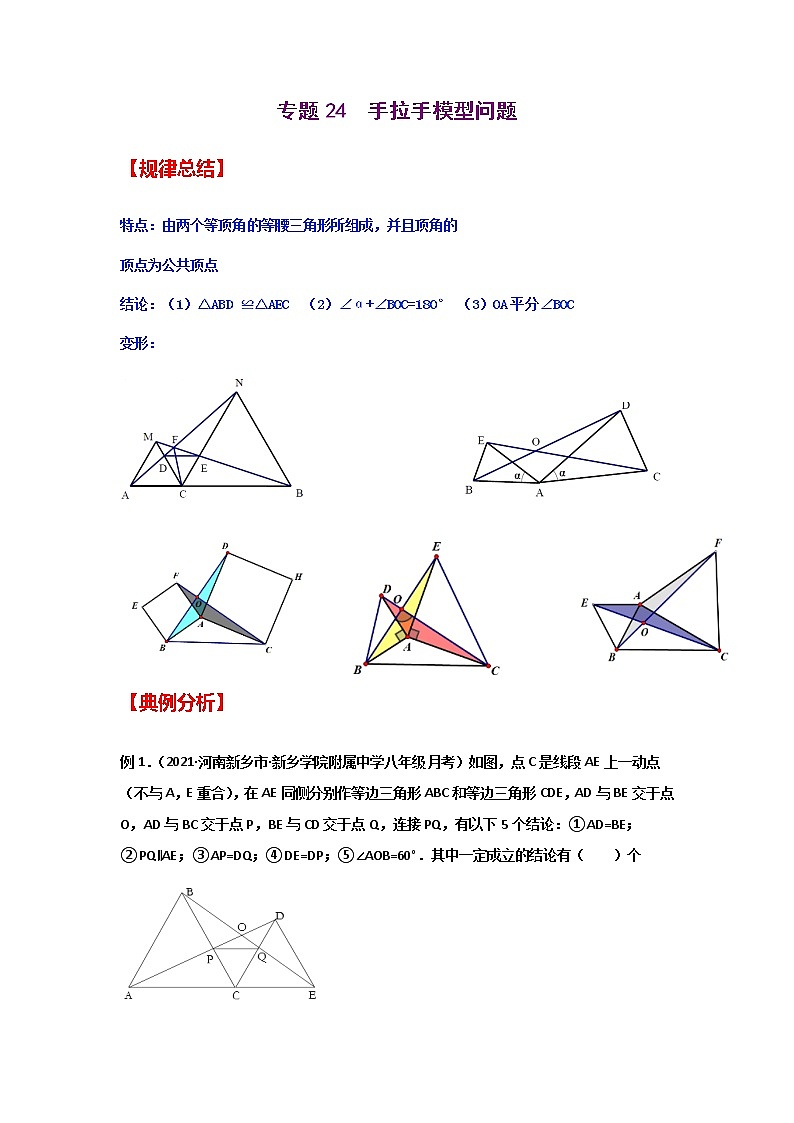
特点:由两个等顶角的等腰三角形所组成,并且顶角的
顶点为公共顶点
结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA平分∠BOC
变形:
【典例分析】
例1.(2021·河南新乡市·新乡学院附属中学八年级月考)如图,点C是线段AE上一动点(不与A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,有以下5个结论:①AD=BE;②PQ∥AE;③AP=DQ;④DE=DP;⑤∠AOB=60°.其中一定成立的结论有( )个
A.1 B.2 C.3 D.4
【答案】D
【分析】
①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
③由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故③正确;
②根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.
【详解】
①∵等边△ABC和等边△DCE,
∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60∘,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC,∠ACD=∠BCE,DC=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE;
故①正确;
③∵△ACD≌△BCE(已证),
∴∠CAD=∠CBE,
∵∠ACB=∠ECD=60°(已证),
∴∠BCQ=180°-60°×2=60°,
∴∠ACB=∠BCQ=60°,
在△ACP与△BCQ中,
∠CAD=∠CBE,AC=BC,∠ACB=∠BCQ=60°,
∴△ACP≌△BCQ(ASA),
∴AP=BQ;
故③正确;
②∵△ACP≌△BCQ,
∴PC=QC,
∴△PCQ是等边三角形,
∴∠CPQ=60∘,
∴∠ACB=∠CPQ,
∴PQ∥AE;
故②正确;
④∵AD=BE,AP=BQ,
∴AD−AP=BE−BQ,
即DP=QE,
∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,
∴DE≠QE,
则DP≠DE,故④错误;
⑤∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.
故⑤正确;
综上所述,正确的结论有:①②③⑤,错误的结论只有④,
故选D.
【点睛】
本题考查全等三角形的判定和性质,以及等边三角形的判定和性质,此图形是典型的“手拉手”模型,熟练掌握此模型的特点是解题的关键.
例2.(2020·武汉市二桥中学八年级月考)在中,,,,点D是直线BC上一动点,连接AD,在直线AD的右恻作等边,连接CE,当线段CE的长度最小时,则线段CD的长度为__________.
【答案】3
【分析】
以AC为边向左作等边三角形ACF,连接DF,先根据直角三角形中所对的直角边是斜边的一半求出BC的长,再由勾股定理求出AC的长,根据作的辅助线证明,则,当时,DF的长是最小的,即CE的长最小,求出此时的长即可.
【详解】
解:如图,以AC为边向左作等边三角形ACF,连接DF,
∵,,
∴,
∵,
∴,
∴,
∵是等边三角形,
∴,,
∵是等边三角形,
∴,,
∵,
∴,
在和中,
,
∴,
∴,
当时,DF的长是最小的,即CE的长最小,
∵,,
∴,,
∴当线段CE的长度最小时,则线段CD的长度为3.
故答案是:3.
【点睛】
本题考查线段最值问题,解题的关键是作辅助线构造全等三角形,以及掌握有角的特殊直角三角形的性质和等边三角形的性质.
例3.(2021·北京房山区·八年级期末)在中,,.
(1)如图1,点为边上一点,连接,以为边作,,,连接.直接写出线段与的数量关系为 ,位置关系为 .
(2)如图2,点为延长线上一点,连接,以为边作,,,连接.
①用等式表示线段,,之间的数量关系为 .
②求证:.
(3)如图3,点为外一点,且,若,,求的长.
【答案】(1),;(2)①,②见解析;(3).
【分析】
(1)由等腰直角三角形的性质得到,根据题意可知,即,再利用证明≌,可得到,,从而算出的度数,进而得到线段与的位置关系;
(2)①根据角度的运算得到,再利用证得≌,得到,再根据,等量代换即可求出答案;
②由①中≌,得到,,在根据等腰直角三角形的性质即可得出的度数,进而证得,根据勾股定理得到,,等量代换后得到,又因为,,代入即可得出答案;
(3)过点作,并且,连接,,得到是等腰直角三角形,由(2)得≌,得到,在中,通过勾股定理求出的长度,在中又由勾股定理得:,再根据,代入数据即可求出的长度.
【详解】
(1)在中,,,
,
,
,
即,
在和中
,
≌,
,,
,
.
故答案为:,.
(2)①,,
,
即,
在和中
,
≌,
,
,
.
故答案为:.
②证明:由①得:≌,
,,
和都是等腰直角三角形,
,
,
在和中,
由勾股定理得:,,
,
,,
,
即.
(3)过点作,并且,连接,,如图,
是等腰直角三角形,
,
,
,
由(2)中②可知,≌,
,
,,
,
在中,由勾股定理得:,
,
在中,由勾股定理得:,
,
.
【点睛】
本题考查了全等三角形的判定和性质,勾股定理,等腰三角形的性质,解题的关键是合理添加辅助线找出两个三角形全等.
【好题演练】
一、单选题
1.(2020·哈尔滨市第六十九中学校八年级期末)如图,在中,,点D、F是射线BC上两点,且,若,;则下列结论中正确的有( )
①;②;③;④
A.1个 B.2个 C.3个 D.4个
2.(2020·嵊州市三界镇中学八年级期中)如图,和都是等腰直角三角形,,连结交于点,连结交于点,连结.下列结论中:
(1),(2)是等腰直角三角形,(3),(4),(5).
正确的结论有( )
A.个 B.个 C.个 D.个
二、填空题
3.(2021·保定市莲池区贺阳外国语学校八年级期末)如图,在中,,,于点,于点.,连接,将沿直线翻折至所在的平面,得,连接.过点作交于点,则四边形的周长为________.
4.(2020·浙江锦绣育才教育科技集团有限公司九年级月考)如图,四边形ABCD为正方形.过正方形的顶点A和对角线的交点P,且与AB、AD分别交于点F,E.
(1)若,则______.
(2)若,的半径为,则______.
三、解答题
5.(2019·河南周口市·九年级二模)(1)(探索发现)
如图1,正方形ABCD中,点M、N分别是边BC、CD上的点,∠MAN=45°,若将△DAN绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为6,则正方形ABCD的边长为 .
(2)(类比延伸)
如图(2),四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M、N分别在边BC、CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.
(3)(拓展应用)
如图3,四边形ABCD中,AB=AD=10,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,△ABM是等边三角形,AM⊥AD,DN=5(﹣1),请直接写出MN的长.
6.(2020·鄱阳县第二中学八年级月考)如图1,在△ABC中,AC=BC,∠ACB=90°,CE与AB相交于点D,且BE⊥CE,AF⊥CE,垂足分别为点E,F.
(1)若AF=5,BE=2,求EF的长;
(2)如图2,取AB的中点G,连接FG,EG,求证:FG=EG.
中考经典几何模型与最值问题 专题01 截长补短模型证明问题: 这是一份中考经典几何模型与最值问题 专题01 截长补短模型证明问题,文件包含专题01截长补短模型证明问题教师版docx、专题01截长补短模型证明问题学生版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案(全国通用): 这是一份专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案(全国通用),文件包含专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案解析版docx、专题24函数与菱形存在性问题-中考数学压轴大题之经典模型培优案原卷版docx等2份试卷配套教学资源,其中试卷共94页, 欢迎下载使用。
中考经典几何模型与最值问题 专题05 手拉手模型构造全等三角形: 这是一份中考经典几何模型与最值问题 专题05 手拉手模型构造全等三角形,文件包含专题05手拉手模型构造全等三角形教师版docx、专题05手拉手模型构造全等三角形学生版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。












