专题54 与二次函数有关的综合问题（2）-2021年中考数学二轮复习经典问题专题训练

专题54  与二次函数有关的综合问题（2）

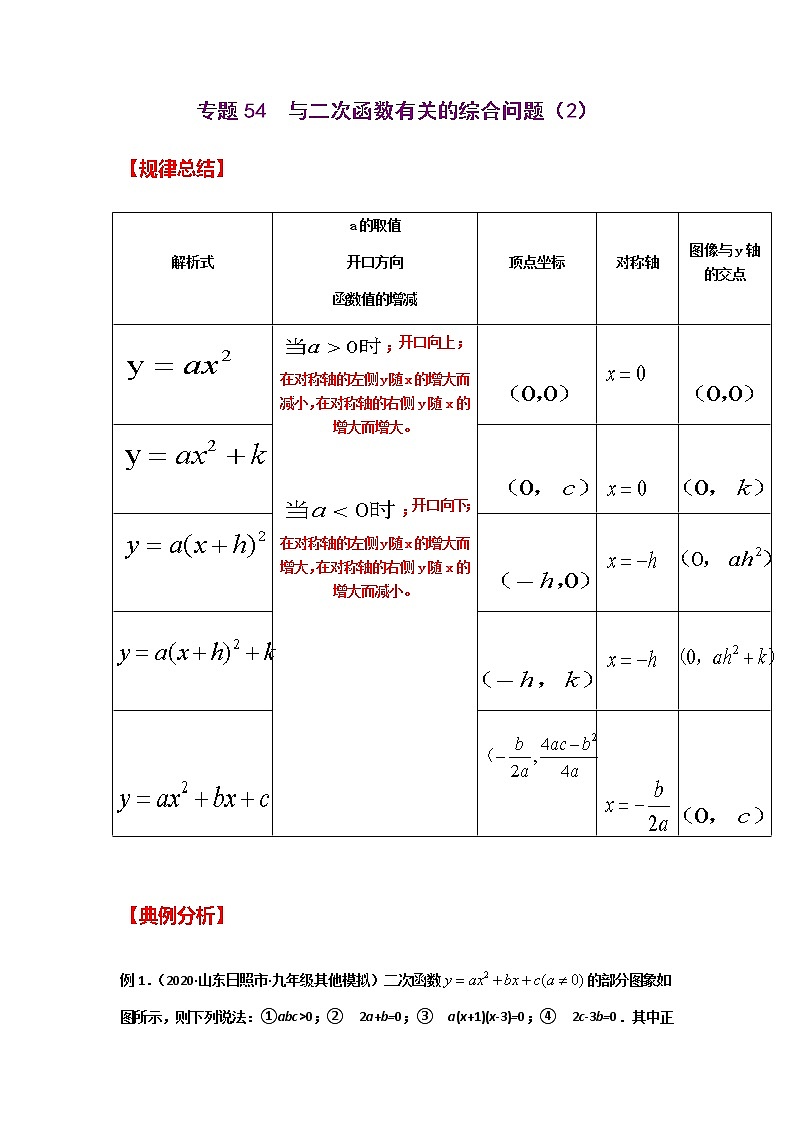
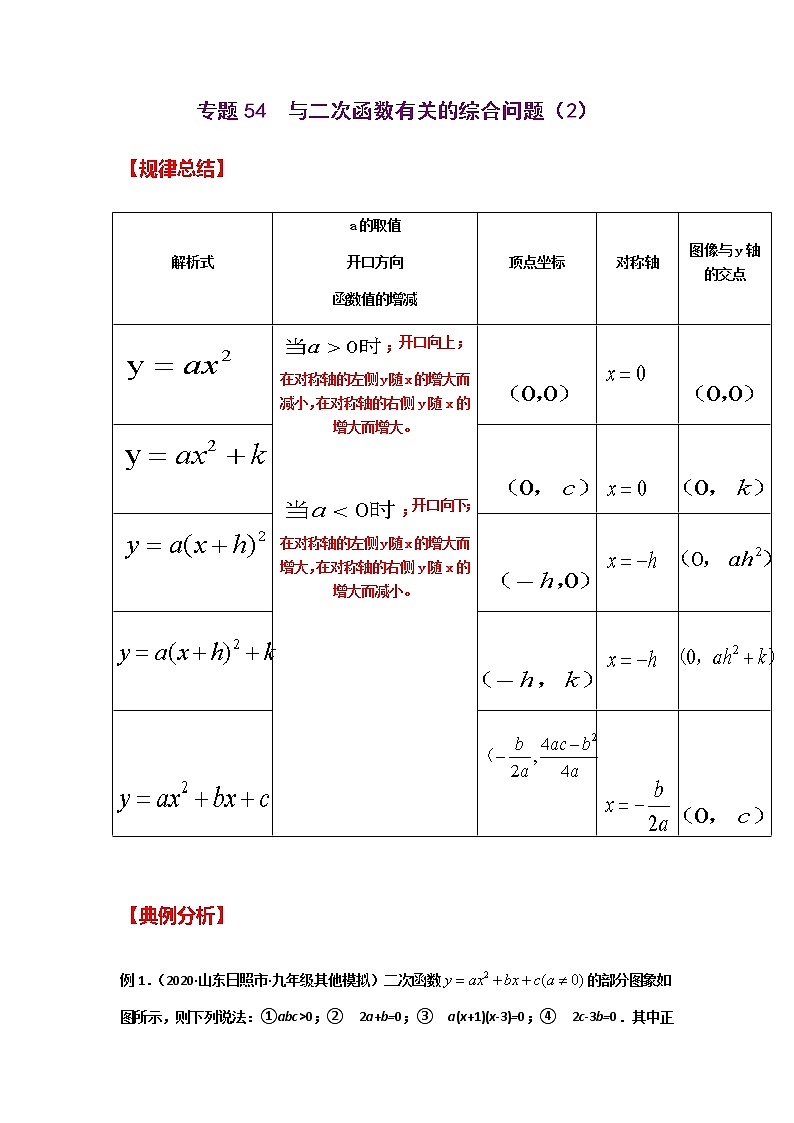
【规律总结】

【典例分析】

例1．（2020·山东日照市·九年级其他模拟）二次函数的部分图象如图所示，则下列说法：①abc>0；②　2a+b=0；③　a(x+1)(x-3)=0；④　2c-3b=0．其中正确的个数为（　　）

A．1 B．2 C．3 D．4

【答案】B

【分析】

先根据二次函数的对称性补全函数图像，由函数的开口方向，对称轴以及与y轴的交点确定a，b，c的符号，从而判断①；根据对称轴的位置判断②；根据函数的解析式判断③；根据二次函数图象与x轴的交点判断④．

【详解】

解：如图，由抛物线过，对称轴为 根据对称性得到抛物线的图像经过

①图象开口向下， ∴a＜0，

与y轴交于正半轴， ∴c＞0，

对称轴在y轴右侧， ∴b＞0，

则abc＜0，故①错误；

②对称轴 解得，2a+b=0，故②正确；

③由抛物线与轴的交点坐标为：，

所以函数解析式为：y=a（x+1）（x-3），

所以y的值是不断变化的，故③错误；

④∵抛物线与x轴交于（-1，0）和（3，0），

∴a-b+c=0，9a+3b+c=0，

 两式相加得，10a+2b+2c=0，

又b=-2a，

，

∴2c-3b=0，故④正确．

故选：．

【点睛】

本题考查的是图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及掌握二次函数的交点式是解题的关键．

例2．（2018·华中师范大学第一附属中学光谷分校九年级月考）已知抛物线与轴交于点、，与轴交于点，则能使为等腰三角形的抛物线的条数是________．

【答案】4.

【解析】

整理抛物线解析式，确定出抛物线与x轴的一个交点A和y轴的交点C，然后求出AC的长度，再分：

①k＞0时，点B在x轴正半轴时，分AC=BC、AC=AB、AB=BC三种情况求解；

②k＜0时，点B在x轴的负半轴时，点B只能在点A的左边，只有AC=AB一种情况列式计算即可．

解：y=k（x+1）（x﹣）=（x+1）（kx﹣3），

所以，抛物线经过点A（﹣1，0），C（0，﹣3），

AC==，

点B坐标为（，0），

①k＞0时，点B在x正半轴上，

若AC=BC，则=，解得k=3，

若AC=AB，则+1=，解得k==，

若AB=BC，则+1=，解得k=；

②k＜0时，点B在x轴的负半轴，点B只能在点A的左侧，

只有AC=AB，则﹣1﹣=，解得k==，

所以，能使△ABC为等腰三角形的抛物线共有4条．

故答案是：4．

例3．（2021·汝南县清华园学校九年级期末）如图，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于点，已知，，连接，点是抛物线上的一个动点，点是对称轴上的一个动点．

（1）求该抛物线的函数解析式．

（2）当的面积为8时，求点的坐标．

（3）若点在直线的下方，当点到直线的距离最大时，在抛物线上是否存在点，使得以点，，，为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，请说明理由．

【答案】（1）；（2）点坐标为，或，或；（3）存在；，或，或．

【分析】

（1）利用待定系数法可求解析式；
（2）设点P（p，p2-2p-3），由三角形的面积公式可求解；
（3）当有最大值时，点到直线的距离最大，据此先求点P坐标；然后分三种情况讨论：若为边，为边时，则与互相平分；若为边，为边时，则与互相平分；若为对角线，则与互相平分．利用平行四边形对角线互相平分的性质可求解．

【详解】

解：（1）抛物线经过点，，

，

解得：，

抛物线的解析式为；

（2）抛物线与轴交于，两点，

，

，，

点，

，

设点，

的面积为8，

，

或，

，，，

点坐标为，或，或；

（3）如图1，过点作轴，交于，

点，，

直线的解析式为，

设点，则点，

，

，

当时，有最大值，即点到直线的距离最大，

此时点，，

设点，点，

若为边，为边时，则与互相平分，

，

，

点，，

若为边，为边时，则与互相平分，

，

，

点，，

若为对角线，则与互相平分，

，

，

点，

综上所述：点坐标为，或，或．

【点睛】

本题是二次函数综合题，考查了待定系数法求解析式，二次函数的性质，平行四边形的性质，三角形的面积公式等知识，利用分类讨论思想解决问题是本题的关键．

【好题演练】

一、单选题

1．（2019·湖南长沙市·八年级期末）已知二次函数y＝ax2+bx+c(a≠0)的图象如图所示，则下列结论：①a+b+c＞0，②方程ax2+bx+c＝0两根之和大于零，③y随x的增大而增大，④一次函数y＝x+bc的图象一定不过第二象限，其中正确的个数是（   ）

A．4个 B．3个 C．2个 D．1个

2．（2020·山东德州市·九年级二模）二次函数的函数图象如图，点位于坐标原点，点在轴的正半轴上，点在二次函数位于第一象限的图象上，，，，…都是直角顶点在抛物线上的等腰直角三角形，则的斜边长为(　　)

A．20 B． C．22 D．

二、填空题

3．（2020·全国九年级课时练习）如图，在平面直角坐标系中，过点作x轴的垂线，分别交抛物线与直线交于点A，B，以线段为对角线作菱形，使得，则菱形的面积最小值为______．

4．（2020·德惠市第九中学）研究抛物线的性质时，将一个直角三角板的直角顶点置于平面直角坐标系的原点O，两直角边与该抛物线交于A，B两点（如图），将三角板绕点O旋转任意角度时发现，交点A，B所连线段总经过一个固定的点，则该定点的坐标是_____．

三、解答题

5．（2021·山东省枣庄市第二十九中学九年级期末）如图，已知一次函数与抛物线都经过轴上的点和轴上的点．

（1）求抛物线的解析式；

（2）若抛物线的顶点为，试求出点的坐标和△的面积；

（3）是线段上的一点，过点作轴，与抛物线交于点，若直线把△分成的两部分面积之比为1∶3，请求出点的坐标．

6．（2020·浙江杭州市·八年级其他模拟）如图，在平面直角坐标系中，等腰的斜边在x轴上，．抛物线过点O，A，B．

（1）求该抛物线的解析式；

（2）点是线段上一动点，过点P作y轴的平行线，交直线于点E，交抛物线于点F，以为一边，在的右侧作矩形．

①若，求矩形面积的最大值；

②若，矩形与等腰重叠部分为轴对称图形，求m的取值范围．