初中数学人教版八年级下册18.1.2 平行四边形的判定教学课件ppt

这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定教学课件ppt，共25页。PPT课件主要包含了平行四边形，学习目标，还有其他方法吗，两组对边分别平行，∠BAD∠DCB，∠ABC∠CDA，四边形AE，∵ADBC，∴∠FDO∠EBO，∴ABDC等内容，欢迎下载使用。

判定1两组对边分别平行的四边形是平行四边形.数学语言∵ AB//CD、AD//BC∴四边形ABCD是平行四边形判定2两组对边分别相等的四边形是平行四边形.数学语言∵ AB=CD、AD=BC∴四边形ABCD是平行四边形判定3两组对角分别相等的四边形是平行四边形.数学语言∵ ∠A=∠C，∠B=∠D∴四边形ABCD是平行四边形
探索并证明平行四边形的判定定理.能熟练运用平行四边形的判定定理去计算 和证明.
思考 如图，将两根木条的中心重叠在一起，用小钢钉固 定住，然后用橡皮筋连接木条的顶点，做成一个四边形. 猜 一猜，这个四边形是平行四边形吗？你能证明吗？
知识点：平行四边形的判定
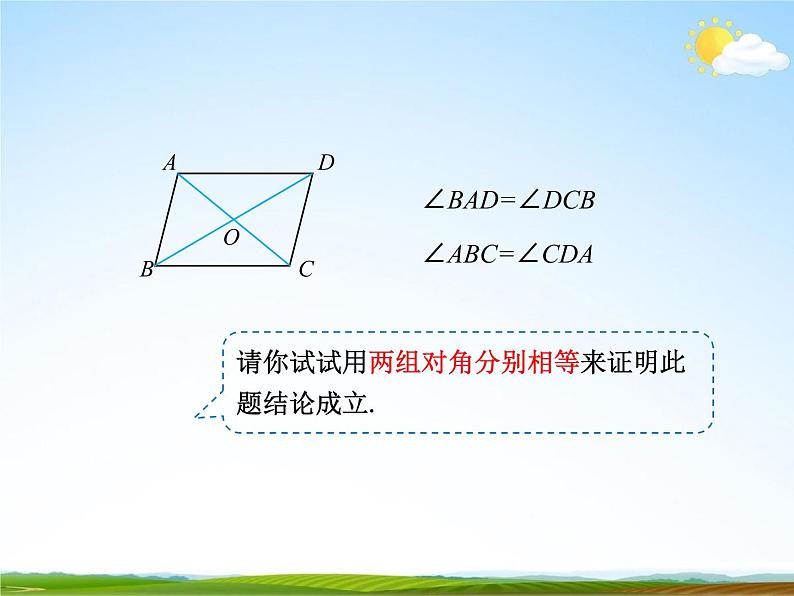
例如图，在四边形 ABCD 中，AC，BD 相交于点 O，且 OA=OC，OB=OD. 求证：四边形 ABCD 是平行四边形.
解析：根据题意，有相等的边 和相等的角，所以利用全等三
角形和平行线的判定来证明.
证明：∵ OA=OC，∠AOD=∠COB，OB=OD
∴ 四边形 ABCD 是平行四边形.
∴ △AOD ≌△COB
∴ ∠OAD=∠OCB∴ AD//BC，同理可得 AB//DC
证明：∵ OA=OC，∠AOB=∠COD，OB=OD
同理可得 AD=BC∴ 四边形 ABCD 是平行四边 形.
∴ △AOB≌△COD两组对边分别相等∴ AB=CD
请你试试用两组对角分别相等来证明此 题结论成立.
平行四边形的判定4：对角线互相平分的四边形是平行四边形.
数学语言：∵ OA=OC、OB=OD∴ 四边形ABCD是平行四边形
通过对上面例题的证明，你能得出什 么判定方法呢？
例3如图，ABCD 的对角线 AC、BD 相交于点 O，E、F
是 AC上的两点，并且 AE=CF. 求证：四边形 BFDE 是平行
证明：∵ 四边形 ABCD 是平行四边形∴ AO=CO， BO=DO∵ AE=CF∴ AO-AE=CO-CF， 即EO=FO 又 BO=DO∴ 四边形 BFDE 是平行四边形
训练1.如图，线段AB，CD相交于点O，且图上各点把线段AB，CD四等分，这些点可以构成 4个平行四边形．D
2.如图， 在平行四边形 ABCD 中，EF 过对角线 BD 的中 点 O. 求证：四边形 BFDE 是平行四边形.
证明：∵四边形 ABCD 是平行四边形∴OB=OD，AD//BC
∵ ∠FDO=∠EBO，OD=OB， ∠FOD=∠EOB∴△FDO≌△EBO，OF=OE∴四边形 BFDE 是平行四边形
1.如图， E、F 是平行四边形 ABCD 的对角线 AC 上的两点， 并且 BE//DF. 求证：四边形 BFDE 是平行四边形.
解析：连接BD，利用三角形的全等 来得到边、角之间的关系，进而证 明该四边形是平行四边形.
证明：连接 BD，交 AC 于点 O
∵四边形 ABCD 是平行四边形∴OA=OC， OB=OD∵BE//DF∴∠EBO=∠FDO
∵在△EBO和△FDO中，∠EBO=∠FDO，OB=OD∠EOB=∠FOD∴△EBO≌△FDO(ASA) ， EO=FO∵EO=FO，BO=DO∴四边形 BFDE 是平行四边形
2.如图， 平行四边形 ABCD 的对角线 AC、BD 相交于点O， 点E、F、G、H分别是OA、OB、OC、OD的中点.求证：四 边形 EFGH 是平行四边形.
解析：根据题意可知， OA=OC、 OB=OD，利用中点的性质，可 以得到OE=OG、OF=OH.
证明：∵四边形 ABCD 是平行四边
∴OA=OC， OB=OD∵ E、F、G、H分别是OA、OB、 OC、OD的中点∴OE=OG， OF=OH∴四边形 EFGH 是平行四边形
3.如图，O 是ABCD 对角线 AC 的中点，过点 O 的直 线ME、NF 分别交ABCD的边于点M、E、N、F. 求证： MN//FE且MN=FE.
解析：根据题意，可以利用平行四 边形对角线的性质和全等三角形来 证明四边形 MNEF 是平行四边形.
证明：∵四边形ABCD是平行四边形
∴∠MAO=∠ECO，∠AMO=∠CEO又O是 AC 的中点∴ AO=CO∴△AMO≌△CEO，MO=EO 同理可得 NO=FO∴四边形 MNEF 是平行四边形∴ MN//FE 且 MN=FE
对角线互相平分的四边形 是平行四边形.
∵ OA=OC、OB=OD∴四边形ABCD是平行四边形
证明：连接BD交AC于点O， 则∠DON =∠BOM，OD=OB，∵BM⊥AC，DN⊥AC，∴∠OND =∠OMB = 90°，∴△DON≌△BOM，∴ON=OM，∴四边形BMDN是平行四边形．
1.如图所示，AC是ABCD的一条对角线，BM⊥AC于点
M，DN⊥AC于点N，求证：四边形BMDN是平行四边形.
2.如图，点 D 为三角形 ABC 的边 AB上一点，DF 交 AC 于 点E，且 AE=CE，FC//AB. 求证：四边形 ADCF 是平行四边 形.
∴四边形ADCF是平行四边形
解： ∵FC//AB∴∠ADE=∠CFE∵ 在△ADE和△CFE中， ∠ADE=∠CFE ，∠AED=∠CEF，AE=CE
∴△ADE≌△CFE∴DE=FE∵AE=CE， DE=FE
3.如图，已知 E，F 是四边形 ABCD 的对角线 BD 的三等分 点，CE，CF 的延长线分别平分 AB，AD. 求证：四边形 ABCD 是平行四边形．B
证明：连接AC交BD于点O，连接AE，AF∵点G是AB的中点，BE=EF
∴GE是△ABF的一条中位线，∴GE∥AF，即CE∥AF，
同理可得 CF∥AE，
∴四边形AFCE是平行四边形．
∴OA=OC，OE=OF，又∵BE=DF，∴OB=OD，∴四边形ABCD是平行四边形．
请完成课本后习题第2题。