人教版数学中考复习《函数的综合应用》教学课件ppt课件

这是一份人教版数学中考复习《函数的综合应用》教学课件ppt课件，共19页。PPT课件主要包含了问题1，问题2，问题3等内容，欢迎下载使用。

y与x之间的函数关系式，并画出该函数图象 的草图；
（2）若镜面玻璃的长与宽的比是2∶1，其周 长是l m，求l与x之间的函数关系式，并画出 该函数图象的草图；
（3）若镜面玻璃的长与宽的比是2∶ 1，其面 积是s m2，求s与x之间的函数关系式，并画出 该函数图象的草图；
如图，是一块长方形的镜面玻璃，玻璃的宽是 x m．（1）若镜面玻璃的长是y m，面积为1m2，求
上面的问题，你能比较它们的不同之处吗？ 请做出解释.你是如何得到函数关系式的？在实际问题中，你所得到的函数的自变量 有什么要求？
现有一块长方形的镜面玻璃，玻璃的宽是 x m，在 它的四周镶上与它的周长相等的边框，制成一面镜 子．镜子的长与宽的比是2∶ 1，已知边框的价格是 每米10元．（1）若制作边框的费用为y元，求y与x之间的函 数关系式；解：因为镜子的长与宽的比是2∶1，玻璃的宽是x m， 所以镜子的长是2 x m ．y =10·2(2x+x ) = 60 x ．
（2）若镜面玻璃的价格是每平方米50元，另外 制作这面镜子还需加工费10元．①求制作这面镜子的总费用w(单位：元)与x之 间的函数关系式；
②如果制作这面镜子共花了17元，求这面镜子 的长和宽 ．解： ① w =50·2x2 + 60 x +10 = 100x2+ 60x +10 ；② 当w =17时，100x2+ 60x +10 = 17，解得 x = 0.1， x = -0.7（不合题意，舍去） 所以这面镜子的长是0.2m，宽是0.1m .
本题你是如何得到函数关系式的？说一说函数与方程的联系.
该厂生产了一种成本为20元∕个的小镜子投放市场进行试 销．经过调查，得到如下数据：
（1）认真分析上表中的数据，用所学过的一次函数、二次函 数、反比例函数的知识确定一个满足这些数据的y（个）与x（元∕个）之间的关系式；思考（1）你是如何判断y与x之间的关系是哪一种函数关系的？
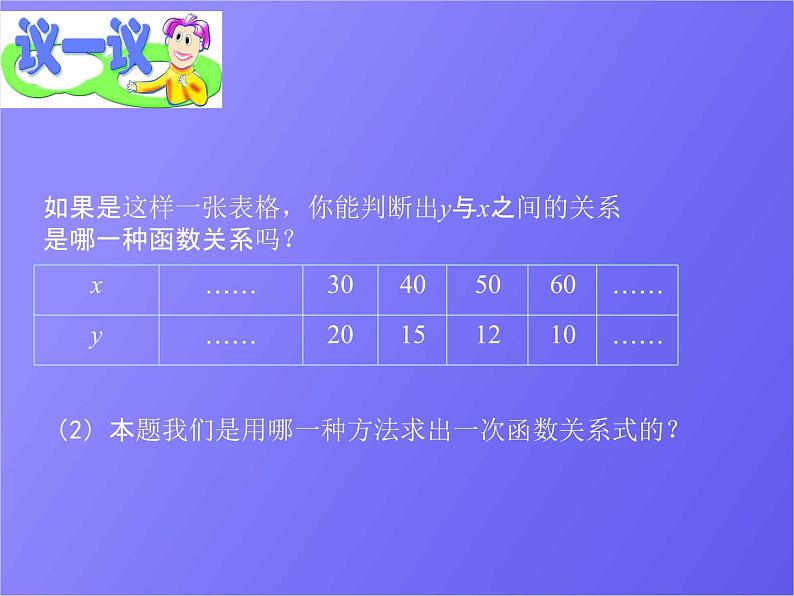
如果是这样一张表格，你能判断出y与x之间的关系 是哪一种函数关系吗？
（2）本题我们是用哪一种方法求出一次函数关系式的？
（2）当销售单价定为多少时，该厂试销这种镜子每天获得的 总利润最大？最大利润是多少？（总利润=每个镜子的利润× 销售量）（3）当地物价部门规定，这种镜子的销售单价最高不能超 过45元/个，那么销售单价定为多少时，该厂试销这种镜子 每天获得的利润最大？
对于第2个问题，我们是用什么方法求出二次函数关系 式的？它与第1个问题所求出的一次函数有什么联系？通过解决问题2和问题3，对于求二次函数的最大（小） 值有没有什么需要注意的?
某校科技小组进行野外考察，途中遇到一片的烂泥湿 地．为了人员和设备安全迅速地通过这片湿地，他们沿着 前进路线铺了若干块大小不同的木板，构筑成一条临时通 道．下图是小明通过临时通道时踩在大小不同的木板上对 烂泥湿地的压强的图象．已知当压力不变时，木板对地面 的压强p(Pa)是木板面积S(m2)的反比例函数.请直接写出p与S之间的关 系式和自变量取值范围；当木板面积为0.2 m2时， 压强是多少？
2．某宾馆客房部有60个房间供游客居住，当每个房 间的定价为每天200元时，房间可以住满．当每个房 间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．设每个房间每天的定价增加x元．求：(1)房间每天的入住量y(间)关于 x(元)的函数关系式． (2)该宾馆每天的房间收费z(元)关于x(元)的函数关系 式．(3)该宾馆客房部每天的利润w(元)关于x(元)的函数 关系式；当每个房间的定价为每天多少元时， w有 最大值？最大值是多少？
回顾解决问题的过程，思考函数在解决问题过程 中的作用；回顾建立函数模型的过程，思考如何求出函数关 系式；回顾在解决问题过程中遇到的困难和出现的错误， 思考在用函数解决实际问题时有哪些需要引起重视 的地方.
红星公司生产的某种时令商品每件成本为20元，经过市场调研发现， 这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表：
未来40天内，前20天每天的价格y1(元/件)与时间t(天)的函数关系式为 y1=0.25t+25(1≤t ≤20且为整数)，后20天每天的价格y2(元/件)与时间t(天) 的函数关系式为 y2=-0.5t+40(21 ≤ t ≤40且为整数)．下面我们就来研究销 售这种商品的有关问题：认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函 数的知识确定一个满足这些数据的m(件)与(天)之间的关系式；请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？ (3)在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润 (a＜4)给希望工程．公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t(天)的增大而增大，求a的取值范围．
随着销量的增加，制造厂制作镜面玻璃的某种原料每天的需 求量也在增加，其需求量y(千克)与生产时间x(天)之间的关系 如折线图所示.这些原料在第30天后每天的需求量比前一天增
加100千克.分别求出x≤30和x≥30时，y与x之间的关系式；如果这些原料每天的需求 量大于或等于4000千克时需要 进行加班生产，那么应从第几 天开始进行加班生产？
本题我们是用哪种方法求出一次函数关 系式的？对于第2个问题，你是怎样选择函数关 系式帮助你解决问题的？为什么这样选择？ (3)你觉得解决这类(含有两个一次函数关系) 实际问题需要注意什么？