人教版2021年八年级下册期末复习培优训练试题 （word版，含详解）

这是一份人教版2021年八年级下册期末复习培优训练试题 （word版，含详解），共18页。试卷主要包含了已知函数y＝kx，点P等内容，欢迎下载使用。


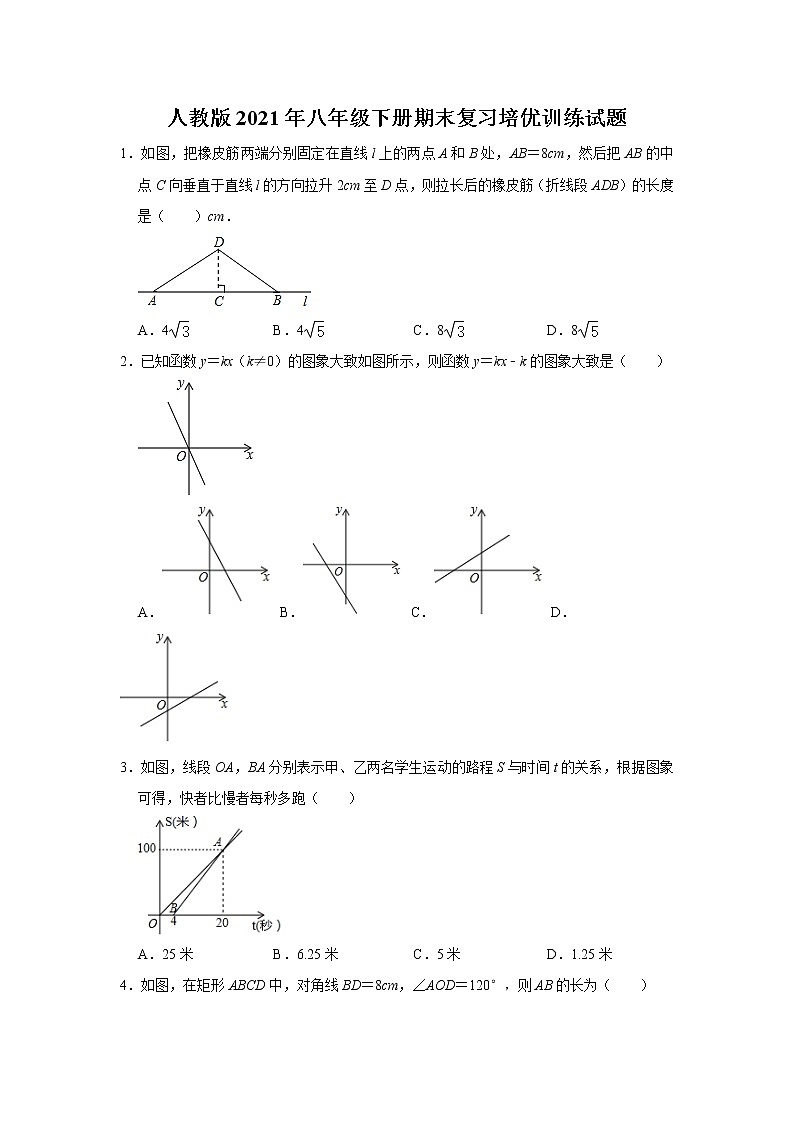
A．4B．4C．8D．8
2．已知函数y＝kx（k≠0）的图象大致如图所示，则函数y＝kx﹣k的图象大致是（ ）
A． B． C． D．
3．如图，线段OA，BA分别表示甲、乙两名学生运动的路程S与时间t的关系，根据图象可得，快者比慢者每秒多跑（ ）
A．25米B．6.25米C．5米D．1.25米
4．如图，在矩形ABCD中，对角线BD＝8cm，∠AOD＝120°，则AB的长为（ ）
A．cmB．2cmC．2 cmD．4cm
5．如图，一次函数y1＝x+b与一次函数y2＝kx+4的图象相交于点P（2，﹣2），则关于x的不等式x+b＞kx+4的解集是（ ）
A．x＞﹣2B．x＜﹣2C．x＜2D．x＞2
6．点P（x，y）在第一象限内，且x+y＝6，点A的坐标为（4，0）．设△OPA的面积为S，则下列图象中，能正确反映S与x之间的函数关系式的是（ ）
A．B．C．D．
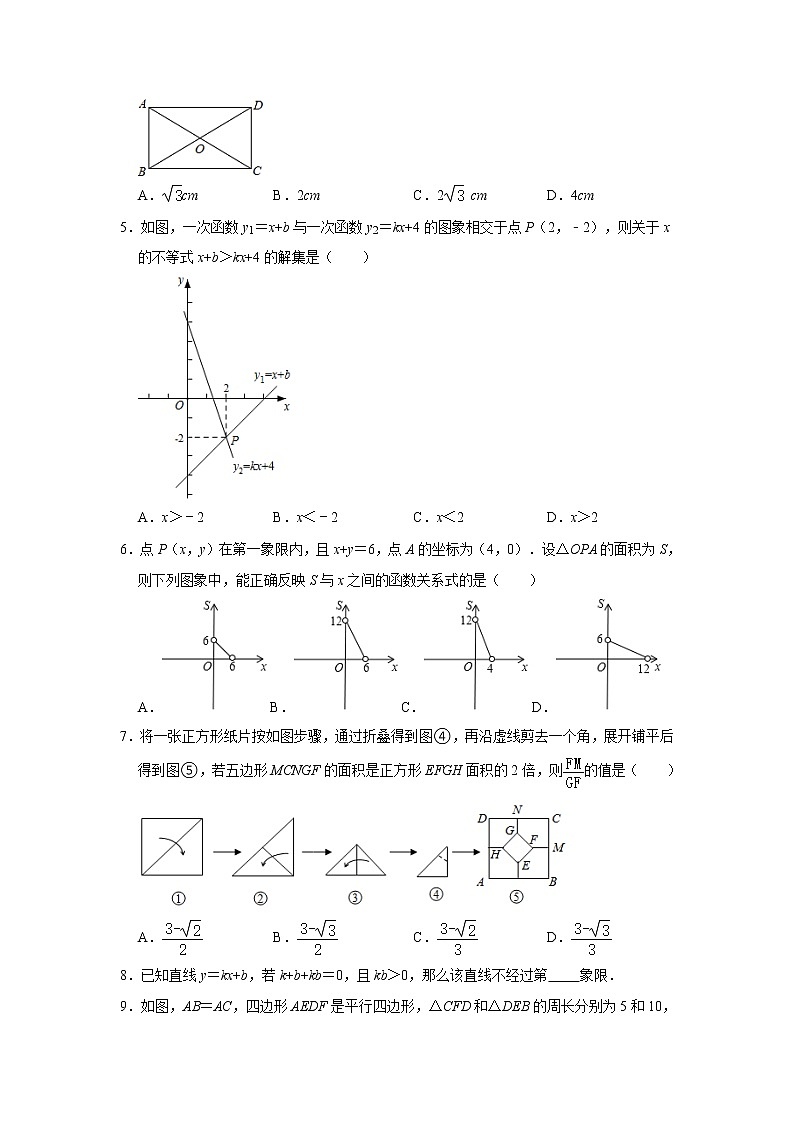
7．将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，若五边形MCNGF的面积是正方形EFGH面积的2倍，则的值是（ ）
A．B．C．D．
8．已知直线y＝kx+b，若k+b+kb＝0，且kb＞0，那么该直线不经过第 象限．
9．如图，AB＝AC，四边形AEDF是平行四边形，△CFD和△DEB的周长分别为5和10，则△ABC的周长是 ．
10．如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边的正方形EFGH的周长为 ．
11．如图，△ACB和△ECD都是等腰直角三角形，且直角顶点均为点C，点A是DE边上一动点，若DE＝2，则下列结论：
①∠DCB＝∠DAB；②CE＞CB；③AC2﹣AD2＝AE2﹣AC2；④S△ACB的最小值为．
其中正确的结论是 ．（填写所有正确结论的序号）
12．已知三角形一边上的中线，与三角形三边有如下数量关系：三角形两边的平方和等于第三边一半的平方与第三边中线平方之和的2倍．即：如图1，在△ABC中，AD是BC边上的中线，则有AB2+AC2＝2（BD2+AD2）．请运用上述结论，解答下面问题：如图2，点P为矩形ABCD外部一点，已知PA＝PC＝3，若PD＝1，则AC的取值范围为 ．
13．已知矩形ABCD的对角线交于点O，△AOB的周长为12，OA＝x，AB＝y．
（1）当x＝4时，求y的值；
（2）写出y关于x的函数解析式，并写出自变量x的取值范围；
（3）如图，在平面直角坐标系中，画出（2）中的函数图象．
14．A城有肥料200t，B城有肥料300t，现要把这些肥料全部运往C、D两乡．从A城运往C，D两乡肥料费用分别为20元/t和25元/t；从B城运往C，D两乡运肥料的费用分别为15元/t和24元/t．现C乡需要肥料240t，D乡需要肥料260t．
设A城运往C乡xt，请解答下列问题：
（1）根据题意，填写下列表格：
（2）设总运费为W（元），求出W（元）与x（吨）的函数关系式，并写出自变量x的取值范围．
（3）求怎么调运可使总运费最少？最少为多少元？
15．如图，直线y1＝x+3与直线y2＝mx+交于点M（﹣1，2），与x轴分别交于点A，B，与y轴分别交于C，D．
（1）根据图象写出方程组的解是 ．
（2）根据函数图象写出不等式x+3≤mx+的解集 ．
（3）求直线AC，直线BD与x轴围成的△ABM的面积．
16．如图，在平面直角坐标系中，直线l1：y＝﹣x+6分别与x轴、y轴交于点B、C．且与直线l2：y＝x交于点A．
（1）请写出A（ ， ），B（ ， ），C（ ， ）．
（2）若D是线段OA上的一点，且△COD的面积为12，求直线CD的函数表达式．
（3）在（2）的条件下，设P是射线CD上的点，在平面内存在点Q，使以O、C、P、Q为顶点的四边形是菱形，请直接写出Q点的坐标．
17．如图，在平面直角坐标系xOy中，已知直线l1：y＝x﹣2和直线l2：y＝2x﹣4相交于点A．
（1）已知点P（1﹣t，9﹣3t），求证：无论t为何值，点P总在直线y＝3x+6上；
（2）直线y＝3x+6分别与x轴、y轴交于B、C两点，平移线段BC，使点B、C的对应点M、N分别落在直线l1和l2上，请你判断四边形BMNC的形状，并说明理由；
（3）在（2）问的条件下，已知直线y＝mx﹣6m+8 把四边形BMNC的面积分成1：3两部分，求m的值．
18．已知菱形ABCD的边长为2，∠ABC＝60°，对角线AC、BD相交于点O．点M从点B向点C运动（到点C时停止），点N为CD上一点，且∠MAN＝60°，连接AM交BD于点P．
（1）求菱形ABCD的面积；
（2）如图1，过点D作DG⊥AN于点G，若BM＝4﹣2，求NG的长；
（3）如图2，点E是AN上一点，且AE＝AP，连接BE、OE．试判断：在运动过程中，BE+OE是否存在最小值？若存在，请求出；若不存在，请说明理由．
参考答案
1．解：∵把AB的中点C向垂直于直线l的方向拉升，
∴DC是AB的垂直平分线，
∵AB＝8cm，
∴AC＝BC＝4cm，AD＝BD，
在Rt△ADC中：AD＝＝＝2，
∴拉长后的橡皮筋（折线段ADB）的长度是：2×2＝4，
故选：B．
2．解：因为正比例函数y＝kx（k≠0）的图象经过第二、四象限，
所以k＜0，
所以一次函数y＝kx﹣k的图象经过一、二、四象限，
故选：A．
3．解：由图象可得，
快者的速度为：100÷（20﹣4）＝6.25（米/秒），
慢者的速度为：100÷20＝5（米/秒），
快者比慢者每秒多跑6.25﹣5＝1.25（米/秒），
故选：D．
4．解：∵∠AOD＝120°，
∴∠AOB＝60°，
∵四边形ABCD是矩形，
∴AC＝BD，AO＝OC，BO＝OD＝cm，
∴AO＝BO＝4cm，
∴△ABO是等边三角形，
∴AB＝AO＝4cm，
故选：D．
5．解：∵一次函数y1＝x+b与一次函数y2＝kx+4的图象相交于点P（2，﹣2），
∴当x＞2时，x+b＞kx+4，
即关于x的不等式x+b＞kx+4的解集是x＞2．
故选：D．
6．解：∵点P（x，y）在第一象限内，且x+y＝6，点A的坐标为（4，0），
∴S＝＝2y＝2（6﹣x）＝﹣2x+12，0＜x＜6，
∴0＜S＜12，
故选：B．
7．解：如图，连接HF，直线HF与AD交于点P，
∵五边形MCNGF的面积是正方形EFGH面积的2倍，
设正方形EFGH与五边形MCNGF的面积为x2，2x2，
∴GF2＝x2，
∴GF＝x，
∴HF＝x，
由折叠可知：
正方形ABCD的面积为：x2+4×2x2＝9x2，
∴PM2＝9x2，
∴PM＝3x，
∴FM＝PH＝（PM﹣HF）＝（3x﹣x）＝（3﹣）x，
∴＝＝．
故选：A．
8．解：∵k+b+kb＝0，且kb＞0，
∴k+b＝﹣kb＜0，k和b同号，
∴k＜0，b＜0，
∴直线y＝kx+b经过第二、三、四象限，不经过第一象限，
故答案为：一．
9．解：∵四边形AEDF是平行四边形，
∴DE＝AF，DF＝AE，
∵△CFD和△DEB的周长分别为5和10，
∴CF+DF+CD＝5，DE+EB+DB＝10，
∴CF+AE+CD＝5，AF+EB+DB＝10，
∴△ABC的周长＝CF+AF+AE+EB+BD+CD＝15．
故答案为：15．
10．解：∵正方形ABCD的面积为1，
∴BC＝CD＝＝1，∠BCD＝90°，
∵E、F分别是BC、CD的中点，
∴CE＝BC＝，CF＝CD＝，
∴CE＝CF，
∴△CEF是等腰直角三角形，
∴EF＝CE＝，
∴正方形EFGH的周长＝4EF＝4×＝2 ；
故答案为2．
11．解：如图，∵△ACB和△ECD都是等腰直角三角形，且直角顶点均为点C，
∴∠E＝∠EDC＝∠CAB＝∠ABC＝45°，∠ECD＝∠ACB＝90°，CE＝CD，CA＝CB，
∵∠DOB＝∠DAB+∠EDC＝∠DCB+∠ABC，
∴∠DCB＝∠DAB，
故①正确；
当A和E或D重合时CE＝CB，
点点A不和点E或点D重合时，
∵∠EAC＞∠ECD＝∠E，
∴CE＞CA，
∴CE＞CB，
综上，CE≥CB，
故②不正确；
连接DB，
∵∠ECD＝∠ACB＝90°，
∴∠ECA＝∠DCB，
∵CE＝CD，CA＝CB，
∴△EAC≌△DBC（SAS），
∴AE＝BD，∠E＝∠CDB＝45°，
∴∠EDB＝90°，
∴AD2+DB2＝AB2，
∵2AC2＝AC2+BC2＝AB2，
∴AD2+AE2＝2AC2，
即AC2﹣AD2＝AE2﹣AC2，故③正确；
∵S△ACB＝AC•BC＝AC2＝×2AC2＝（AD2+AE2），DE＝2，
∴S△ACB＝[AD2+（2﹣AD）2]
＝（2AD2﹣4AD+4）
＝（AD2﹣2AD+2）
＝（AD﹣1）2+
∴S△ACB的最小值为，故④正确．
故答案为①③④．
12．解：如图，连接BD交AC于O，连接PO，
∵四边形ABCD是矩形，
∴AC＝BD，AO＝CO＝BO＝DO，
∵PO是△ACP的中线，也是△PBD的中线，
∴PA2+PC2＝2（AO2+PO2），PB2+PD2＝2（PO2+OD2），
∴PA2+PC2＝PB2+PD2，
∴9+9＝1+PB2，
∴PB＝，
在△PBD中，﹣1≤BD≤+1，
∴﹣1≤AC≤+1，
当点P在AD上时，CD＝＝＝2，
∴AC＝＝＝2，
故答案为：﹣1≤AC＜2．
13．解：（1）依题意有2x+y＝12，
当x＝4时，8+y＝12，
解得y＝4；
（2）∵2x+y＝12，
∴y＝﹣2x+12（3＜x＜6）；
（3）如图所示：
14．解：
（1）根据题意，填写下表如下：
故答案为：①200﹣x；②240﹣x；③60+x．
（2）A城运往C乡的肥料量为x吨，则运往D乡的肥料量为（200﹣x）吨；B城运往C、D乡的肥料量分别为（240﹣x）吨和（60+x）吨．
由总运费与各运输量的关系可知，
反映W与x之间的函数关系为W＝20x+25（200﹣x）+15（240﹣x）+24（60+x），
化简得W＝4x+10040（0≤x≤200）；
（3）由解析式可看出：当x＝0时，y有最小值10040．
因此，从A城运往C乡0吨，运往D乡200吨；从B城运往C乡240吨，运往D乡60吨，此时总运费最少，总运费最小值是10040元．
15．解：∵直线y1＝x+3与直线y2＝mx+交于点M（﹣1，2），
∴方程组的解是，
故答案为；
（2）由图象可得不等式x+3≤mx+的解集为：x≤﹣1，
故答案为x≤﹣1；
（3）∵直线y2＝mx+过点M（﹣1，2），
∴2＝﹣m+，解得m＝﹣，
∴直线BD的解析式为y＝﹣x+，
∴当y＝0时，x＝2，
∴B（2，0）．
∵直线AC的解析式为y＝x+3，
∴当y＝0时，x＝﹣3，
∴A（﹣3，0）．
∴AB＝5，
∴S△ABM＝×5×2＝5．
16．解：（1）∵直线l1：y＝﹣x+6分别与x轴、y轴交于点B、C，
∴当y＝0时，x＝12，
当x＝0时，y＝6，
∴B（12，0），C（0，6），
∵直线l1：y＝﹣x+6与直线l2：y＝x交于点A，
∴，
解得：，
∴A（6，3）；
故答案为：6，3；12，0；0，6；
（2）∵D是线段OA上，OA在直线l2：y＝x上，
∴设D（x，x），
∵△COD的面积为12，
∴×6×x＝12，
解得：x＝4，
∴D（4，2），
设直线CD的函数表达式是y＝kx+b，
把C（0，6），D（4，2）代入直线CD的函数表达式得：，
解得：，
∴直线CD的函数表达式为：y＝﹣x+6；
（3）∵以O、C、P、Q为顶点的四边形是菱形，
如图所示，分三种情况：
（i）当四边形OP1Q1C为菱形时，
∵∠COP1＝90°，
∴四边形OP1Q1C为正方形，
此时Q1P1＝OP1＝OC＝6，
∴Q1（6，6）；
（ii）当四边形OP2CQ2为菱形时，
∴CP2∥OQ2，P2Q2垂直平分OC，
∴直线OQ2由直线y＝﹣x+6向左平移6个单位得到，P2Q2∥x轴，
∴直线OQ2解析式为：y＝﹣x，
∵C坐标为（0，6），
∴Q2纵坐标为3，
把y＝3代入直线OQ2解析式y＝﹣x中，得：x＝﹣3，
∴Q2（﹣3，3）；
（iii）当四边形OQ3P3C为菱形时，
∴OQ3＝OC＝CP3＝P3Q3＝6，∠OCP3＝∠OQ3P3，
设Q3P3交x轴于点E，
∵直线CD的解析式为：y＝﹣x+6，
∴∠OCD＝45°，
∴∠OQ3P3＝45°，
∴△OEQ3是等腰直角三角形，
∴OE＝Q3E＝OQ3＝×6＝3，
∴Q3（3，﹣3），
综上所述，点Q的坐标是（6，6）或（﹣3，3）或（3，﹣3）．
17．（1）证明：对于直线y＝3x+6，
当x＝1﹣t时，y＝3（1﹣t）+6＝﹣3t+9，
∴P（1﹣t，9﹣3t）在直线y＝3x+6上．
（2）解：∵直线y＝3x+6分别与x轴、y轴交于B、C两点，
∴B（﹣2，0），C（0，6），
∵线段MN是由线段BC平移得到，
∴可以假设M（t，t﹣2），N（t+2，t﹣2+6），即N（t+2，t+4），
∵N（t+2，t+4）在直线y＝2x﹣4上，
∴t+4＝2（t+2）﹣4，
解得t＝4，
∴M（4，2），N（6，8），
∴BM＝＝2，BC＝＝2，
∴BM＝BC，
∵BC＝MN，BC∥MN，
∴四边形BMNC是平行四边形，
∵BC＝BM，
∴四边形BMNC是菱形．
（3）∵直线y＝mx﹣6m+8，
∴x＝6时，y＝8，
∴直线y＝mx﹣6m+8经过定点（6，8），
∴直线y＝mx﹣6m+8经过点N（6，8），
∵直线y＝mx﹣6m+8把四边形BMNC的面积分成1：3两部分，
∴直线y＝mx﹣6m+8经过BC的中点G或经过BM的中点H，
∵G是BC的中点，H是BM的中点，
∴G（﹣1，3），H（1，1），
把G（﹣1，3）代入y＝mx﹣6m+8得到m＝，
把H（1，1）代入y＝mx﹣6m+8得到m＝，
综上所述，满足条件的m的值为或．
18．解：（1）如图1中，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD＝2，∠ABC＝∠ADC＝60°，AC⊥BD，
∴△ABC，△ACD都是等边三角形，
∵∠AOB＝90°，∠ABO＝∠CBO＝30°，
∴OA＝AB＝1，OB＝OA＝，
∴AC＝2AO＝2，BD＝2OB＝2，
∴S菱形ABCD＝•BD•AC＝×2×2＝2．
（2）如图1中，过点A作AT⊥CD于T．
∵△ABC，△ACD都是等边三角形，
∴∠ACN＝∠ABM＝60°，AB＝AC，
∵∠MAN＝∠BAC＝60°，
∴∠BAM＝∠CAN，
∴△BAM≌△ACN（ASA），
∴BM＝CN＝4﹣2，
∵AC＝AD，AT⊥CD，
∴CT＝DT＝1，AT＝，
∴TN＝CT﹣CN＝1﹣（4﹣2）＝2﹣3，
∴AN＝＝＝3﹣，
∵S△ADN＝•AN•DG＝•DN•AT，
∴DG＝＝，
∴GN＝＝＝2﹣．
（3）如图2中，取CD的中点G，连接BG，CE，EG，过点G作GH⊥BD于H．
∵∠BAC＝∠PAE＝60°，
∴∠BAP＝∠CAE，
∵AB＝AC，AP＝AE，
∴△BAP≌△CAE（SAS），
∴∠ABP＝∠ACE＝30°，
∵∠ACD＝60°，
∴∠OCE＝∠GCE，
∵∠COD＝90°，∠ODC＝∠ADC＝30°，
∴CD＝2OC，
∵CG＝GD，
∴OC＝CG，
∵CE＝CE，
∴△OCE≌△GCE（SAS），
∴OE＝EG，
∴BE+OE＝BE+EG≥BG，
在Rt△BGH中，∵∠GHB＝90°，GH＝DG＝，BH＝，
∴BG＝＝＝，
∴BE+OE≥，
∴BE+OE的最小值为．
城、乡/吨数
A
B
C
x
①
D
②
③