2021届中考数学专题专练之函数（五）反比例函数B卷

这是一份2021届中考数学专题专练之函数（五）反比例函数B卷，共6页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1.已知反比例函数的图象经过点，那么这个反比例函数的解析式是( )
A.B.C.D.
2.如果反比例函数（m为常数）的图象经过点，那么m的取值范围是( )
A.B.C.D.
3.2019年10月，《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水，杜鹃花开”为设计理念，塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为土石方的任务，该运输公司平均运送土石方的速度v（单位：/天）与完成运送任务所需时间t（单位：天）之间的函数关系式是( )
A.B.C.D.
4.如图，函数和的图象将第一象限分成三个区域，点M是②区域内一点，轴于点N，则的面积可能是( )
A.0.5B.1C.2D.3.5
5.如图，点A，B是反比例函数图象上的两点，过点A，B分别作轴于点C，轴于点D，连接OA、BC，已知点，，，则等于( )
A.2B.3C.4D.6
6.若点在反比例函数的图象上，则的大小关系是( )
A.B.C.D.
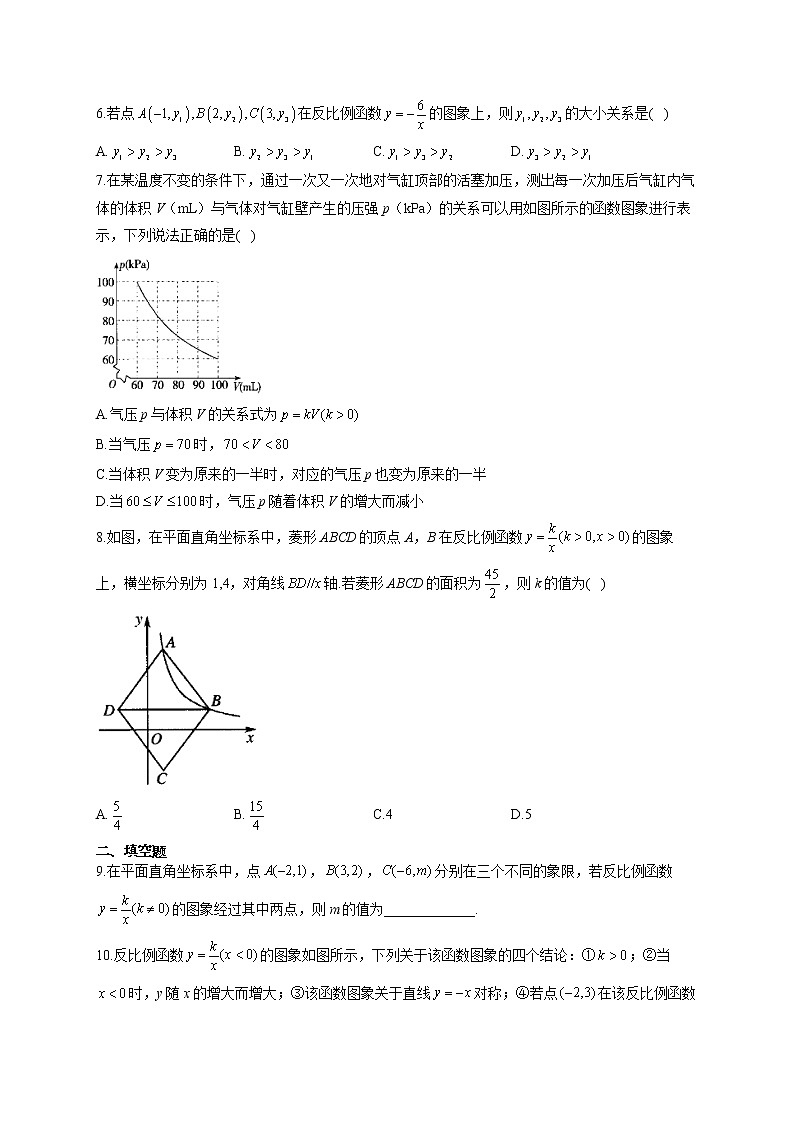
7.在某温度不变的条件下，通过一次又一次地对气缸顶部的活塞加压，测出每一次加压后气缸内气体的体积V（mL）与气体对气缸壁产生的压强p（kPa）的关系可以用如图所示的函数图象进行表示，下列说法正确的是( )
A.气压p与体积V的关系式为
B.当气压时，
C.当体积V变为原来的一半时，对应的气压p也变为原来的一半
D.当时，气压p随着体积V的增大而减小
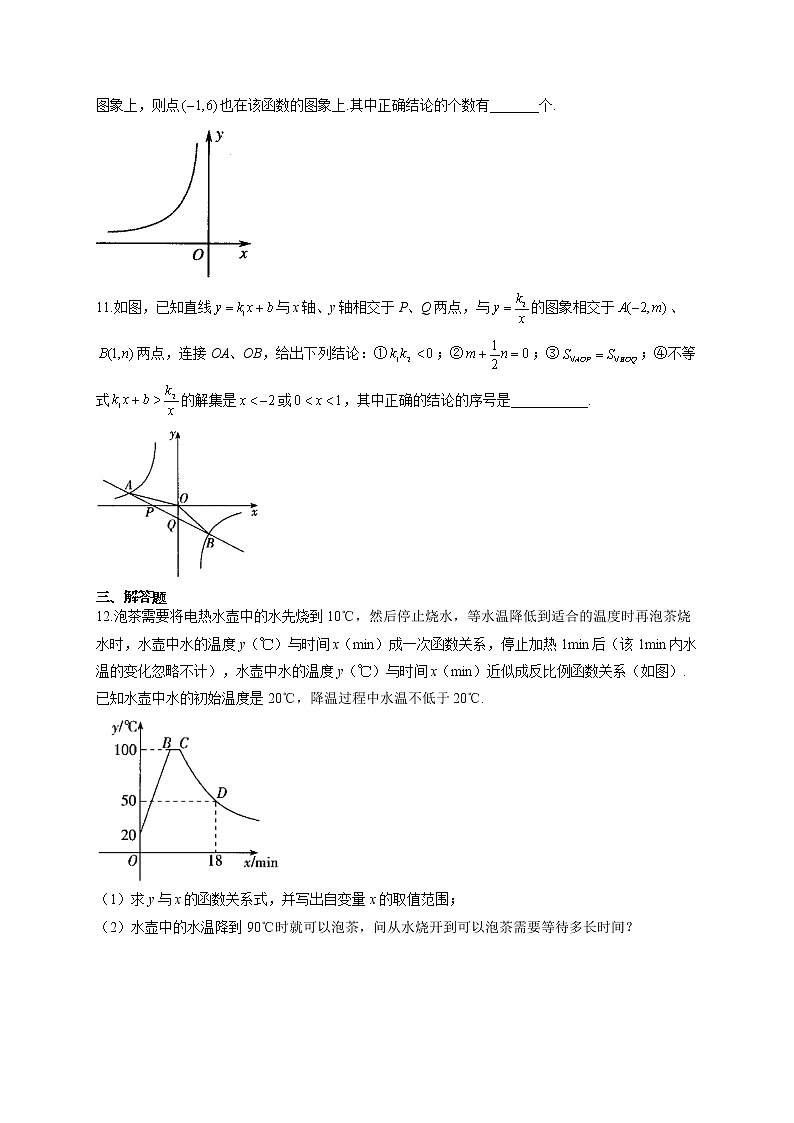
8.如图，在平面直角坐标系中，菱形ABCD的顶点A，B在反比例函数的图象上，横坐标分别为1,4，对角线轴.若菱形ABCD的面积为，则k的值为( )
A.B.C.4D.5
二、填空题
9.在平面直角坐标系中，点，，分别在三个不同的象限，若反比例函数的图象经过其中两点，则m的值为_____________.
10.反比例函数的图象如图所示，下列关于该函数图象的四个结论：①；②当时，y随x的增大而增大；③该函数图象关于直线对称；④若点在该反比例函数图象上，则点也在该函数的图象上.其中正确结论的个数有_______个.
11.如图，已知直线与x轴、y轴相交于P、Q两点，与的图象相交于、两点，连接OA、OB，给出下列结论：①；②；③；④不等式的解集是或，其中正确的结论的序号是___________.
三、解答题
12.泡茶需要将电热水壶中的水先烧到10℃，然后停止烧水，等水温降低到适合的温度时再泡茶烧水时，水壶中水的温度y（℃）与时间x（min）成一次函数关系，停止加热1min后（该1min内水温的变化忽略不计），水壶中水的温度y（℃）与时间x（min）近似成反比例函数关系（如图）.已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃.
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）水壶中的水温降到90℃时就可以泡茶，问从水烧开到可以泡茶需要等待多长时间？
参考答案
1.答案：D
解析：本题考查反比例函数的解析式.由题意可知点在反比例函数的图象上，设这个反比例函数的解析式为，则，解得，这个反比例函数的解析式为，故选D.
2.答案：D
解析：，，点A在第四象限，的图象的一支位于第四象限，，.
3.答案：A
解析：由题意，得，.故选A
4.答案：C
解析：点M是②区域内一点，轴于点N，，.故选C.
5.答案：D
解析：，轴，，，，，，，.点B是反比例函数图象上的点，.点A在该反比例函数的图象上，且轴，.故选D.
6.答案：C
解析：本题考查反比例函数的图象与性质.由题意可知反比例函数的图象在第二、四象限.点是函数图象在第二象限上的点，点和点是函数图象在第四象限上的点，是正数，和都是负数.又在每个象限中，随的增大而增大，，，即，故选C.
7.答案：D
解析：由物理知识知气压p与体积V成反比例关系，当时，，则，即，气压p与体积V的关系式为，故A不正确；当时，，故B不正确；当体积V变为原来的一半时，对应的气压p变为原来的2倍，故C不正确；当时，气压p随着体积V的增大而减小，故D正确.故选D.
8.答案：D
解析：本题考查菱形的性质、反比例函数的图象与性质、三角形的面积.如图，连接AC，交BD于点M，由菱形的性质可知，AC与BD互相垂直且平分，根据题意，设点A的坐标为，点B的坐标为，，，，，故选D.
9.答案：
解析：点，，分别在三个不同的象限，在第三象限，则反比例函数的图象经过B、C两点，即，.
10.答案：3
解析：本题考查反比例函数的图象与性质.根据反比例函数的图象可得；当时，y随x的增大而增大；该函数图象关于直线对称；若点在该反比例函数图象上可得，所以点也在该反比例函数图象上.综上所述，①错误，②③④正确，故正确结论的个数为3.
11.答案：②③④
解析：由题图知，，，，故①错误；把、代入中，得，，，，故②正确；把、代入得，，，，，，，又易知，，，，，，故③正确；由题图知不等式的解集是或，故④正确.
12.答案：（1）设反比例函数的解析式为，
当时，，，
解得，.
对于，当时，，
C点坐标为，
B点坐标为.
对于，当时，，
降温过程中y与x的函数关系式为.
设一次函数的解析式为，
点B的坐标为，
，
，
烧水时，y与x的函数关系式为.
停止加热1min内，y与x的函数关系式为.
y与x的函数关系式为.
（2）把代入，得,min.
因此从水烧开到可以泡茶需要等待2 min.