高三数学一轮复习： 第5章 第1节 数列的概念与简单表示法

这是一份高三数学一轮复习： 第5章 第1节 数列的概念与简单表示法，共8页。
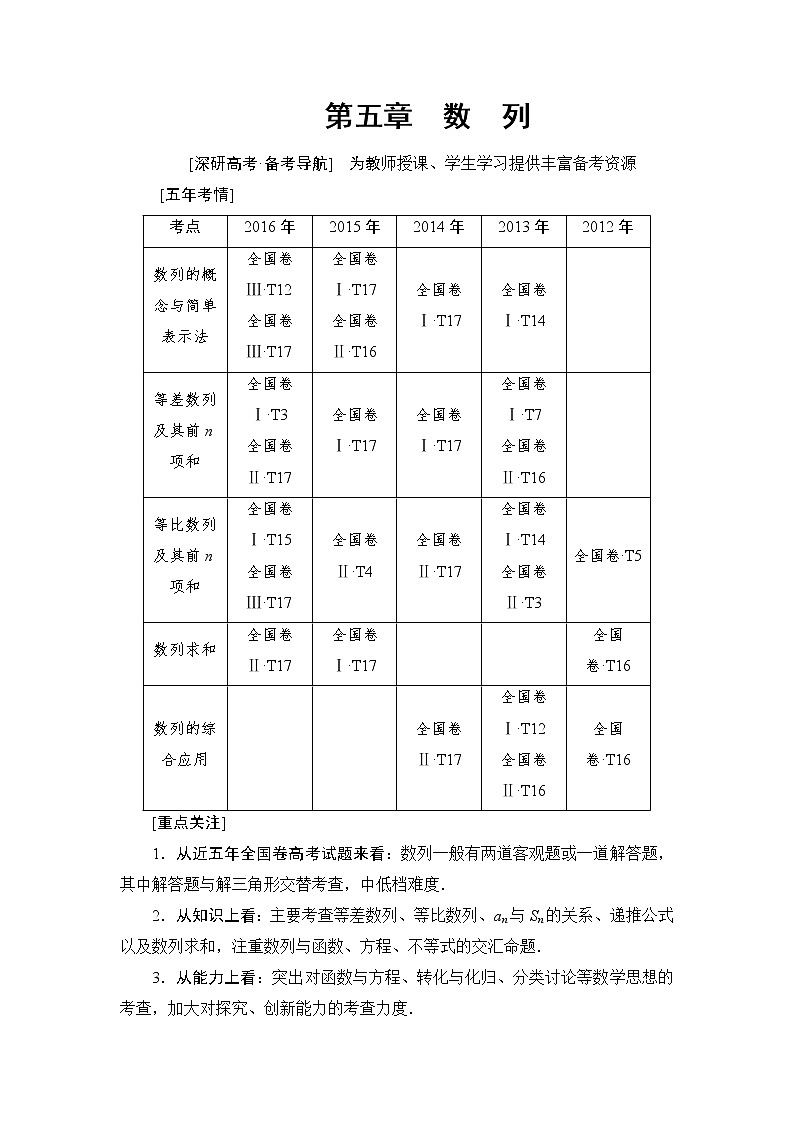
1．从近五年全国卷高考试题来看：数列一般有两道客观题或一道解答题，其中解答题与解三角形交替考查，中低档难度．
2．从知识上看：主要考查等差数列、等比数列、an与Sn的关系、递推公式以及数列求和，注重数列与函数、方程、不等式的交汇命题．
3．从能力上看：突出对函数与方程、转化与化归、分类讨论等数学思想的考查，加大对探究、创新能力的考查力度．
[导学心语]
1．重视等差、等比数列的复习，正确理解等差、等比数列的概念，掌握等差、等比数列的通项公式、前n项和公式，灵活运用公式进行等差、等比数列基本量的计算．
2．重视an与Sn关系、递推关系的理解与应用，加强由Sn求an，由递推关系求通项，由递推关系证明等差、等比数列的练习．
3．数列是特殊的函数，要善于用函数的性质，解决与数列有关的最值问题，等差(比)数列中共涉及五个量a1、an、Sn、d(q)、n，“知三求二”，体现了方程思想的应用．
一般数列求和，首先要考虑是否能转化为等差(比)数列求和，再考虑错位相减、倒序相加、裂项相消、分组法等求和方法．
重视发散思维、创新思维，有意识地培养创新能力．
第一节 数列的概念与简单表示法
[考纲传真] 1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).2.了解数列是自变量为正整数的一类特殊函数．
1．数列的定义
按照一定顺序排列着的一列数称为数列，数列中的每一个数叫做这个数列的项．
2．数列的分类
3.数列的表示法
数列有三种表示法，它们分别是列表法、图象法和解析法．
4．数列的通项公式
如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．
5．数列的递推公式
如果已知数列的第1项(或前几项)，且从第二项(或某一项)开始的任一项an与它的前一项an－1(或前几项)间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式．
6．an与Sn的关系
若数列{an}的前n项和为Sn，通项公式为an，
则an＝eq \b\lc\{\rc\ (\a\vs4\al\c1(S1，n＝1，,Sn－Sn－1，n≥2.))
1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)
(1)所有数列的第n项都能使用公式表达．( )
(2)根据数列的前几项归纳出数列的通项公式可能不止一个．( )
(3)如果数列{an}的前n项和为Sn，则对∀n∈N*，都有an＋1＝Sn＋1－Sn.( )
(4)若已知数列{an}的递推公式为an＋1＝eq \f(1,2an－1)，且a2＝1，则可以写出数列{an}的任何一项．( )
[答案] (1)× (2)√ (3)√ (4)√
2．设数列{an}的前n项和Sn＝n2，则a8的值为( )
A．15 B.16
C．49 D.64
A [当n＝8时，a8＝S8－S7＝82－72＝15.]
3．把1,3,6,10,15,21，…这些数叫做三角形数，这是因为以这些数目的点可以排成一个正三角形(如图5­1­1)．
图5­1­1
则第7个三角形数是( )
A．27 B.28
C.29 D.30
B [由题图可知，第7个三角形数是1＋2＋3＋4＋5＋6＋7＝28.]
4．(教材改编)数列1，eq \f(2,3)，eq \f(3,5)，eq \f(4,7)，eq \f(5,9)，…的一个通项公式an是__________．
eq \f(n,2n－1) [由已知得，数列可写成eq \f(1,1)，eq \f(2,3)，eq \f(3,5)，…，故通项为eq \f(n,2n－1).]
5．(2017·保定调研)在数列{an}中，已知a1＝1，an＋1＝2an＋1，则其通项公式an＝__________.
2n－1 [法一：由an＋1＝2an＋1，可求a2＝3，a3＝7，a4＝15，…，验证可知an＝2n－1.
法二：由题意知an＋1＋1＝2(an＋1)，∴数列{an＋1}是以2为首项，2为公比的等比数列，∴an＋1＝2n，∴an＝2n－1.]
写出下面各数列的一个通项公式：
(1)3,5,7,9，…；
(2)eq \f(1,2)，eq \f(3,4)，eq \f(7,8)，eq \f(15,16)，eq \f(31,32)，…；
(3)－1,7，－13,19，…；
(4)3,33,333,3 333，….
[解] (1)各项减去1后为正偶数，所以an＝2n＋1.3分
(2)每一项的分子比分母少1，而分母组成数列21,22,23,24，…，
所以an＝eq \f(2n－1,2n).6分
(3)数列中各项的符号可通过(－1)n表示，从第2项起，每一项的绝对值总比它的前一项的绝对值大6.
故通项公式为an＝(－1)n(6n－5).9分
(4)将数列各项改写为eq \f(9,3)，eq \f(99,3)，eq \f(999,3)，eq \f(9 999,3)，…，分母都是3，而分子分别是10－1,102－1,103－1,104－1，…，
所以an＝eq \f(1,3)(10n－1).12分
[规律方法] 1.求数列通项时，要抓住以下几个特征：
(1)分式中分子、分母的特征；
(2)相邻项的变化特征；
(3)拆项后变化的部分和不变的部分的特征；
(4)各项符号特征等，并对此进行归纳、化归、联想．
2．若关系不明显时，应将部分项作适当的变形，统一成相同的形式，让规律凸现出来．对于正负符号变化，可用(－1)n或(－1)n＋1来调整，可代入验证归纳的正确性．
[变式训练1] (1)数列0，eq \f(2,3)，eq \f(4,5)，eq \f(6,7)，…的一个通项公式为( )
A．an＝eq \f(n－1,n＋1)(n∈N*)B．an＝eq \f(n－1,2n＋1)(n∈N*)
C．an＝eq \f(2n－1,2n－1)(n∈N*)D．an＝eq \f(2n,2n＋1)(n∈N*)
(2)数列{an}的前4项是eq \f(3,2)，1，eq \f(7,10)，eq \f(9,17)，则这个数列的一个通项公式是an＝__________.
【导学号：01772171】
(1)C (2)eq \f(2n＋1,n2＋1) [(1)注意到分子0,2,4,6都是偶数，对照选项排除即可．
(2)数列{an}的前4项可变形为eq \f(2×1＋1,12＋1)，eq \f(2×2＋1,22＋1)，eq \f(2×3＋1,32＋1)，eq \f(2×4＋1,42＋1)，故an＝eq \f(2n＋1,n2＋1).]
已知下面数列{an}的前n项和Sn，求{an}的通项公式：
(1)Sn＝2n2－3n；
(2)Sn＝3n＋b.
[解] (1)a1＝S1＝2－3＝－1，
当n≥2时，an＝Sn－Sn－1＝(2n2－3n)－[2(n－1)2－3(n－1)]＝4n－5，3分
由于a1也适合此等式，∴an＝4n－5.5分
(2)a1＝S1＝3＋b，
当n≥2时，an＝Sn－Sn－1＝(3n＋b)－(3n－1＋b)＝2·3n－1.7分
当b＝－1时，a1适合此等式．
当b≠－1时，a1不适合此等式.10分
∴当b＝－1时，an＝2·3n－1；
当b≠－1时，an＝eq \b\lc\{\rc\ (\a\vs4\al\c1(3＋b，n＝1，,2·3n－1，n≥2.))12分
[规律方法] 由Sn求an的步骤
(1)先利用a1＝S1求出a1；
(2)用n－1替换Sn中的n得到一个新的关系，利用an＝Sn－Sn－1(n≥2)便可求出当n≥2时an的表达式；
(3)对n＝1时的结果进行检验，看是否符合n≥2时an的表达式，如果符合，则可以把数列的通项公式合写；如果不符合，则应写成分段函数的形式．
易错警示：利用an＝Sn－Sn－1求通项时，应注意n≥2这一前提条件，易忽视验证n＝1致误．
[变式训练2] (2017·石家庄质检(二))已知数列{an}的前n项和为Sn，若Sn＝2an－4(n∈N*)，则an＝( )
A．2n＋1 B.2n
C．2n－1 D.2n－2
A [由Sn＝2an－4可得Sn－1＝2an－1－4(n≥2)，两式相减可得an＝2an－2an－1(n≥2)，即an＝2an－1(n≥2)．又a1＝2a1－4，a1＝4，所以数列{an}是以4为首项，2为公比的等比数列，则an＝4×2n－1＝2n＋1，故选A.]
根据下列条件，确定数列{an}的通项公式：
(1)a1＝2，an＋1＝an＋3n＋2；
(2)a1＝1，an＋1＝2nan；
(3)a1＝1，an＋1＝3an＋2.
[解] (1)∵an＋1－an＝3n＋2，
∴an－an－1＝3n－1(n≥2)，
∴an＝(an－an－1)＋(an－1－an－2)＋…＋(a2－a1)＋a1
＝eq \f(n3n＋1,2)(n≥2)．
当n＝1时，a1＝eq \f(1,2)×(3×1＋1)＝2符合公式，
∴an＝eq \f(3,2)n2＋eq \f(n,2).4分
(2)∵an＋1＝2nan，∴eq \f(an,an－1)＝2n－1(n≥2)，
∴an＝eq \f(an,an－1)·eq \f(an－1,an－2)·…·eq \f(a2,a1)·a1
＝2n－1·2n－2·…·2·1＝21＋2＋3＋…＋(n－1)＝2eq \f(nn－1,2).
又a1＝1适合上式，故an＝2eq \f(nn－1,2).8分
(3)∵an＋1＝3an＋2，∴an＋1＋1＝3(an＋1)，
又a1＝1，∴a1＋1＝2，
故数列{an＋1}是首项为2，公比为3的等比数列，
∴an＋1＝2·3n－1，因此an＝2·3n－1－1.12分
[规律方法] 1.已知a1，且an－an－1＝f(n)，可用“累加法”求an；已知a1(a1≠0)，且eq \f(an,an－1)＝f(n)，可用“累乘法”求an.
2．已知a1，且an＋1＝qan＋b，则an＋1＋k＝q(an＋k)(其中k可由待定系数法确定)，可转化为{an＋k}为等比数列．
易错警示：本题(1)，(2)中常见的错误是忽视验证a1是否适合所求式，(3)中常见错误是忽视判定首项是否为零．
[变式训练3] (2016·全国卷Ⅲ)已知各项都为正数的数列{an}满足a1＝1，aeq \\al(2,n)－(2an＋1－1)an－2an＋1＝0.
(1)求a2，a3；
(2)求{an}的通项公式．
[解] (1)由题意可得a2＝eq \f(1,2)，a3＝eq \f(1,4).4分
(2)由aeq \\al(2,n)－(2an＋1－1)an－2an＋1＝0得
2an＋1(an＋1)＝an(an＋1).7分
因为{an}的各项都为正数，所以eq \f(an＋1,an)＝eq \f(1,2).9分
故{an}是首项为1，公比为eq \f(1,2)的等比数列，因此an＝eq \f(1,2n－1).12分
[思想与方法]
1．数列是一种特殊的函数，因此，在研究数列问题时，既要注意函数方法的普遍性，又要考虑数列方法的特殊性．
2．an＝eq \b\lc\{\rc\ (\a\vs4\al\c1(Snn＝1，,Sn－Sn－1n≥2.))
3．由递推关系求数列的通项的基本思想是转化，常用的方法是：
(1)an＋1－an＝f(n)型，采用叠加法．
(2)eq \f(an＋1,an)＝f(n)型，采用叠乘法．
(3)an＋1＝pan＋q(p≠0，p≠1)型，转化为等比数列解决．
[易错与防范]
1．数列是按一定“次序”排列的一列数，一个数列不仅与构成它的“数”有关，而且还与这些“数”的排列顺序有关．
2．易混项与项数是两个不同的概念，数列的项是指数列中某一确定的数，而项数是指数列的项对应的位置序号．
3．在利用数列的前n项和求通项时，往往容易忽略先求出a1，而是直接把数列的通项公式写成an＝Sn－Sn－1的形式，但它只适用于n≥2的情形．考点
2016年
2015年
2014年
2013年
2012年
数列的概念与简单表示法
全国卷Ⅲ·T12
全国卷Ⅲ·T17
全国卷Ⅰ·T17
全国卷Ⅱ·T16
全国卷Ⅰ·T17
全国卷Ⅰ·T14
等差数列及其前n项和
全国卷Ⅰ·T3
全国卷Ⅱ·T17
全国卷Ⅰ·T17
全国卷Ⅰ·T17
全国卷Ⅰ·T7
全国卷Ⅱ·T16
等比数列及其前n项和
全国卷Ⅰ·T15
全国卷Ⅲ·T17
全国卷Ⅱ·T4
全国卷Ⅱ·T17
全国卷Ⅰ·T14
全国卷Ⅱ·T3
全国卷·T5
数列求和
全国卷Ⅱ·T17
全国卷Ⅰ·T17
全国卷·T16
数列的综合应用
全国卷Ⅱ·T17
全国卷Ⅰ·T12
全国卷Ⅱ·T16
全国卷·T16
分类标准
类型
满足条件
项数
有穷数列
项数有限
无穷数列
项数无限
单调性
递增数列
an＋1>an
其中n∈N*
递减数列
an＋1