高考数学一轮复习 第9章 重点强化课5 统计与统计案例

这是一份高考数学一轮复习 第9章 重点强化课5 统计与统计案例，共16页。

重点强化课(五)　统计与统计案例
[复习导读]　本章是新课程改革增加内容，是命题的热点，以程序框图、回归分析、统计图表为重点，以客观题为主．命题注重背景新颖、角度灵活．但近几年统计与统计案例、统计与概率交汇，加大了考查力度.2015年、2016年全国卷均以解答题的形式呈现，强化统计思想方法和创新应用意识的考查，复习过程中应引起注意，多变换角度，注重新背景、新材料题目的训练．
重点1　程序框图及应用
角度1　程序框图与数列交汇
　执行如图1的程序框图，如果输入的N＝100，则输出的X＝(　　)
A．0.95　　　B．0.98　　　C．0.99　　　D．1.00

图1
C　[由程序框图知，输出的X表示数列的前99项和，
∴X＝＋＋…＋
＝＋＋…＋＝.]
角度2　程序框图与统计的渗透
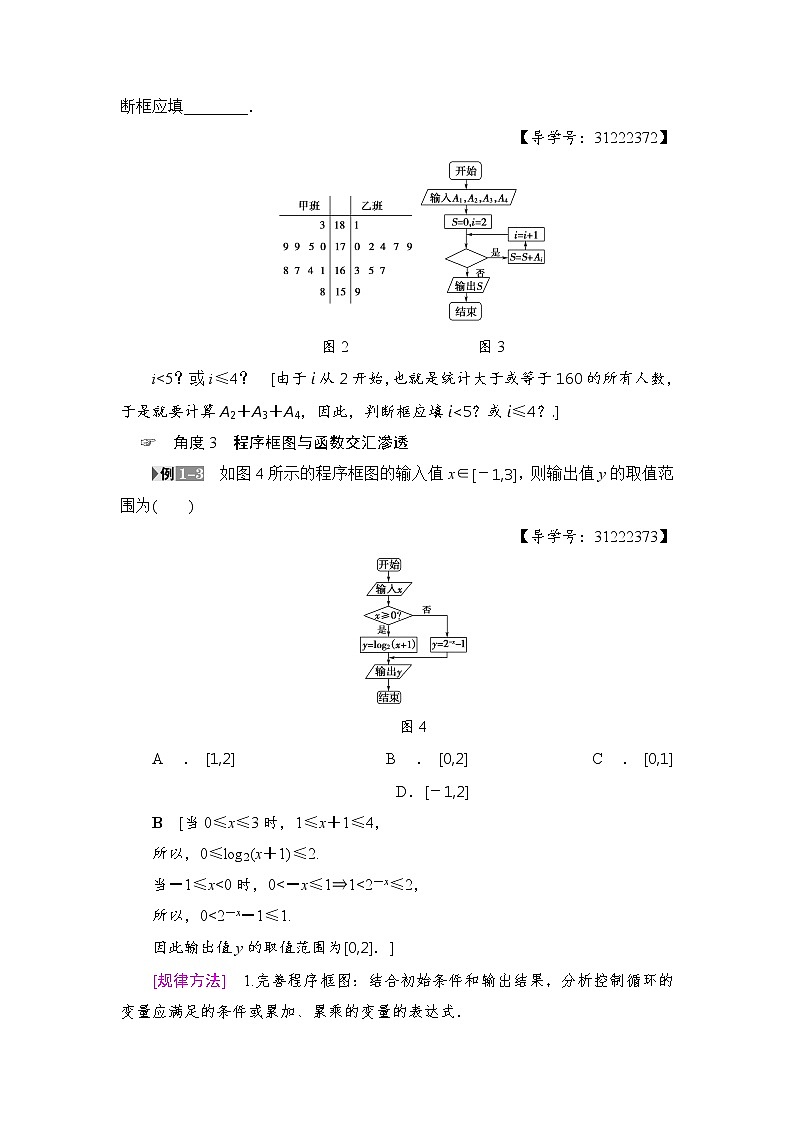
　(2017·合肥模拟)随机抽取某中学甲、乙两个班各10名同学，测量他们的身高获得身高数据的茎叶图如图2，在样本的20人中，记身高在[150,160)，[160,170)，[170,180)，[180,190)的人数依次为A1，A2，A3，A4.如图3是统计样本中身高在一定范围内的人数的算法框图．若图中输出的S＝18，则判断框应填________．
【导学号：31222372】

图2　　　　　　　　图3
i<5？或i≤4？　[由于i从2开始，也就是统计大于或等于160的所有人数，于是就要计算A2＋A3＋A4，因此，判断框应填i<5？或i≤4？.]
角度3　程序框图与函数交汇渗透
　如图4所示的程序框图的输入值x∈[－1,3]，则输出值y的取值范围为(　　)
【导学号：31222373】

图4
A．[1,2] B．[0,2] C．[0,1] D．[－1,2]
B　[当0≤x≤3时，1≤x＋1≤4，
所以，0≤log2(x＋1)≤2.
当－1≤x<0时，0<－x≤1⇒1<2－x≤2，
所以，0<2－x－1≤1.
因此输出值y的取值范围为[0,2]．]
[规律方法]　1.完善程序框图：结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．
2．求解该类问题，关键是准确理解程序框图的结构，明确程序框图的功能，按照程序框图中的条件进行程序．
重点2　用样本估计总体
　(2015·全国卷Ⅱ)某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表．
A地区用户满意度评分的频率分布直方图

①
图5
B地区用户满意度评分的频数分布表
满意度评分分组
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
2
8
14
10
6
(1)在图②中作出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值，给出结论即可)；
B地区用户满意度评分的频率分布直方图

②
图5
(2)根据用户满意度评分，将用户的满意度分为三个等级：
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
估计哪个地区用户的满意度等级为不满意的概率大？说明理由．
[解]　(1)如图所示．

通过两地区用户满意度评分的频率分布直方图可以看出，B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值；B地区用户满意度评分比较集中，而A地区用户满意度评分比较分散.5分
(2)A地区用户的满意度等级为不满意的概率大．
记CA表示事件：“A地区用户的满意度等级为不满意”；CB表示事件：“B地区用户的满意度等级为不满意”．由直方图得P(CA)的估计值为(0.01＋0.02＋0.03)×10＝0.6，P(CB)的估计值为(0.005＋0.02)×10＝0.25.
所以A地区用户的满意度等级为不满意的概率大.12分

[规律方法]　1.利用统计图表解决实际问题的关键在于从统计图表中提炼准确的数据信息．
2．本例通过画频率分布直方图考查对数据的处理能力和数形结合的思想方法，通过求概率考查运算求解能力和实际应用意识．
[对点训练1]　为调查甲、乙两校高三年级学生某次联考数学成绩情况，用简单随机抽样，从这两校中各抽取30名高三年级学生，以他们的数学成绩(百分制)作为样本，样本数据的茎叶图如图6所示.
　　　　甲　　　　

乙
　　　　　 7
4
5　　　　　
　　　5 3 3 2
5
3 3 8
　　　5 5 4 3 3 3 1 0 0
6
0 0 0 1 1 2 2 3 3 5
　　　　　 8 6 6 2 2 1 1 0 0
7
0 0 2 2 2 3 3 6 6 9
　　　　　 7 5 4 4 2
8
1 1 5 5 8
　　　　　 2 0
9
0　　　　　
图6
(1)若甲校高三年级每位学生被抽取的概率为0.05，求甲校高三年级学生总人数，并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格)；
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为1，2，估计1－2的值．
[解]　(1)设甲校高三年级学生总人数为n.
由题意知＝0.05，解得n＝600.2分
样本中甲校高三年级学生数学成绩不及格人数为5，据此估计甲校高三年级这次联考数学成绩的及格率为
×100%≈83%.5分
(2)设甲、乙两校样本平均数分别为′1，′2，
根据样本茎叶图可知30(′1－′2)＝30′1－30′2＝(7－5)＋(55＋8－14)＋(24－12－65)＋(26－24－79)＋(22－20)＋92＝2＋49－53－77＋2＋92＝15，
因此′1－′2＝0.5，
故1－2的估计值为0.5分.12分
重点3　统计的应用
　(2016·全国卷Ⅰ)某公司计划购买1台机器，该种机器使用三年后即被淘汰．机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

图7
记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用(单位：元)，n表示购机的同时购买的易损零件数．
(1)若n＝19，求y与x的函数解析式；
(2)若要求“需更换的易损零件数不大于n”的频率不小于0.5，求n的最小值；
(3)假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？
[解]　(1)当x≤19时，y＝3 800；
当x>19时，y＝3 800＋500(x－19)＝500x－5 700，
所以y与x的函数解析式为
y＝(x∈N).4分
(2)由柱状图知，需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7，故n的最小值为19.8分
(3)若每台机器在购机同时都购买19个易损零件，则这100台机器中有70台在购买易损零件上的费用为3 800，20台的费用为4 300,10台的费用为4 800，因此这100台机器在购买易损零件上所需费用的平均数为(3 800×70＋4 300×20＋4 800×10)＝4 000.10分
若每台机器在购机同时都购买20个易损零件，则这100台机器中有90台在购买易损零件上的费用为4 000，10台的费用为4 500，因此这100台机器在购买易损零件上所需费用的平均数为(4 000×90＋4 500×10)＝4 050.
比较两个平均数可知，购买1台机器的同时应购买19个易损零件.12分
[规律方法]　1.本题将分段函数、频率分布、样本的数字特征交汇命题，体现了统计思想的意识和应用．
2．本题易错点有两处：一是混淆频率分布直方图与柱状图致误；二是审题不清或不懂题意，导致解题无从入手．避免此类错误，需认真审题，读懂题意，并认真观察频率分布直方图与柱状图的区别，纵轴表示的意义．
[对点训练2]　某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关，随机抽取了55名市民，得到数据如下表：
喜欢
不喜欢
总计

大于40岁
20
5
25
20岁至40岁
10
20
30
总计
30
25
55
(1)判断是否在犯错误的概率不超过0.5%的前提下认为喜欢“人文景观”景点与年龄有关？
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率．
下面的临界值表供参考：
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式：K2＝，其中n＝a＋b＋c＋d)
[解]　(1)K2＝≈11.978>7.879，
所以在犯错误的概率不超过0.5%的前提下认为喜欢“人文景观”景点与年龄有关.5分
(2)设所抽样本中有m个“大于40岁”市民，则＝，得m＝4，所以样本中有4个“大于40岁”的市民，2个“20岁至40岁”的市民，分别记作B1，B2，B3，B4，C1，C2.
从中任选2人的基本事件有(B1，B2)，(B1，B3)，(B1，B4)，(B1，C1)，(B1，C2)，(B2，B3)，(B2，B4)，(B2，C1)，(B2，C2)，(B3，B4)，(B3，C1)，(B3，C2)，(B4，C1)，(B4，C2)，(C1，C2)，共15个.10分
其中恰有1名“大于40岁”和1名“20岁至40岁”的市民的事件有(B1，C1)，(B1，C2)，(B2，C1)，(B2，C2)，(B3，C1)，(B3，C2)，(B4，C1)，(B4，C2)，共8个．
所以恰有1名“大于40岁”的市民和1名“20岁至40岁”的市民的概率为P＝.12分
重点强化训练(五)　统计与统计案例
A组　基础达标
(建议用时：30分钟)
一、选择题
1．(2017·石家庄模拟)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43，则这四个社区驾驶员的总人数N为(　　)
A．101　　　　 B．808　　　　
C．1 212　　　　 D．2 012
B　[由题意知抽样比为，而四个社区一共抽取的驾驶员人数为12＋21＋25＋43＝101，故有＝，解得N＝808.]
2．设某大学的女生体重y(单位：kg)写身高x(单位：cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1,2，…，n)，用最小二乘法建立的回归方程为＝0.85x－85.71，则下列结论中不正确的是(　　)
A．y与x具有正的线性相关关系
B．回归直线过样本点的中心(，)
C．若该大学某女生身高增加1 cm，则其体重约增加0.85 kg
D．若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg
D　[∵0.85>0，∴y与x正相关，∴A正确；
∵回归直线经过样本点的中心(，)，∴B正确；
∵Δy＝0.85(x＋1)－85.71－(0.85x－85.71)＝0.85，
∴C正确．]
3．亚冠联赛前某参赛队准备在甲、乙两名球员中选一人参加比赛．如图8所示的茎叶图记录了一段时间内甲、乙两人训练过程中的成绩，若甲、乙两名球员的平均成绩分别是x1，x2，则下列结论正确的是(　　)

图8
A．x1>x2，选甲参加更合适
B．x1>x2，选乙参加更合适
C．x1＝x2，选甲参加更合适
D．x1＝x2，选乙参加更合适
A　[根据茎叶图可得甲、乙两人的平均成绩分别为x1≈31.67，x2≈24.17，从茎叶图来看，甲的成绩比较集中，而乙的成绩比较分散，因此甲发挥得更稳定，选甲参加比赛更合适．]
4．(2017·安徽皖南八校联考)某同学在研究性学习中，收集到某制药厂今年前5个月甲胶囊生产产量(单位：万盒)的数据如下表所示：
x(月份)
1
2
3
4
5
y(万盒)
5
5
6
6
8
若x，y线性相关，线性回归方程为＝0.7x＋，则估计该制药厂6月份生产甲胶囊产量为(　　)
A．8.1万盒 B．8.2万盒
C．8.9万盒 D．8.6万盒
A　[由题意知＝3，＝6，则＝－0.7＝3.9，∴x＝6时，＝8.1.]
5．(2017·郑州质量预测)利用如图9所示算法在平面直角坐标系上打印一系列点，则打印的点在圆x2＋y2＝10内的个数为(　　) 【导学号：31222374】

图9
A．2 B．3
C．4 D．5
B　[执行题中的程序框图，打印的点的坐标依次为(－3,6)，(－2,5)，(－1,4)，(0,3)，(1,2)，(2,1)，其中点(0,3)，(1,2)，(2,1)位于圆x2＋y2＝10内，因此打印的点位于圆x2＋y2＝10内的共有3个．]
二、填空题
6．在某市“创建文明城市”活动中，对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图10)，但是年龄组为[25,30)的数据不慎丢失，据此估计这800名志愿者年龄在[25,30)内的人数为________．
【导学号：31222375】

图10
160　[设年龄在[25,30)内的志愿者的频率是P，则有5×0.01＋P＋5×0.07＋5×0.06＋5×0.02＝1，解得P＝0.2.
故估计这800名志愿者年龄在[25,30)内的人数是800×0.2＝160.]
7．某新闻媒体为了了解观众对央视《开门大吉》节目的喜爱与性别是否有关系，随机调查了观看该节目的观众110名，得到如下的列联表：
女
男
总计

喜爱
40
20
60
不喜爱
20
30
50
总计
60
50
110
试根据样本估计总体的思想，估计约有________的把握认为“喜爱该节目与否和性别有关”．
参考附表：
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
99%　[假设喜爱该节目和性别无关，分析列联表中数据，可得K2＝≈7.822>6.635，
所以有99%的把握认为“喜爱《开门大吉》节目与否和性别有关”．]
8．(2017·太原模拟)数列{an}满足an＝n，阅读如图11所示的程序框图，运行相应的程序，若输入n＝5，an＝n，x＝2的值，则输出的结果v＝________.

图11
129　[该程序框图循环4次，各次v的值分别是14,31,64,129，故输出结果v＝129.]
三、解答题
9.(2017·桂林联考)如图12所示，茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况．乙组某个数据的个位数模糊，记为x，已知甲、乙两组的平均成绩相同．

图12
(1)求x的值，并判断哪组学生成绩更稳定；
(2)在甲、乙两组中各抽出一名同学，求这两名同学的得分之和低于20分的概率．
[解]　(1)甲＝＝10，
乙＝＝10，
∴x＝1，2分
又s＝[(10－9)2＋(10－9)2＋(11－10)2＋(11－10)2]＝1，
s＝[(10－8)2＋(10－9)2＋(11－10)2＋(12－10)2]＝，
∴s (2)记甲组4名同学为：A1，A2，A3，A4；乙组4名同学为：B1，B2，B3，B4.分别从甲、乙两组中各抽取一名同学所有可能的结果为：(A1，B1)，(A1，B2)，(A1，B3)，(A1，B4)，(A2，B1)，(A2，B2)，(A2，B3)，(A2，B4)，(A3，B1)，(A3，B2)，(A3，B3)，(A3，B4)，(A4，B1)，(A4，B2)，(A4，B3)，(A4，B4)，共16种.10分
其中得分之和低于20分的共6种，
∴得分之和低于20分的概率P＝＝.12分
10．(2015·重庆高考)随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款(年底余额)如下表：
年份
2010
2011
2012
2013
2014
时间代号t
1
2
3
4
5
储蓄存款y(千亿元)
5
6
7
8
10
(1)求y关于t的回归方程＝t＋；
(2)用所求回归方程预测该地区2015年(t＝6)的人民币储蓄存款．
附：回归方程＝t＋中，
＝，＝－ .
[解]　(1)列表计算如下：

这里n＝5，＝i＝＝3，＝i＝＝7.2.2分
又ltt＝－n 2＝55－5×32＝10，
lty＝iyi－n＝120－5×3×7.2＝12，
从而＝＝＝1.2，
＝－＝7.2－1.2×3＝3.6，
故所求回归方程为＝1.2t＋3.6.7分
(2)将t＝6代入回归方程可预测该地区2015年的人民币储蓄存款为＝1.2×6＋3.6＝10.8(千亿元).12分
B组　能力提升
(建议用时：15分钟)
1．如图13所示的程序框图，若输出k的值为6，则判断框内可填入的条件是(　　)

图13
A．s>？　　 B．s>？
C．s>？ D．s>？
C　[第一次执行循环：s＝1×＝，k＝8，s＝应满足条件；
第二次执行循环：s＝×＝，k＝7，s＝应满足条件，排除选项D；
第三次执行循环：s＝×＝，k＝6，不再满足条件，结束循环．
因此判断框中的条件为s>.]
2．(2017·西安调研)已知某产品连续4个月的广告费用x1(千元)与销售额y1(万元)，经过对这些数据的处理，得到如下数据信息：
①i＝18，i＝14；
②广告费用x和销售额y之间具有较强的线性相关关系；
③回归直线方程＝x＋中的＝0.8(用最小二乘法求得)．那么，广告费用为6千元时，可预测销售额约为________万元．
4．7　[因为i＝18，i＝14，所以＝4.5，＝3.5，
因为回归直线方程＝x＋中的＝0.8，
所以3.5＝0.8×4.5＋，
所以＝－0.1，所以＝0.8x－0.1.
x＝6时，可预测销售额约为4.7万元．]
3．(2015·广东高考)某工厂36名工人的年龄数据如下表.
　年龄
　年龄
　年龄
　年龄
1　　40
10　　36
19　　27
28　　34
2　　44
11　　31
20　　43
29　　39
3　　40
12　　38
21　　41
30　　43
4　　41
13　　39
22　　37
31　　38
5　　33
14　　43
23　　34
32　　42
6　　40
15　　45
24　　42
33　　53
7　　45
16　　39
25　　37
34　　37
8　　42
17　　38
26　　44
35　　49
9　　43
18　　36
27　　42
36　　39
(1)用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；
(2)计算(1)中样本的均值和方差s2；
(3)36名工人中年龄在－s与＋s之间有多少人？所占的百分比是多少(精确到0.01%)?
[解]　(1)36人分成9组，每组4人，其中第一组的工人年龄为44，所以它在组中的编号为2，
所以所有样本数据的编号为4n－2(n＝1,2，…，9)，
其年龄数据为：44,40,36,43,36,37,44,43,37.5分
(2)由均值公式知：＝＝40，
由方差公式知：s2＝[(44－40)2＋(40－40)2＋…＋(37－40)2]＝.8分
(3)因为s2＝，s＝，
所以36名工人中年龄在－s和＋s之间的人数等于年龄在区间[37,43]上的人数，
即40,40,41，…，39，共23人．
所以36名工人中年龄在－s和＋s之间的人数所占的百分比为×100%≈63.89%.12分