初中人教版21.2.1 配方法备课ppt课件

这是一份初中人教版21.2.1 配方法备课ppt课件，共18页。PPT课件主要包含了知识回顾，学习目标，课堂导入，整理得x225，知识点1，新知探究，例1解下列方程，12x28，跟踪训练，知识点2等内容，欢迎下载使用。

求出或表示出下列各数的平方根．121； (2) 0.81； (3) 0； (4) 3； (5) .
一个正数的平方根有两个，它们互为相反数，0的平方根为0，负数没有平方根.
1．掌握形如 x2=p(p≥0) 型方程的解法．2．掌握形如 (mx+n)2=p(m≠0，p≥0) 型方程的解法．
问题 一桶油漆可刷的面积为1500 dm2，李林用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面，你能算出盒子的棱长吗？
等量关系：10个正方体的表面积之和=1500
解:设盒子的棱长为x dm,则这个盒子的表面积为6x2 dm2， 根据一桶油漆可刷的面积,列出方程:
可以验证，5和-5是方程①的两个根，因为棱长不能是负值，所以盒子的棱长为5 dm．
10×6x2=1 500. ①
根据平方根的意义,得x=±5,即x1=5，x2=−5．
注意：用方程解决实际问题时，要考虑所得结果是否符合实际意义．
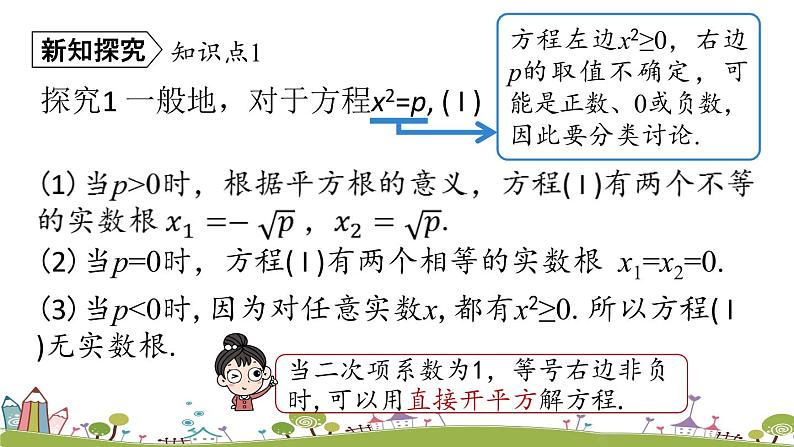
探究1 一般地，对于方程x2=p, ( I )
(2)当p=0时，方程( I )有两个相等的实数根 x1=x2=0.
(3)当p<0时,因为对任意实数x,都有x2≥0.所以方程( I )无实数根.
方程左边x2≥0，右边p的取值不确定，可能是正数、0或负数，因此要分类讨论.
当二次项系数为1，等号右边非负时,可以用直接开平方解方程.
（2）36x2-1=0．
解：二次项系数化为1，得 x2=4.
开平方，得 x=±2.
即x1=2，x2=-2.
解：移项,得36x2=1.
由方程(x + 3)2 = 5,可得
探究2 解方程：(x + 3)2 = 5.
解：由方程 x2 =25, 得 x =±5.由此想到：
于是,方程 (x + 3)2 = 5的两根为：
1.如何解形式为 (x+m)2=n (其中m，n 是常数)的一元二次方程呢？
（1）n<0,原方程无实根；
（2）n≥0,原方程的解为
2.如何解形式为 (mx+n)2=p (其中m≠0，p≥0)的一元二次方程呢？
(mx+n)2=p
直接开平方法适用于 x2=a (a≥0) 形式的一元二次方程的求解．这里的 x 既可以是字母，单项式，也可以是含有未知数的多项式．只要经过变形可以转化为 x2=a (a≥0) 形式的一元二次方程都可以用直接开平方法求解．
例2 解下列方程：
（1）(x+5)2=25；
(1)直接开平方，得 x+5=±5,
即x+5=5或x+5=-5.
所以x1=0, x2=-10.
（2）4(x-3)2-32=0．
移项，得4(x-3)2=32.
二次项系数化为1，得(x-3)2=8.
用直接开平方解一元二次方程方程的步骤
（1）2x2=8；（2）9x2-5=3；（3）(x+6)2-9=0；（4）3(x-1)2-6=0；（5）9x2+5=1．
用直接开平方法解方程 x2=a时，一定要确保a≥0，否则无实数根.
思考：如何解一元二次方程x2-4x+4=5.
整理，得(x-2)2=5.
当等号的左边不是一个完全平方形式时，我们要先把左边写成完全平方的形式，再用直接开平方解方程.
1．直接开平方法解一元二次方程的步骤：
2．两种数学思想：整体思想、转化思想．
1.用直接开平方法解下列一元二次方程，其中无实数根的方程为( ) A． x2+9=0B．-2x2=0 C．x2-3=0D．(x-2)2=0
选项A中，由 x2+9=0 得 x2=-9 ，故方程无实数根，故选A．
2.若关于 x 的方程 (x-2)2=a-5 有解，则 a 的取值范围为 ．
解：由题意可得 a-5≥0 ，所以 a≥5 ．
注意：当a≥0时,方程x2=a有解，当a<0时，方程无实数根.若方程中含有参数，则一定要分类讨论.