人教版九年级上册21.2.3 因式分解法背景图ppt课件

这是一份人教版九年级上册21.2.3 因式分解法背景图ppt课件，共20页。PPT课件主要包含了直接开平方法，配方法，公式法，因式分解法，知识回顾，学习目标，课堂导入，知识点，新知探究，跟踪训练等内容，欢迎下载使用。
解一元二次方程的方法：
会选择适当的方法（直接开平方法、配方法、公式法、因式分解法）解一元二次方程．
分别用配方法、公式法和因式分解法解方程 10x-4.9x2=0 .
解：10x-4.9x2=0化为一般式为4.9x2-10x=0.
∵ a=4.9，b=-10，c=0.
∴ b2-4ac= (-10)2-4×4.9×0=100.
解： 10x-4.9x2=0,x(10-4.9x) =0, x =0或10-4.9x=0,
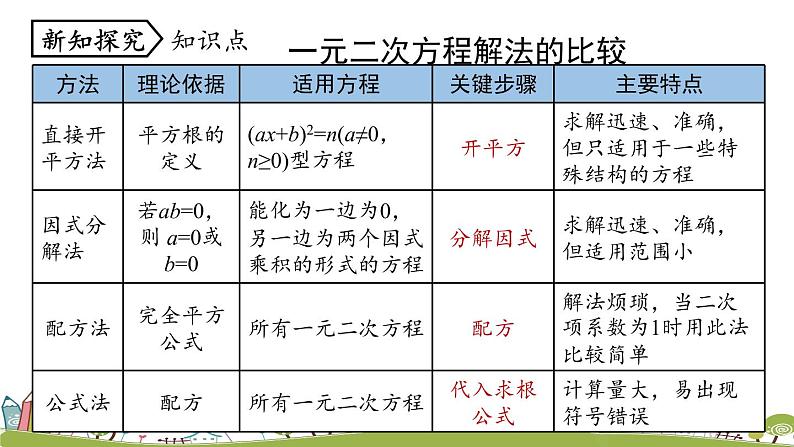
一元二次方程解法的比较
例 用适当的方法解方程：(1) 3x(x + 5)= 5(x + 5)；(2) (5x + 1)2=1；(3)x2 - 12x = 4； (4)3x2 = 4x + 1.
解：(1)化简，得 (3x-5)(x+5)=0.即3x-5=0 或 x+5=0.
(1)式左右两边可以提取公因式，所以用因式分解法解答较快.
(2) (5x + 1)2=1；
解： (2)开平方，得 5x + 1 = ±1.
方程一边以平方形式出现，另一边是常数，可用直接开平方法.
解： (3) 配方，得 x2-12x+62=4+62， 即 (x - 6)2 =40.
(3)x2 - 12x = 4;
二次项的系数为1，用配方法解题较快.
解： (4) 化为一般形式为 3x2 -4x-1=0. ∵Δ=b2 - 4ac = 28 > 0，
(4)3x2 = 4x + 1.
二次项的系数不为1，且不能直接开平方，也不能直接因式分解，所以适合公式法.
解一元二次方程的方法的选择技巧
若一元二次方程可化为 (mx+n)2=p(m≠0，p≥0) 的形式，则宜选用直接开平方法； 若一元二次方程的二次项系数为 1，一次项系数为偶数，则宜选用配方法； 若一元二次方程整理后右边为 0，且左边能进行因式分解，则宜选用因式分解法； 若直接开平方法、配方法、因式分解法都不简便，则宜选用公式法.
① x2-3x+1=0； ② 3x2-1=0； ③ -3t2+t=0； ④ x2-4x=2； ⑤ 2x2-x=0； ⑥ 5(m+2)2=8；⑦ 3y2-y-1=0； ⑧ 2x2+4x-1=0； ⑨ (x-2)2=2(x-2).适合运用直接开平方法 ；适合运用因式分解法 ；适合运用公式法 ；适合运用配方法 .
2.用适当的方法解下列方程：(1) x2-2x-8=0；(2) 2x2-7x+6=0；(3) (x-1)2-2x+2=0.
解：(1)移项，得 x2-2x=8，配方，得(x-1)2=9，所以x-1=±3，所以x1=4，x2=-2.
解：(2)因为 a=2，b=-7，c=6，所以 b2-4ac=1>0，
2.用适当的方法解下列方程：(2) 2x2-7x+6=0；
解:(3)原方程可化为 (x-1)2-2(x-1)=0，因式分解，得 (x-1)(x-1-2)=0，所以 x-1=0或 x-3=0，所以 x1=1，x2=3.
2.用适当的方法解下列方程：(3) (x-1)2-2x+2=0.
易错点：添括号，括号前是负号，各项要变号.
1.(2020·大兴安岭中考)解方程：x2﹣5x+6＝0
解：因式分解，得(x﹣2)(x﹣3)＝0，则x﹣2＝0或x﹣3＝0，解得x1＝2，x2＝3．
2.（2020•荆州中考）