2021年广东省广州市中考数学全真模拟试卷（2）

这是一份2021年广东省广州市中考数学全真模拟试卷（2），共27页。

2021年广东省广州市中考数学全真模拟试卷（2）
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）绝对值大于1而小于4的整数有（　　）个．
A．1 B．2 C．3 D．4
2．（3分）十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长到80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（　　）
A．8×1012 B．8×1013 C．8×1014 D．0.8×1013
3．（3分）下列运算正确的是（　　）
A．x2÷x﹣3＝x5 B．（a+2b）2＝a2+2ab+4b2
C．+＝ D．（x2y3）2＝x4y9
4．（3分）如图，数轴上点N表示的数可能是（　　）

A． B． C． D．
5．（3分）如图所示的几何体，从上面看得到的图形是（　　）

A． B． C． D．
6．（3分）如图，直线AD∥BC，若∠1＝40°，∠BAC＝80°，则∠2的度数为（　　）

A．40° B．50° C．60° D．70°
7．（3分）某校篮球队有12名队员，队员的年龄情况统计如下：
年龄/岁
13
14
15
16
人数
2
4
3
3
则这12名队员年龄的中位数和众数分别是（　　）
A．14，15 B．14.5，14 C．14，14 D．14.5，15
8．（3分）在下列方程中，有实数根的是（　　）
A．x2+3x+1＝0 B． C．x2+2x+3＝0 D．
9．（3分）若反比例函数的图象经过点（m，3m），且m≠0，则此反比例函数的图象在（　　）
A．第二、四象限 B．第一、二象限
C．第一、三象限 D．第三、四象限
10．（3分）如图，在△ABC中，∠CAB＝70°，∠B＝30°，在同一平面内，将△ABC绕点A逆时针旋转40°到△A′B′C′的位置，则∠CC′B′＝（　　）

A．10° B．15° C．20° D．30°
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）已知不等式组无解，那么a的取值范围是　 　．
12．（3分）如果一个正多边形的每个外角都等于72°，那么它是正　 　边形．
13．（3分）如图，AB是⊙O的直径，∠C＝14°，则∠BAD＝　 　度．

14．（3分）如图，矩形ABCD中，AB＝6，BC＝8，M是AD边上的一点，且AM＝2，点P在矩形ABCD所在的平面上，且∠BPD＝90°，则PM的最大值为　 　．

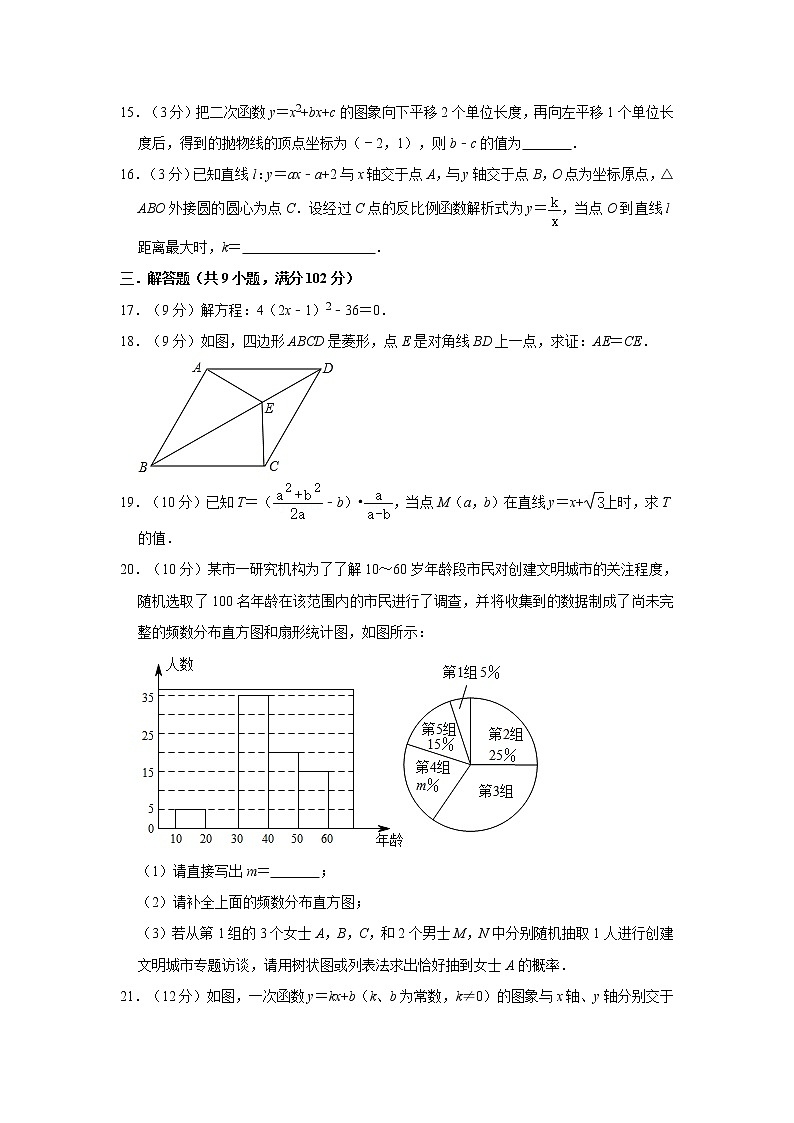
15．（3分）把二次函数y＝x2+bx+c的图象向下平移2个单位长度，再向左平移1个单位长度后，得到的抛物线的顶点坐标为（﹣2，1），则b﹣c的值为　 　．
16．（3分）已知直线l：y＝ax﹣a+2与x轴交于点A，与y轴交于点B，O点为坐标原点，△ABO外接圆的圆心为点C．设经过C点的反比例函数解析式为y＝，当点O到直线l距离最大时，k＝　 　．
三．解答题（共9小题，满分102分）
17．（9分）解方程：4（2x﹣1）2﹣36＝0．
18．（9分）如图，四边形ABCD是菱形，点E是对角线BD上一点，求证：AE＝CE．

19．（10分）已知T＝（﹣b）•，当点M（a，b）在直线y＝x+上时，求T的值．
20．（10分）某市一研究机构为了了解10～60岁年龄段市民对创建文明城市的关注程度，随机选取了100名年龄在该范围内的市民进行了调查，并将收集到的数据制成了尚未完整的频数分布直方图和扇形统计图，如图所示：

（1）请直接写出m＝　 　；
（2）请补全上面的频数分布直方图；
（3）若从第1组的3个女士A，B，C，和2个男士M，N中分别随机抽取1人进行创建文明城市专题访谈，请用树状图或列表法求出恰好抽到女士A的概率．
21．（12分）如图，一次函数y＝kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝（m为常数且m≠0）的图象在第二象限交于点C，CD⊥x轴，垂足为D，若OB＝2OA＝3OD＝6．
（1）求一次函数与反比例函数的解析式；
（2）求两个函数图象的另一个交点E的坐标；
（3）请观察图象，直接写出不等式kx+b≤的解集．

22．（12分）某零食店有甲，乙两种糖果，它们的单价分别为a元/千克，b元/千克．
（1）若购买甲5千克，乙2千克，共花费25元，购买甲3千克，乙4千克，共花费29元．
①求a和b的值；
②甲种糖果涨价m元/千克（0＜m＜2），乙种糖果单价不变，小明花了45元购买了两种糖果10千克，那么购买甲种糖果多少千克？（用含m的代数式表示）；
（2）小王购买了数量一样的甲、乙两种糖果，小李购买了总价一样的甲、乙两种糖果，请比较谁购买的平均价格更低．
23．（12分）如图，AB为半圆O的直径，且AB＝10，C为半圆上的一点，AC＜BC．
（1）请用尺规作图在BC上作一点D，使得BD＝AC+CD；（不写作法，保留痕迹）
（2）在（1）的条件下，连接OD，若OD＝，求△ABC的面积．

24．（14分）如图1，抛物线y＝ax2+bx+4（a＜0）与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C．
（1）求该抛物线对应的函数表达式，并写出其顶点M的坐标；
（2）试在y轴上找一点T，使得TM⊥TB，求T点的坐标；
（3）如图2，连接BC，点D是直线BC上方抛物线上的点，连接OD、CD，OD交BC于点F，当S△COF：S△CDF＝4：3时，求点D的坐标；
（4）如图3，点E的坐标为（0，﹣2），点P是抛物线上的动点，连接EB，PB，PE形成的△PBE中，是否存在点P，使得∠PBE或∠PEB等于2∠OBE？若存在，请直接写出符合条件的P点坐标；若不存在，请说明理由．
25．（14分）在△ABC中，∠ABC＝120°，线段AC绕点C顺时针旋转60°得到线段CD，连接BD．
（1）如图1，若AB＝BC，求证：BD平分∠ABC；
（2）如图2，若AB＝2BC，①求的值；
②连接AD，当S△ABC＝时，直接写出四边形ABCD的面积为　 　．


2021年广东省广州市中考数学全真模拟试卷（2）
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1．（3分）绝对值大于1而小于4的整数有（　　）个．
A．1 B．2 C．3 D．4
【分析】首先确定绝对值为2，3的数，从而可得答案．
【解答】解：绝对值大于1而小于4的整数有±2，±3，共4个．
故选：D．
2．（3分）十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长到80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（　　）
A．8×1012 B．8×1013 C．8×1014 D．0.8×1013
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：80万亿用科学记数法表示为8×1013．
故选：B．
3．（3分）下列运算正确的是（　　）
A．x2÷x﹣3＝x5 B．（a+2b）2＝a2+2ab+4b2
C．+＝ D．（x2y3）2＝x4y9
【分析】根据整式与二次根式的运算法则即可求出答案．
【解答】解：（B）原式＝a2+4ab+4b2，故B错误；
（C）由于与不是同类项二次根式，故C错误；
（D）原式＝x4y6，故D错误；
故选：A．
4．（3分）如图，数轴上点N表示的数可能是（　　）

A． B． C． D．
【分析】根据数轴可得点N表示的数大于3，小于4，再结合选项可得答案．
【解答】解：数轴上点N表示的数大于3，小于4，
因此可能是，
故选：C．
5．（3分）如图所示的几何体，从上面看得到的图形是（　　）

A． B． C． D．
【分析】根据从上边看得到的图形是俯视图，可得答案．
【解答】解：从上边看是一个六边形，中间为圆．
故选：D．
6．（3分）如图，直线AD∥BC，若∠1＝40°，∠BAC＝80°，则∠2的度数为（　　）

A．40° B．50° C．60° D．70°
【分析】根据平行线的性质，可以得到∠1+∠2+∠BAC＝180°，再根据题目中∠1＝40°，∠BAC＝80°，即可得到∠2的度数．
【解答】解：∵直线AD∥BC，
∴∠1+∠2+∠BAC＝180°，
∵∠1＝40°，∠BAC＝80°，
∴∠2＝60°，
故选：C．
7．（3分）某校篮球队有12名队员，队员的年龄情况统计如下：
年龄/岁
13
14
15
16
人数
2
4
3
3
则这12名队员年龄的中位数和众数分别是（　　）
A．14，15 B．14.5，14 C．14，14 D．14.5，15
【分析】众数就是出现次数最多的数，而中位数就是大小处于中间位置的数，根据定义即可求解．
【解答】解：这12名队员年龄的中位数＝14.5（岁），众数为14岁，
故选：B．
8．（3分）在下列方程中，有实数根的是（　　）
A．x2+3x+1＝0 B． C．x2+2x+3＝0 D．
【分析】一元二次方程要有实数根，则△≥0；算术平方根不能为负数；分式方程化简后求出的根要满足原方程．
【解答】解：A、△＝9﹣4＝5＞0，方程有实数根；
B、算术平方根不能为负数，故错误；
C、△＝4﹣12＝﹣8＜0，方程无实数根；
D、化简分式方程后，求得x＝1，检验后，为增根，故原分式方程无解．
故选：A．
9．（3分）若反比例函数的图象经过点（m，3m），且m≠0，则此反比例函数的图象在（　　）
A．第二、四象限 B．第一、二象限
C．第一、三象限 D．第三、四象限
【分析】根据反比例函数图象上点的坐标特征得到k＝m•3m＝3m2＞0，然后根据反比例函数的性质对各选项进行判断．
【解答】解：∵反比例函数的图象经过点（m，3m），且m≠0，
∴k＝m•3m＝3m2＞0，
∴此反比例函数的图象分布在第一、三象限．
故选：C．
10．（3分）如图，在△ABC中，∠CAB＝70°，∠B＝30°，在同一平面内，将△ABC绕点A逆时针旋转40°到△A′B′C′的位置，则∠CC′B′＝（　　）

A．10° B．15° C．20° D．30°
【分析】根据旋转的性质找到对应点、对应角进行解答．
【解答】解：∵在△ABC中，∠CAB＝70°，∠B＝30°，
∴∠ACB＝180°﹣70°﹣30°＝80°，
∵△ABC绕点A逆时针旋转40°得到△AB′C′，
∴∠CAC′＝40°，∠AC′B′＝∠ACB＝80°，AC＝AC′，
∴∠AC′C＝（180°﹣40°）＝70°，
∴∠CC′B′＝∠AC′B′﹣∠AC′C＝10°，
故选：A．
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）已知不等式组无解，那么a的取值范围是　a≥　．
【分析】先求出每个不等式的解集，再根据不等式组无解，结合口诀“大大小小无解了”可得关于m的不等式，解之可得答案．
【解答】解：解不等式x+7＞2x+a，得x＜7﹣a，
解不等式3x+8＞a，得：x＞，
∵不等式组无解，
∴≥7﹣a，
解得a≥，
故答案为：a≥．
12．（3分）如果一个正多边形的每个外角都等于72°，那么它是正　5　边形．
【分析】正多边形的外角和是360°，这个正多边形的每个外角相等，因而用360°除以外角的度数，就得到外角和中外角的个数，外角的个数就是多边形的边数．
【解答】解：这个正多边形的边数：360°÷72°＝5．
故答案为：5
13．（3分）如图，AB是⊙O的直径，∠C＝14°，则∠BAD＝　76　度．

【分析】连接BD，求出∠ADB和∠B即可得到答案．
【解答】解：连接BD，如图：

∵AB是⊙O的直径，
∴∠ADB＝90°，
∵∠C＝14°，
∴∠ABD＝14°，
∴∠BAD＝180°﹣∠ADB﹣∠ABD＝76°．
故答案为：76．
14．（3分）如图，矩形ABCD中，AB＝6，BC＝8，M是AD边上的一点，且AM＝2，点P在矩形ABCD所在的平面上，且∠BPD＝90°，则PM的最大值为　+5　．

【分析】如图，连接BD，以BD为直径作⊙O，则点P在⊙O上，作OE⊥AD于E，连接OM，PM，OP．
【解答】解：如图，连接BD，以BD为直径作⊙O，则点P在⊙O上，作OE⊥AD于E，连接OM，PM，OP．

∵OE⊥AD，
∴AE＝DE＝4，
∵OB＝OD，AE＝DE，
∴OE＝AB＝3，
∵AM＝2，
∴EM＝AE﹣AM＝2，
∴OM＝＝＝，
∵四边形ABCD是矩形，
∴∠BAD＝90°，BC＝AD＝8，
∴BD＝＝＝10，
∴OP＝OB＝OD＝5，
∵PM≤OM+OP，
∴PM≤+5，
∴PM的最大值为+5，
故答案为+5．
15．（3分）把二次函数y＝x2+bx+c的图象向下平移2个单位长度，再向左平移1个单位长度后，得到的抛物线的顶点坐标为（﹣2，1），则b﹣c的值为　﹣2　．
【分析】抛物线y＝x2+bx+c化为顶点坐标式再按照“左加右减，上加下减”的规律平移则可．
【解答】解：根据题意y＝x2+bx+c＝（x+）2+c﹣下平移2个单位，再向左平移1个单位，得y＝（x++1）2+c﹣﹣2．
∵抛物线的顶点坐标为（﹣2，1），
∴﹣﹣1＝﹣2，c﹣﹣2＝1，
解得：b＝2，c＝4，
∴b﹣c＝﹣2，
故答案为：﹣2．
16．（3分）已知直线l：y＝ax﹣a+2与x轴交于点A，与y轴交于点B，O点为坐标原点，△ABO外接圆的圆心为点C．设经过C点的反比例函数解析式为y＝，当点O到直线l距离最大时，k＝　　．
【分析】令x＝0，则y＝2﹣a，令y＝0则x＝，得到A（，0），B（0，2﹣a），由△ABO外接圆的圆心为点C得到点C是AB的中点，求得C（，），当点O到直线l距离最大时，△ABC是等腰直角三角形，根据等腰直角三角形的性质得到AO＝BO，于是得到结论．
【解答】解：∵直线l：y＝ax﹣a+2与x轴交于点A，与y轴交于点B，
令x＝0，则y＝2﹣a，令y＝0则x＝，
∴A（，0），B（0，2﹣a），
∵O点为坐标原点，
∴∠AOB＝90°，
∵△ABO外接圆的圆心为点C，
∴点C是AB的中点，
∴C（，），
∵直线y＝ax﹣a+2过定点D（1，2），
当点O到直线l距离最大时，AB⊥OD，

∵直线OD的解析式为y＝2x，
∴a＝﹣，
∴C（，）
∴k＝．
故答案为：．
三．解答题（共9小题，满分102分）
17．（9分）解方程：4（2x﹣1）2﹣36＝0．
【分析】根据直接开方法即可求出答案．
【解答】解：∵4（2x﹣1）2﹣36＝0，
∴（2x﹣1）2＝9，
∴2x﹣1＝±3，
∴x＝2或﹣1
18．（9分）如图，四边形ABCD是菱形，点E是对角线BD上一点，求证：AE＝CE．

【分析】根据菱形的性质可以得到BA＝BC，∠ABE＝∠CBE，然后即可证明∴△ABE≌△CBE，从而可以得到结论成立．
【解答】证明：∵四边形ABCD是菱形，
∴BA＝BC，∠ABE＝∠CBE，
在△ABE和△CBE中，
，
∴△ABE≌△CBE（SAS），
∴AE＝CE．
19．（10分）已知T＝（﹣b）•，当点M（a，b）在直线y＝x+上时，求T的值．
【分析】根据分式的减法和乘法可以化简题目中的式子，然后根据点M（a，b）在直线y＝x+上，可以得到a﹣b的值，然后代入化简后的式子，即可得到T的值．
【解答】解：T＝（﹣b）•
＝
＝
＝，
∵点M（a，b）在直线y＝x+上，
∴b＝a+，
∴a﹣b＝﹣，
当a﹣b＝﹣时，原式＝＝﹣，
即T的值是﹣．
20．（10分）某市一研究机构为了了解10～60岁年龄段市民对创建文明城市的关注程度，随机选取了100名年龄在该范围内的市民进行了调查，并将收集到的数据制成了尚未完整的频数分布直方图和扇形统计图，如图所示：

（1）请直接写出m＝　20　；
（2）请补全上面的频数分布直方图；
（3）若从第1组的3个女士A，B，C，和2个男士M，N中分别随机抽取1人进行创建文明城市专题访谈，请用树状图或列表法求出恰好抽到女士A的概率．
【分析】（1）由频数除以样本数目，求出所占百分比即可；
（2）求出第2组的人数，补全上面的频数分布直方图即可；
（3）画树状图，再由概率公式求解即可．
【解答】解：（1）20÷100＝20%，
∴m＝20，
故答案为：20；
（2）第2组的人数为：100×25%＝25（人），
补全频数分布直方图如图所示：

（3）画树状图如图：

共有6个等可能的结果，恰好抽到女士A的结果有2个，
∴恰好抽到女士A的概率为＝．
21．（12分）如图，一次函数y＝kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝（m为常数且m≠0）的图象在第二象限交于点C，CD⊥x轴，垂足为D，若OB＝2OA＝3OD＝6．
（1）求一次函数与反比例函数的解析式；
（2）求两个函数图象的另一个交点E的坐标；
（3）请观察图象，直接写出不等式kx+b≤的解集．

【分析】（1）先求出A、B、C坐标，再利用待定系数法确定函数解析式．
（2）两个函数的解析式作为方程组，解方程组即可解决问题．
（3）根据图象一次函数的图象在反比例函数图象的下方，即可解决问题．
【解答】解：（1）∵OB＝2OA＝3OD＝6，
∴OB＝6，OA＝3，OD＝2，
∵CD⊥OA，
∴DC∥OB，
∴＝，
∴＝，
∴CD＝10，
∴点C坐标是（﹣2，10），
∵B（0，6），A（3，0），
∴，解得，
∴一次函数为y＝﹣2x+6．
∵反比例函数y＝经过点C（﹣2，10），
∴m＝﹣20，
∴反比例函数解析式为y＝﹣．
（2）由解得或，
∴E的坐标为（5，﹣4）．
（3）由图象可知kx+b≤的解集是：﹣2≤x＜0或x≥5．

22．（12分）某零食店有甲，乙两种糖果，它们的单价分别为a元/千克，b元/千克．
（1）若购买甲5千克，乙2千克，共花费25元，购买甲3千克，乙4千克，共花费29元．
①求a和b的值；
②甲种糖果涨价m元/千克（0＜m＜2），乙种糖果单价不变，小明花了45元购买了两种糖果10千克，那么购买甲种糖果多少千克？（用含m的代数式表示）；
（2）小王购买了数量一样的甲、乙两种糖果，小李购买了总价一样的甲、乙两种糖果，请比较谁购买的平均价格更低．
【分析】（1）①根据等量关系：购买甲5千克，乙2千克，共花费25元；购买甲3千克，乙4千克，共花费29元；列出方程求解即可；
②可设购买甲种糖果x千克，则购买乙种糖果（10﹣x）千克，根据花了45元，列出方程即可求解；
（2）分别求出两个人购买的平均价格，再比较大小即可求解．
【解答】解：（1）①依题意有，
解得．
故a的值为3，b的值为5；
②设购买甲种糖果x千克，则购买乙种糖果（10﹣x）千克，依题意有
（3+m）x+5（10﹣x）＝45，
解得x＝．
故购买甲种糖果千克；
（2）小王购买的平均价格为元；
小李购买的平均价格为＝元；
∵﹣＝＝≥0，
∴如果a＝b则平均价格一样低 若a不等于b 则小李平均价格低．
23．（12分）如图，AB为半圆O的直径，且AB＝10，C为半圆上的一点，AC＜BC．
（1）请用尺规作图在BC上作一点D，使得BD＝AC+CD；（不写作法，保留痕迹）
（2）在（1）的条件下，连接OD，若OD＝，求△ABC的面积．

【分析】（1）延长BC，在BC的延长线上截取CE，使得CE＝AC，作线段BE的垂直平分线垂足为D，点D即为所求作．
（2）解直角三角形求出AC，BC，可得结论．
【解答】解：（1）如图，点D即为所求作．

（2）连接AE，OD．
∵OA＝OB，DE＝DB，
∴AE＝2OD＝6，
∵AB是直径，
∴∠ACE＝∠ACB＝90°，
在Rt△ACE中，AC＝EC，
∴AC＝AE＝6，
∴BC＝＝＝6，
∴S△ABC＝•AC•BC＝×6×8＝24．
24．（14分）如图1，抛物线y＝ax2+bx+4（a＜0）与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C．
（1）求该抛物线对应的函数表达式，并写出其顶点M的坐标；
（2）试在y轴上找一点T，使得TM⊥TB，求T点的坐标；
（3）如图2，连接BC，点D是直线BC上方抛物线上的点，连接OD、CD，OD交BC于点F，当S△COF：S△CDF＝4：3时，求点D的坐标；
（4）如图3，点E的坐标为（0，﹣2），点P是抛物线上的动点，连接EB，PB，PE形成的△PBE中，是否存在点P，使得∠PBE或∠PEB等于2∠OBE？若存在，请直接写出符合条件的P点坐标；若不存在，请说明理由．
【分析】（1）把点A（﹣1，0），B（4，0）代入y＝ax2+bx+4即可得解析式，从而可得顶点M坐标；
（2）设T为（0，b），直线TM解析式为y＝kx+b，直线TB解析式为y＝k′x+b′，根据TM⊥TB，k•k′＝﹣1列方程即可得答案；
（3）由S△COF：S△CDF＝4：3，设点F横坐标为4t，则点D横坐标为7t，可得直线OF解析式为，从而表示出D的坐标，代入y＝﹣x2+3x+4即可得答案；
（4）分四种情况：①作E（0，﹣2）关于x轴的对称轴E′（0，2），连接BE′并延长交抛物线于P1，则∠P1BE＝2∠OBE，②过E作EP2∥BP1交抛物线于P2，则∠P2EB＝∠P1BE＝2∠OBE，③作E′关于BE的对称点F，则∠FBE＝∠P1BE＝2∠OBE，直线BF与抛物线交点即为满足条件的P3，④作P2关于BE的对称点H，则∠HEB＝∠BEP2＝2∠OBE，直线EH与抛物线交点即为满足条件的P4，画出图形，分别求出P的坐标即可．
【解答】解：（1）把点A（﹣1，0），B（4，0）代入y＝ax2+bx+4得：
解得，
∴y＝﹣x2+3x+4＝﹣（x﹣）2+，
∴顶点M（，）；
（2）设T为（0，t），
∵M（，），B（4，0），
设直线TM解析式为y＝kx+b，将M（，），T（0，t）代入得，
解得k＝，
设直线TB解析式为y＝k′x+b′，将B（4，0），T（0，t）代入得，
解得k′＝﹣，
∵TM⊥TB，
∴k•k′＝﹣1，即•（﹣）＝﹣1，
∴4t2﹣25t+24＝0，
解得：t1＝，t2＝，
∴T（0，）或T（0，）；
（3）在y＝﹣x2+3x+4中令x＝0得y＝4，
∴C（0，4），
而B（4，0），
∴BC解析式为y＝﹣x+4，
令点D、F的横坐标分别为xD，xF，
∵S△COF：S△CDF＝4：3，
∴，即，
∴，
设点F横坐标为4t，则点D横坐标为7t，
∵点F在直线BC上，则y＝﹣4t+4，
∴F（4t，4﹣4t），
设直线OF解析式为y＝mx，则4﹣4t＝4tm，
∴m＝
∴直线OF解析式为，
∵点D在直线OF上，则y＝•7t＝7﹣7t，
∴D（7t，7﹣7t），
将D（7t，7﹣7t）代入y＝﹣x2+3x+4中，得：7﹣7t＝﹣（7t）2+3×7t+4，
解得：，，
∴D的坐标为：（1，6）或（3，4）；
（4）分四种情况：
①作E（0，﹣2）关于x轴的对称轴E′（0，2），连接BE′并延长交抛物线于P1，则∠P1BE＝2∠OBE，如图：

∵E′（0，2），B（4，0），
∴E′B解析式为y＝﹣x+2，
由得（与B重合，舍去）或，
∴P1（﹣，）；
②过E作EP2∥BP1交抛物线于P2，则∠P2EB＝∠P1BE＝2∠OBE，如图：

∵E′B解析式为y＝﹣x+2，E（0，﹣2）
∴EP2解析式为y＝﹣x﹣2，
由得或（第三象限，此时∠P2EB≠∠P1BE不符合题意，舍去），
∴P2（，﹣），
③作E′关于BE的对称点F，直线BF与抛物线交点即为满足条件的P3，∠FBE＝∠P1BE＝2∠OBE，如图：

由E（0，﹣2），B（4，0）得EB解析式为y＝x﹣2，
E′F⊥BE且E′（0，2）可得E′F解析式为：y＝﹣2x+2，
由得G（，﹣），
设F（n，﹣2n+2），
∵E′G＝FG，
∴（0﹣）2+（﹣﹣2）2＝（n﹣）2+（﹣+2n﹣2）2，解得n＝0（舍去）或n＝，
∴F（，﹣），
而B（4，0），
∴直线BF解析式是y＝x﹣22，
由得（舍去）或，
∴P3（﹣，﹣），
④作P2关于BE的对称点H，直线EH与抛物线交点即为满足条件的P4，∠HEB＝∠BEP4＝2∠OBE，如图：

方法同③，可得P4（，），
综上所述，∠PBE或∠PEB等于2∠OBE，则P的坐标为：（﹣，）或（，﹣）或（﹣，﹣）或（，）．
25．（14分）在△ABC中，∠ABC＝120°，线段AC绕点C顺时针旋转60°得到线段CD，连接BD．
（1）如图1，若AB＝BC，求证：BD平分∠ABC；
（2）如图2，若AB＝2BC，①求的值；
②连接AD，当S△ABC＝时，直接写出四边形ABCD的面积为　　．

【分析】（1）连接AD，证△ACD是等边三角形，再证△ABD≌△CBD，推出∠CBD＝∠ABD，即得出结论；
（2）①连接AD，作等边三角形ACD的外接圆⊙O，证点B在⊙O上，在BD上截取BM，使BM＝BC，证△CBA≌△CMD，设BC＝BM＝1，则AB＝MD＝2，BD＝3，过点C作CN⊥BD于N，可求出BN＝BC＝，CN＝BC＝，ND＝BD﹣BN＝，CD＝，即可求出＝＝；
②分别过点B，D作AC的垂线，垂足分别为H，Q，设CB＝1，AB＝2，CH＝x，则由①知，AC＝，AH＝﹣x，在Rt△BCH与Rt△BAH中利用勾股定理求出BH的值，再求出DQ的值，求出＝，因为AC为△ABC与△ACD的公共底，所以＝，可求出△ACD的面积，进一步求出四边形ABCD的面积．
【解答】（1）证明：连接AD，
由题意知，∠ACD＝60°，CA＝CD，
∴△ACD是等边三角形，
∴CD＝AD，
又∵AB＝CB，BD＝BD，
∴△ABD≌△CBD（SSS），
∴∠CBD＝∠ABD，
∴BD平分∠ABC；

（2）解：①连接AD，作等边三角形ACD的外接圆⊙O，
∵∠ADC＝60°，∠ABC＝120°，
∴∠ADC+∠ABC＝180°，
∴点B在⊙O上，
∵AD＝CD，
∴，
∴∠CBD＝∠CAD＝60°，
在BD上截取BM，使BM＝BC，
则△BCM为等边三角形，
∴∠CMB＝60°，
∴∠CMD＝120°＝∠CBA，
又∵CB＝CM，∠BAC＝∠BDC，
∴△CBA≌△CMD（AAS），
∴MD＝AB，
设BC＝BM＝1，则AB＝MD＝2，
∴BD＝3，
过点C作CN⊥BD于N，
在Rt△BCN中，∠CBN＝60°，
∴∠BCN＝30°，
∴BN＝BC＝，CN＝BC＝，
∴ND＝BD﹣BN＝，
在Rt△CND中，
CD＝＝＝，
∴AC＝，
∴＝＝；

②如图3，分别过点B，D作AC的垂线，垂足分别为H，Q，
设CB＝1，AB＝2，CH＝x，
则由①知，AC＝，AH＝﹣x，
在Rt△BCH与Rt△BAH中，
BC2﹣CH2＝AB2﹣AH2，
即1﹣x2＝22﹣（﹣x）2，
解得，x＝，
∴BH＝＝，
在Rt△ADQ中，DQ＝AD＝×＝，
∴＝＝，
∵AC为△ABC与△ACD的公共底，
∴＝＝，
∵S△ABC＝，
∴S△ACD＝，
∴S四边形ABCD＝+＝，
故答案为：．