初中数学人教版九年级下册28.2 解直角三角形及其应用课文内容ppt课件

这是一份初中数学人教版九年级下册28.2 解直角三角形及其应用课文内容ppt课件，共49页。PPT课件主要包含了知识点1，PB之间的距离，知识点2，基础巩固，综合应用，方向角，复习巩固，∴AD⊥BC，解由题意可得，综合运用等内容，欢迎下载使用。

　　前面我们学习了仰角和俯角，那么你们知道方位角的概念吗？
　　从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角。
　　今天我们要学习的内容就与方位角有关.
学习目标： 1.能根据方向角画出相应的图形，会用解直 角三角形的知识解决方位问题. 2.知道坡度与坡角的含义，能利用解直角三 角形的知识解决与坡度有关的实际问题.
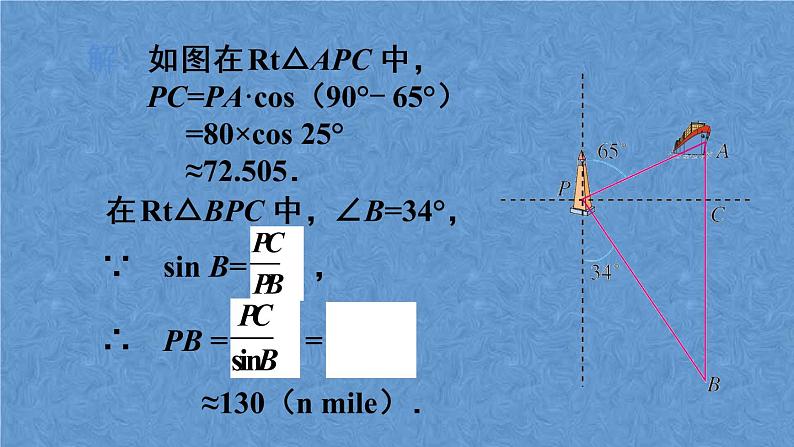
例1 一艘海轮位于灯塔 P 的北偏东 65°方向，距离灯塔 80 n mile 的 A 处，它沿正南方向航行一段时间后，到达位于灯塔 P 的南偏东 34°方向上的 B 处，这时， B 处距离灯塔 P 有多远（结果取整数）？
方向角类型的解直角三角形问题
思考：根据题意，你能画出示意图吗？
结合题目的条件，你能确定图中哪些线段和角？
PA= 80，∠A= 65° ，∠B= 34° .
要求的问题是什么？你能写出解答过程吗？
解：如图在 Rt△APC 中，　　PC=PA·cs（90°- 65°）　　　 =80×cs 25°　　　 ≈72.505．
　　a.将实际问题抽象为数学问题；b.根据问题中的条件，适当选用锐角三角函数解直角三角形；c.得到数学问题的答案；d.得到实际问题的答案.
　　你能小结出利用解直角三角形的知识解决实际问题的一般思路吗？
1.海中有一个小岛A，它周围8n mile内有暗礁.渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12n mile到达D点，这时测得小岛A在北偏东30°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？
解：过A点作AE⊥BD于E点.
易证∠A=∠ABD=30°，∴AD=BD=12 n mile.
∴AE=AD·sin60°
坡度类型的解直角三角形问题
问题：我们经常说某某山的坡度很陡，那么坡度究竟是指什么呢？
你能根据图示给出坡度的定义吗？
2.如图，拦水坝的横断面为梯形 ABCD，AF=DE=6m，斜面坡度 i =1:1.5 是指坡面的铅直高度 AF 与水平宽度 BF 的比，斜面坡度 i =1:3 是指DE 与CE 的比，根据图中数据，求： （1）坡角α 和 β 的度数；（2）斜坡 AB 的长(结果保留小数点后一位)．
解 ：（1）∵tanα＝1:1.5，tanβ＝1:3， 利用计算器可求得α≈33.7°，β≈18.4°；（2）∵tanα＝1:1.5，又AF＝6m， ∴BF＝9m，由勾股定理得 AB≈10.8m.
1. 已知外婆家在小明家的正东方，学校在外婆家的北偏西40°，外婆家到学校与小明家到学校的距离相等，则学校在小明家的（ ）A.南偏东50°B.南偏东40°C.北偏东50°D.北偏东40°
2.如图，某村准备在坡度为i=1:1.5的斜坡上栽树，要求相邻两棵树之间的水平距离为5 m，则这两棵树在坡面上的距离AB为 m.（结果保留根号）
3.为方便行人横过马路，打算修建一座高5 m的过街天桥.已知天桥的斜面坡度为1:1.5，计算斜坡AB的长度(结果取整数).
4.某型号飞机的机翼形状如图所示.根据图中数据计算AC,BD和AB的长度(结果保留小数点后两位).
解：如图所示，在Rt△BDE中，BE=5.00，∠DBE=30°,
在Rt△ACF中，CF=BE=5.00，∠FCA=45°，
　　从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角.
解：如图，∠PAB=30°，AP=32.∴PB= AP=16（n mile）.
∴PB＜16 n mile，轮船有触礁危险.
又∵AP=32，PC=16 ，∴∠PAC=45°,∴α =15°.
假设轮船沿东偏南α恰好能安全通过，此时航线AC与⊙P相切，即PC⊥AC.
∴轮船自A处开始至少沿南偏东75°方向航行,才能安全通过这一海域.
1.从课后习题中选取；2.完成练习册本课时的习题。
2. 如图，厂房屋顶人字架（等腰三角形）的跨度BC=10m，∠B＝36°，求中柱AD（D为底边中点）和上弦AB的长？（结果保留小数点后两位）
解：∵AB=AC，D为BC的中点，
∴AD=5×tan36°≈ 3.6 (m).
3. 如图，某飞机于空中A处探测到目标C，此时飞行高度AC＝1200m，从飞机上看地平面指挥台B的俯角α＝16°31′。求飞机A到指挥台B的距离？（结果保留整数）
解：由题意可知，在Rt△ABC中，
因此飞机A到指挥台B的距离约为4221m.
4. 从高出海平面55m的灯塔处收到一艘帆船的求助信号，从灯塔看帆船的俯角为21°，帆船距灯塔有多远？（结果保留整数）
解：如图所示，由题意可得∠B=21°，AC=55m.
因此帆船距灯塔约143m.
5.如图，在山坡上种树，要求株距（相邻两树间的水平距离）是5.5m，测得斜坡的倾斜角为24度，求斜坡上相邻两树间的坡面距离。
答：斜坡上相邻两树间的距离约为6.0m.
6.在Rt△ABC中，∠C=90°.（1）已知∠A，c，写出解Rt△ABC的过程；（2）已知∠A，a ，写出解Rt△ABC的过程；（3）已知a，c，写出解Rt△ABC的过程；
(1)∠B=180°-90°-∠A=90°-∠A， a=c·sinA，b=c·csA；
由sinA = ，求出∠A，∠B=90°－∠A.
7.如图，一座金字塔被发现时，顶部已荡然无存，但底部未曾受损.已知金字塔的下底面是一个边长为130m的正方形，且每一个侧面与底面成65°角，这座金字塔原来有多高（结果取整数？）
解：设这座金字塔原来高x m， 由题意得
∴x=65×tan65°≈139.
答：这座金字塔原来高约139m.
8.如图，一枚运载火箭从地面L处发射.当火箭到达A点时，从位于地面R处的雷达站测得AR的距离是6km，仰角为43°；1 s后火箭到达B点，此时测得仰角为45.54°，这枚火箭从A到B的平均速度是多少（结果取小数点后两位）？
解：在Rt△ALR中，AL=AR·sin∠ARL=6×sin43°≈ 4.092 (km),
LR=AR·cs∠ARL=6×cs43°≈ 4.388 (km).
在Rt△BRL中，BL=RL·tan∠BRL≈4.388×tan45.54°≈4.472 (km)，
9.为方便行人横过马路，打算修建一座高5 m的过街天桥.已知天桥的斜面坡度为1:1.5，计算斜坡AB的长度(结果取整数).
11.根据图中标出的百慕大三角的位置，计算百慕大三角的面积（结果取整数）.
解：如图，过B作直线分别垂直AD于D，CE于E，在Rt△ABD中，∠BAD=62°，AB=1700km.
∴BD=AB·sin∠BAD=1700×sin62°，
AD=AB·cs∠BAD=1700×cs62°.
在Rt△BCE中，∠BCE=54°，BC=2720km,
∴BE=BC·sin∠BCE=2720×sin54°.
CE=BC·cs∠BCE=2720×cs54°.
S△ABC=S梯形ADEC-S△ABD-S△BCE