初中人教版27.3 位似教案配套课件ppt

这是一份初中人教版27.3 位似教案配套课件ppt，共27页。PPT课件主要包含了学习目标，新课导入，直角坐标系中的变换，知识点1，知识讲解，kxky，位似图形的坐标规律，即学即练，随堂练习，相似比为2∶1等内容，欢迎下载使用。
1.进一步熟悉位似的作图.2.会用坐标的变化来表示图形的位似变换.3.会根据位似图形上的点的坐标变化的规律，在坐标系中画一个图形以原点为位似中心的位似图形.
首先确定位似中心，位似中心的位置可随意选择（除非题目指明）； 确定原图形的关键点，如四边形有四个关键点，即它的四个顶点； 确定位似比，根据位似比的取值，可以判断是将一个图形放大还是缩小； 符合要求的图形不惟一，因为所作图形与所确定的位似中心的位置有关，并且同一个位似中心的两侧各有一个符合要求的图形，最好做两个.
作位似图形有哪些步骤？
位似图形在直角坐标系中又有什么规律呢？
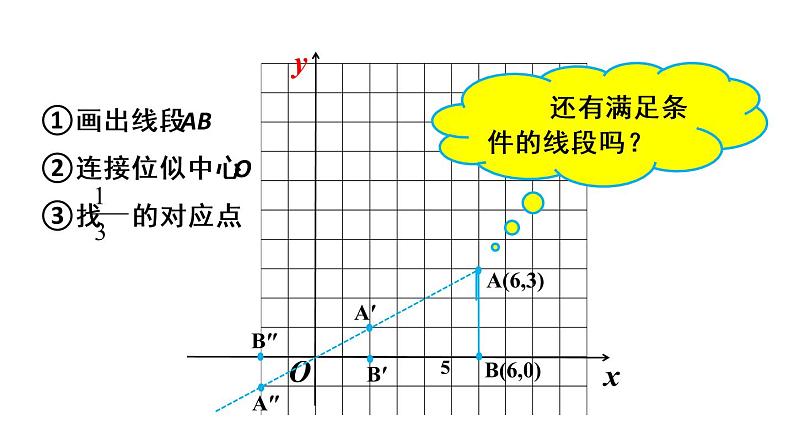
　　在直角坐标系中，画出线段AB,其中A(6，3)，B(6，0). 再以原点O为位似中心，相似比为 ，把线段AB缩小.
在直角坐标系中画出位似图形
①画出线段AB②连接位似中心O③找 的对应点
还有满足条件的线段吗？
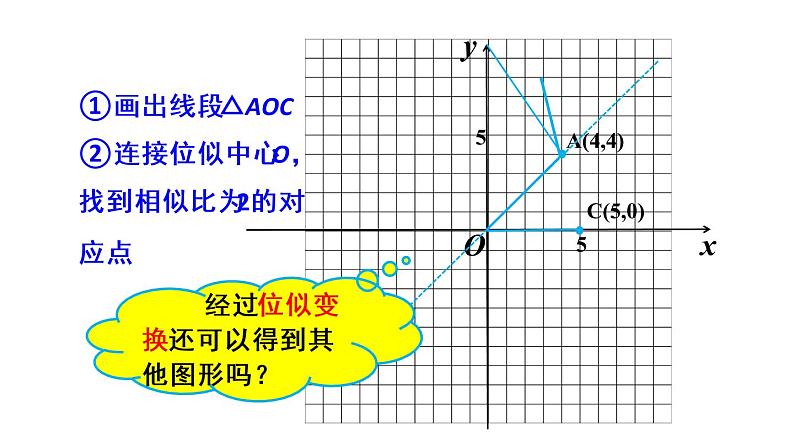
　　在直角坐标系中，△AOC 的三个顶点的坐标分别为A(4,4), O(0,0)，C(5,0).以点O为位似中心，相似比为2，将△AOC放大.
①画出线段△AOC②连接位似中心O，找到相似比为2的对应点
经过位似变换还可以得到其他图形吗？
当以原点为位似中心的两位似图形位于原点同侧时，对应点的坐标有什么变化？
当以原点为位似中心的两位似图形位于原点异侧时，对应点的坐标有什么变化？
（-kx , -ky）
一般地，在平面直角坐标系中，如果以原点为位似中心，新图形与原图形的相似比为k，那么与原图形上的点（x，y）对应的位似图形上的点的坐标为（kx，ky）或（-kx，-ky）.
还可以得到其他图形吗？
1.如图表示△AOB和把它缩小后得到的△OCD，求△AOB与△COD的相似比。
解：相似比为OB:OD=5：2.
2.如图，△ABO三个顶点的坐标分别为A(4,-5), B(6,0), O(0,0). 以原点O为位似中心，把这个三角形放大为原来的2倍，得到△A′B′O′.写出△A′B′O′三个顶点的坐标.
A(4,-5), B(6,0)
A′(8,-10), B′(12,0)
A″(-8,10), B″(-12,0)
至此，我们已经学习了平移、轴对称、旋转和位似等图形的变化方式.你能在下图所示的图案中找到它们吗？
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y 轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
一个图形绕原点旋转180° ,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数
当以原点为位似中心时,变换前后两个图形对应点的横坐标、纵坐标之比的绝对值等于相似比
1.某学习小组在讨论“变化的鱼”时, 知道大鱼与小鱼是位似图形(如图所示), 则小鱼上的点(a, b)对应大鱼上的点( ) A.(-2a, -2b)B.(-a, -2b)C.(-2b, -2a)D.(-2a, -b)
2.△ABC三个顶点坐标分别为A(-2，-2)，B(-4，-2)，C(-6，-4)，以原点为位似中心，将△ABC放大后得到的△DEF与△ABC的相似比为2∶1，这时△DEF中点D的坐标是 .
(-4，-4)或(4，4)
3.如图所示, 图中的小方格都是边长为1的正方形, △ABC与△A′B′C′是以O为位似中心的位似图形, 它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)直接写出△ABC与△A′B′C′的相似比;
(3)以位似中心O为坐标原点, 以格线所在直线为坐标轴建立平面直角坐标系, 画出△A′B′C′关于点O 中心对称的△A″B″C″, 并直接写出△A″B″C″各顶点的坐标．
A″(6,0)，B″(3，-2)，C″(4，-4).
1、在平面直角坐标系中，如果位似变换是以 为位似中心，相似比为k，那么位似图形对应点的坐标的比等于 或 .
2、学习反思：______________________ ______________________________________________________________ .
你有什么感悟与同伴一起分享吧！
位似与平移、轴对称、旋转三种变换的联系和区别:
联系:位似、平移、轴对称、旋转都是图形变换的基本形式;
区别:平移、轴对称、旋转三种图形变换都是全等变换,而位似变换是相似(扩大或缩小)变换．