2021学年27.2.1 相似三角形的判定授课ppt课件

这是一份2021学年27.2.1 相似三角形的判定授课ppt课件，共14页。PPT课件主要包含了学习目标，温故知新，知识讲解，证明∵，即学即练，随堂练习等内容，欢迎下载使用。

1.复习上节课学习的三角形相似的判定方法.2.通过探索，掌握相似三角形的判定定理，并能运用相似三角形的判定定理解决数学问题．
什么叫做相似三角形？什么叫做相似三角形的相似比？ 对应角相等、对应边成比例的三角形叫相似三角形．对应边的比叫做相似三角形的相似比．
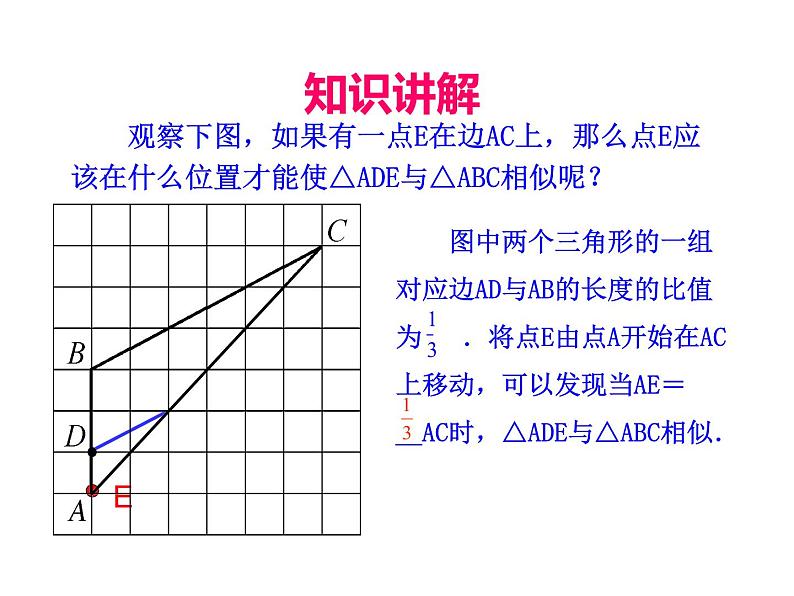
图中两个三角形的一组对应边AD与AB的长度的比值为 ．将点E由点A开始在AC上移动，可以发现当AE＝__AC时，△ADE与△ABC相似．
观察下图，如果有一点E在边AC上，那么点E应该在什么位置才能使△ADE与△ABC相似呢？
猜想：如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似吗？
利用刻度尺和量角器画两个三角形，使它们的两条对应边成比例，并且夹角相等．量一量第三条对应边的长，计算它们的比与前两条对应边的比是否相等．另两个角是否对应相等？你能得出什么结论？
结论：两边成比例且夹角相等的两个三角形相似．
【例1】证明：图中△AEB和△FEC相似．
∴△AEB∽△FEC（两边成比例且夹角相等的两个三角形相似）．
∵　∠AEB＝∠FEC，
下列各组条件中不能使△ABC与△DEF相似的是（ ）（A）∠A=∠D=40° ∠B=∠E=60°（B）∠A=∠D=60° ∠B= 40° ∠E=80° （C）∠A=∠D=50° AB=3 AC=5 DE=6 DF=10 （D）∠B=∠E=70° AB:DE=AC:DF 注意：对应相等的角必须是成比例的两边的夹角，如果不是夹角，它们不一定相似．
1．（烟台·中考）如图，在△ABC中，点D在线段BC上，且△ABC∽△DBA，则下列结论一定正确的是（ ）A.AB2=BC·BD B.AB2=AC·BD C.AB·AD=BD·BC D.AB·AD=AD·CD
2．（吉林·中考）如图，在△ABC中，∠C=90°，D是AC上一点，DE⊥AB于点E，若AC=8，BC=6，DE=3，则AD的长为（ ）
A．3 B．4C．5 D．6
3.已知：如图，△ABC中，P是AB边上的一点，连接CP．试增添一个条件使△ ACP∽△ABC．【解析】 ⑴∵∠A=∠A，∴当∠1=∠ACB (或∠2=∠B)时,△ACP∽△ABC.⑵ ∵∠A=∠A，∴当AC︰AP＝AB︰AC时， △ ACP∽△ABC.答：增添的条件可以是∠1= ∠ACB 或∠2= ∠B 或AC︰AP＝AB︰AC.
4.如图△ABC中，D，E是AB，AC上的点，AB＝7.8，AD＝3，AC＝6，CE＝2.1，试判断△ADE与△ABC是否会相似，小张同学的判断理由是这样的：解析：∵ AC＝AE+CE，而AC＝6，CE＝2.1,∴ AE＝6-2.1＝3.9.由于 ∴ △ADE与△ABC不会相似．你同意小张同学的判断吗?请你说说理由．
【解析】不同意. ∵AC＝AE+CE，而AC＝6，CE＝2.1， ∴ AE＝6-2.1＝3.9 ，∴ AE:AB =3.9:7.8=1:2，AD:AC =3:6=1:2，∴ AE:AB =AD:AC，又 ∵∠A=∠A， ∴ △ADE∽△ACB．