





数学九年级下册27.2.1 相似三角形的判定示范课课件ppt
展开1.能用符号表示两个三角形相似,能确定它们的相似比、对应边和对应角. 2. 能叙述平行线分线段成比例定理及其推论,并能结合图形写出正确的比例式. 3.能用平行线分线段成比例定理的推论证明三角形相似的判定引理.
问题1:我们学过哪些判定两个三角形全等的方法?
SSS,SAS,ASA,AAS
问题2:类比上面这些方法,猜一猜判定两个三角形相似的方法有哪些?
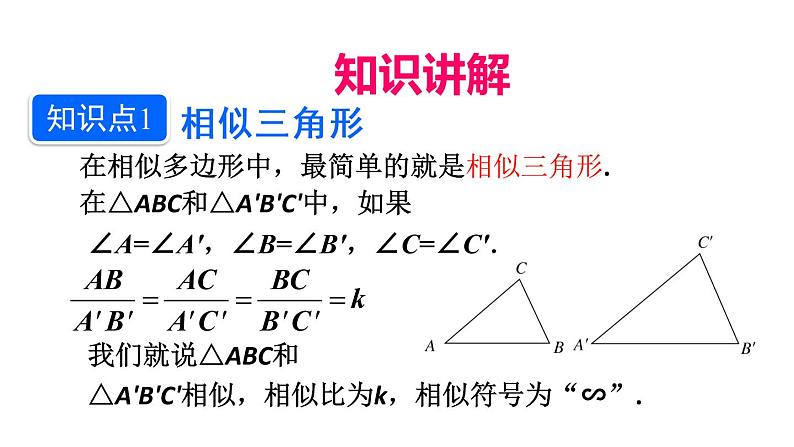
在相似多边形中,最简单的就是相似三角形.
∠A=∠A',∠B=∠B',∠C=∠C'.
在△ABC和△A'B'C'中,如果
我们就说△ABC和△A'B'C'相似,相似比为k,相似符号为“∽”.
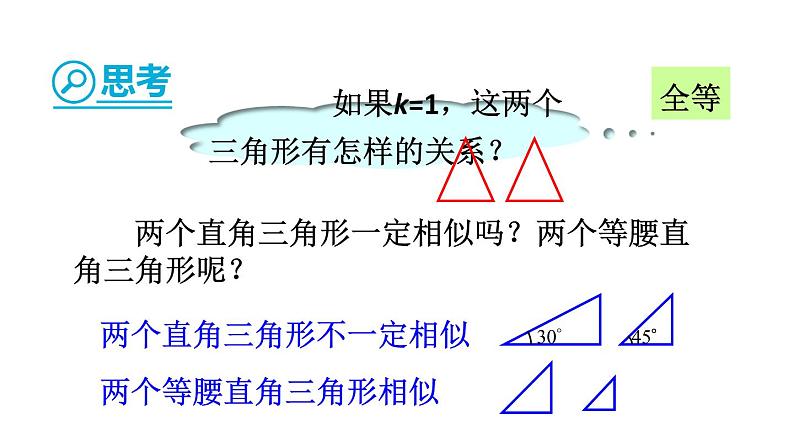
如果k=1,这两个三角形有怎样的关系?
两个直角三角形一定相似吗?两个等腰直角三角形呢?
两个直角三角形不一定相似
两个等腰直角三角形相似
两个等腰三角形一定相似吗?两个等边三角形呢?
判定两个三角形全等时,除了可以验证它们所有的角和边分别相等外,还可以使用简便的判定方法(SSS,SAS,ASA,AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?我们先来探究下面的问题.
可以发现,当l3∥l4∥l5时,有
一般地,我们有平行线分线段成比例的基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
把平行线分线段成比例的基本事实应用到三角形中,会出现下面两种情况:
在图1中,把l4看成平行于△ABC的边BC的直线;在图2中,把l3看成平行于△ABC的边BC的直线,那么我们可以得到结论:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
两条直线被一组平行线所截,所得的对应线段成比例.
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
如图l1∥l2∥l3,试根据图形写出成比例线段.
2.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求 的值.
解:∵AB∥CD∥EF,
如图,在△ABC中,DE∥BC,且DE分别交AB,AC,于点D,E,△ADE与△ABC有什么关系?
证明:在△ADE与△ABC中,∠A= ∠A,∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.过点E作EF∥AB,交BC于点F,∵DE∥BC,EF∥AB,∴ , ∵四边形DBFE是平行四边形,∴DE=BF, ,∴ ∴△ADE∽△ABC
这样,我们证明了△ADE和△ABC相似,因此我们有如下判定三角形相似的定理:
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
如图, DE∥BC分别交BA、CA的延长线于点D、E,那么△ADE与△ABC相似吗?
证明: DE∥BC,∠E=∠C,∠B=∠D,过E作EF∥BD交CB的延长线于F,∵DE∥BC,EF∥BD,∴又∵四边形BDEF是平行四边形,∴DE=BF∴ ∴△ADE∽△ABC
1.如图,在△ABC中,DE∥BC,且AD=3,DB=2.图中的相似三角形是________________,其相似比是____.
2.如图,DE∥BC,DF∥AC,则图中相似三角形一共有( )
A.1对 B.2对 C.3对 D.4对
1.如图,DE∥BC, ,则 ( )
2.如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A. B.C. D.
3.如图,△ABC∽△DCA,AD∥BC,∠B=∠DCA.(1)写出对应边的比例式;(2)写出所有相等的角;(3)若AB=10,BC=12,CA=6,求AD、DC的长.
(2)∠BAC=∠CDA,∠B=∠ACD,∠ACB=∠DAC;
(3)由(1)中的结论和已知条件可知
求得AD=3,DC=5.
4.如图,在△ABC中,DE∥BC分别交AB、AC于点D、E,试证明:
证明:∵DE∥BC,∴△ADE∽△ABC,△DOE∽△COB,∴ ,
初中数学人教版九年级下册27.2.1 相似三角形的判定课文内容课件ppt: 这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定课文内容课件ppt,共17页。PPT课件主要包含了相似多边形概念,相似多边形特征,相似比概念,相似多边形对应边的比,△ADE∽△ABC等内容,欢迎下载使用。
九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定示范课ppt课件: 这是一份九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定示范课ppt课件,共42页。
数学九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定背景图ppt课件: 这是一份数学九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定背景图ppt课件,共42页。













