数学九年级下册第二十八章 锐角三角函数28.1 锐角三角函数说课课件ppt

这是一份数学九年级下册第二十八章 锐角三角函数28.1 锐角三角函数说课课件ppt，共25页。PPT课件主要包含了学习目标，新课导入，知识讲解，知识点1，即学即练，知识点2，知识点3，sin键，输入角度值18°，得到sin18°结果等内容，欢迎下载使用。
1.经历探索30°,45°,60°角的三角函数值的过程，能够进行有关的推理，进一步体会三角函数的意义. 2.能够进行30°,45°,60°角的三角函数值的计算. 3.能够根据30°,45°,60°角的三角函数值说明相应的锐角的大小.
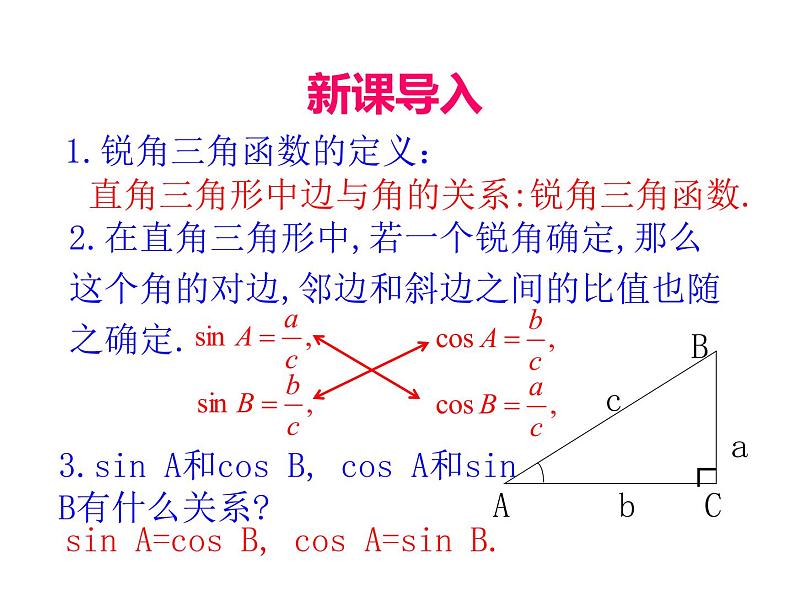
2.在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
直角三角形中边与角的关系:锐角三角函数.
3.sin A和cs B, cs A和sin B有什么关系?
sin A=cs B, cs A=sin B.
1.锐角三角函数的定义：
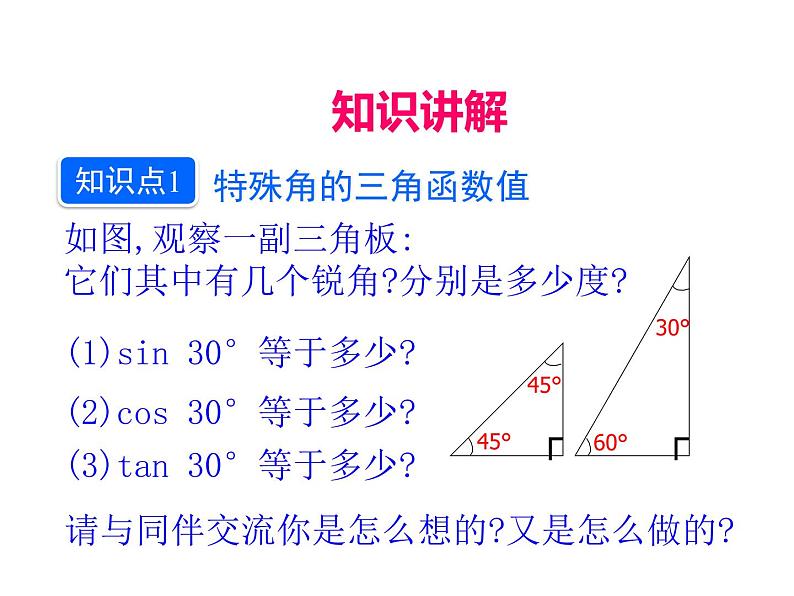
如图,观察一副三角板:它们其中有几个锐角?分别是多少度?
(1)sin 30°等于多少?
(2)cs 30°等于多少?
(3)tan 30°等于多少?
请与同伴交流你是怎么想的?又是怎么做的?
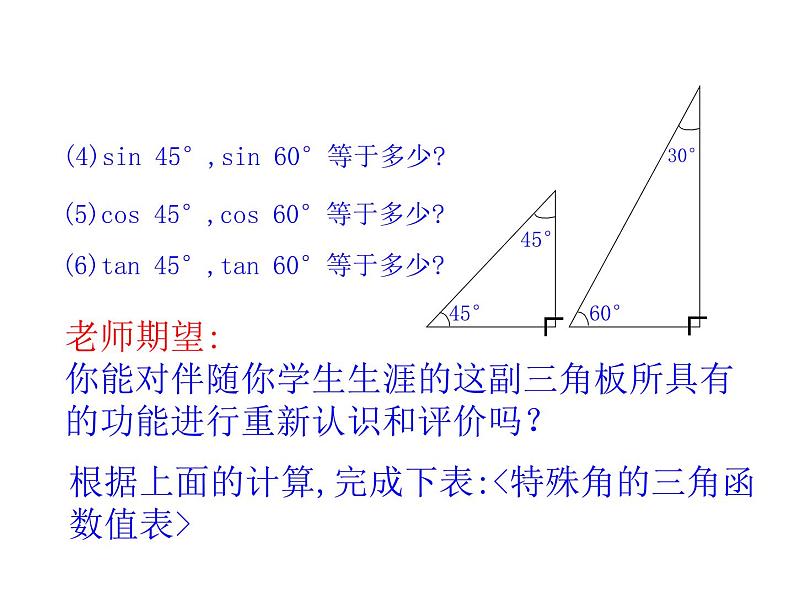
(4)sin 45°,sin 60°等于多少?
(5)cs 45°,cs 60°等于多少?
(6)tan 45°,tan 60°等于多少?
根据上面的计算,完成下表:
老师期望:你能对伴随你学生生涯的这副三角板所具有的功能进行重新认识和评价吗？
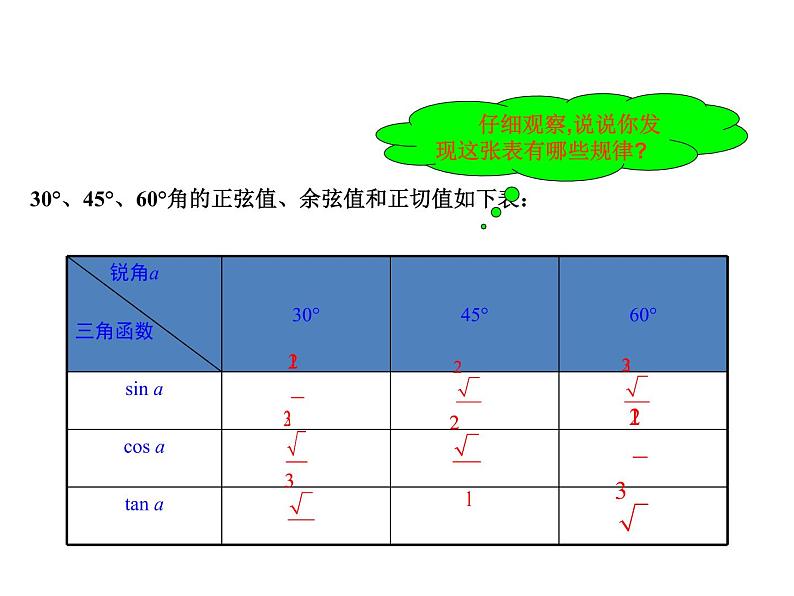
30°、45°、60°角的正弦值、余弦值和正切值如下表：
仔细观察,说说你发现这张表有哪些规律?
例1 求下列各式的值：（1）cs260°＋sin260°（2）
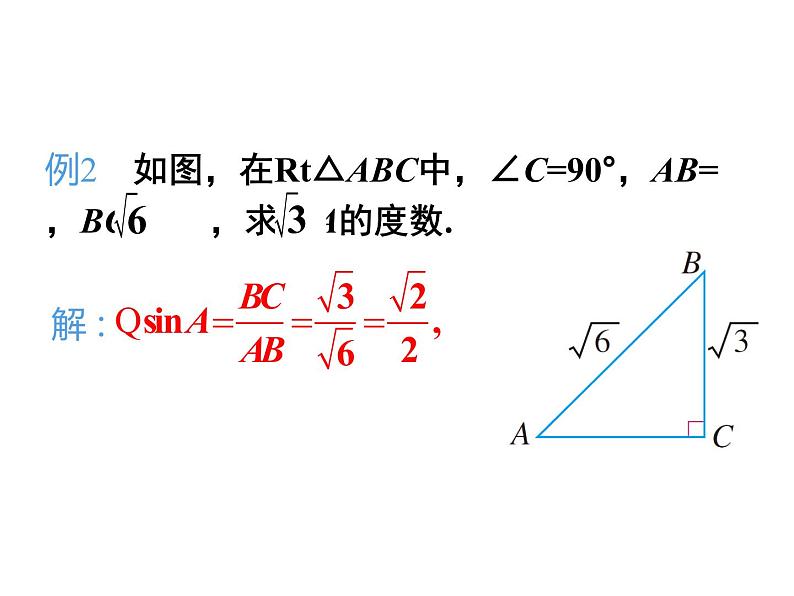
例2 如图，在Rt△ABC中，∠C=90°，AB= ，BC= ，求∠A的度数.
解 :
(1)sin 60°-cs 45°. (2)cs 60°+tan 60°.
2.某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少?
【解析】如图所示,BC=7m， ∠A=30°
∴AB=14 m.即扶梯的长度为14 m.
解: (1)在图(1)中, ∠A＝________(2)在图(2)中.∴α＝ _______
温馨提示：当A，B，为锐角时，若A≠B，则sinA____sinB，csA___csB，tanA____tanB.
反思小结：已知锐角的三角函数值求锐角，关键是熟记特殊角的三角函数值．
在Rt△ABC中，∠C＝90°， 求∠A、∠B的度数．
∠B = 90°－ ∠ A = 90°－30°= 60°
思考：如果锐角A不是这些特殊角时，怎样得到它的三角函数值呢？
非特殊角的三角函数值的求取
试着用计算器求出下面的三角函数值。（1）sin18°; （2）tan30°36'.
0.309016994
0.591398351
以求sin18°为例.
以求tan30°36'为例.
输入角度值30°36'或将其化为30.6°
得到tan30°36'结果
若已知某锐角的三角函数值，能否用计算器求出该锐角的度数呢？
若sin A=0.5018.
输入函数值0.5018
用计算器求下列锐角三角函数值：（1）sin20°，cs70°；sin35°，cs55° ； sin15°32′，cs74°28′（2）tan3°8′，tan80°25′43″；
观察(1)题的结果，你能得出什么猜想？
(1)sin20°≈0.3420，cs70°≈0.3420. sin35°≈0.5736，cs55°≈0.5736. sin15°32′≈0.2678，cs74°28′≈0.2678；(2)tan3°8′≈0.0547， tan80°25′43″≈5.9304.
从（1）的结果可以看出：一个锐角的正弦值等于它的余角的余弦值.
1、已知α为锐角，且 ＜csα＜ ，则α的取值范围是（ ）A．0°