高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线第二课时教学设计

这是一份高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线第二课时教学设计，文件包含精品高中数学新同步精讲讲练322双曲线第二课时精练选择性必修第一册学生版docx、精品高中数学新同步精讲讲练322双曲线第二课时精练选择性必修第一册教师版含解析docx、精品高中数学新同步精讲讲练322双曲线第二课时精讲选择性必修第一册学生版docx、精品高中数学新同步精讲讲练322双曲线第二课时精讲选择性必修第一册教师版含解析docx等4份教案配套教学资源，其中教案共40页， 欢迎下载使用。
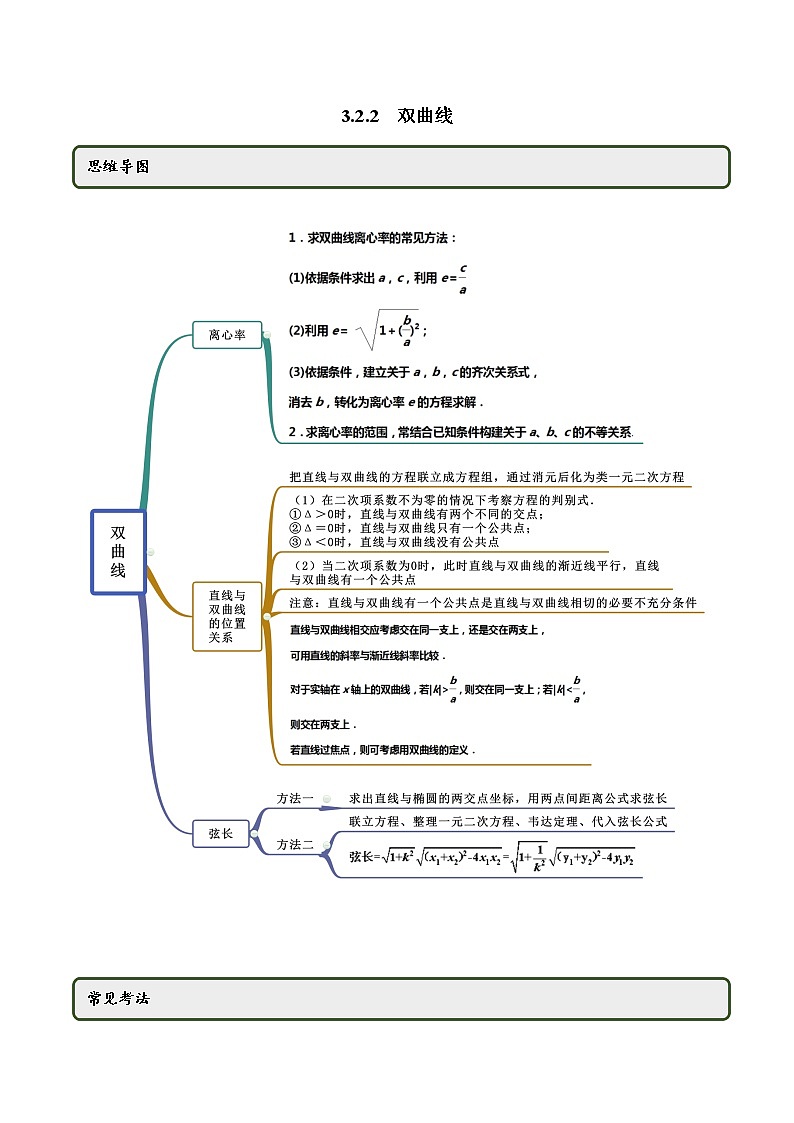
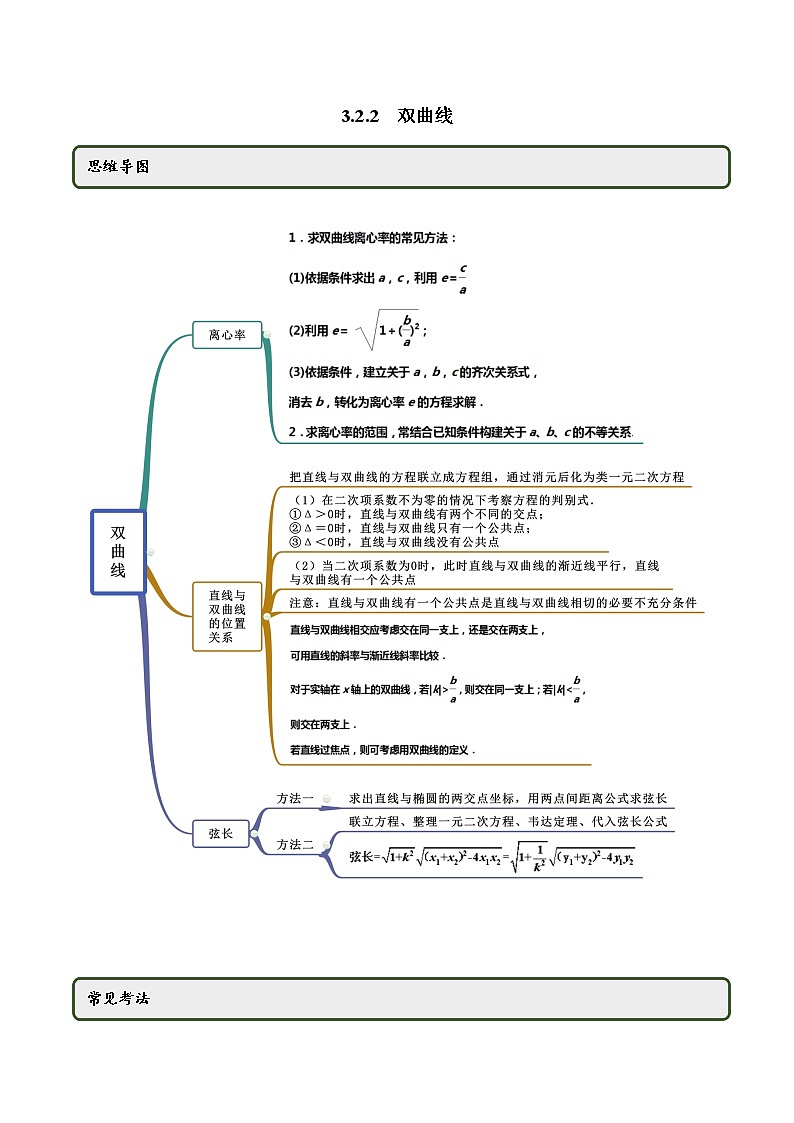
3.2.2  双曲线  考点一 双曲线的离心率【例1】(2020·云南省下关第一中学高二月考)若实数数列：1，，81成等比数列，则圆锥曲线的离心率是(    )A．或 B．或 C． D．或10【答案】A【解析】由1，，81成等比数列有：，所以，当时，方程为，表示焦点在y轴的椭圆，其中，，故离心率；当时，方程为，表示焦点在x轴的双曲线，其中，，故离心率,故选择A.【举一反三】1．(2020·江苏南京)在平面直角坐标系xOy中，若点P(，0)到双曲线C：的一条渐近线的距离为6，则双曲线C的离心率为(    )A．2 B．4 C． D．【答案】A【解析】双曲线C：的一条渐近线为，则，解得，.故选：A.2．(2020·贵州省思南中学高二期末(理))已知、为双曲线：的左、右焦点，点为双曲线右支上一点，，，则双曲线的离心率为(    )A． B． C． D．【答案】C【解析】根据题意作图如下：设.∵∴∵由双曲线焦半径公式知，∴∴故选C.3．(2020·全国)已知，为双曲线的焦点，为与双由线的交点，且有，则该双曲线的离心率为(    )A． B． C． D．【答案】C【解析】由题意知，在中，，可设，则，由勾股定理得，，又由得，所以.故选：C4．(2020·沙坪坝.重庆八中高二月考)若双曲线(，)的一条渐近线经过点，则该双曲线的离心率为(    )A． B． C． D．【答案】C【解析】双曲线的一条渐近线经过点，点在直线上，．则该双曲线的离心率为.故选：．考点二  直线与双曲线的位置关系【例2】已知双曲线x2－＝1，问当直线l的斜率k为何值时，过点P(1,1)的直线l与双曲线只有一个公共点．【答案】见解析【解析】①当直线l的斜率不存在时，直线l：x＝1与双曲线相切，符合题意．②当直线l的斜率存在时，设直线l的方程为y＝k(x－1)＋1，代入双曲线方程，得(4－k2)x2－(2k－2k2)x－k2＋2k－5＝0.当4－k2＝0，即k＝±2时，直线l与双曲线的渐近线平行，直线l与双曲线只有一个公共点．当4－k2≠0时，令Δ＝0，得k＝.综上可知，当k＝或k＝±2或直线l的斜率不存在时，过点P的直线l与双曲线都只有一个公共点．【举一反三】1．(2018·福建高二期末(理))若直线与双曲线的右支交于不同的两点，则的取值范围是　　A． B．C． D．【答案】D【解析】把y＝kx＋2代入x2－y2＝6，得x2－(kx＋2)2＝6，化简得(1－k2)x2－4kx－10＝0，由题意知即解得＜k＜－1.答案：D.2．(2020·天水市第一中学高二月考(理))直线：与双曲线：的右支交于不同的两点，则斜率的取值范围是()A． B． C． D．【答案】C【解析】由 可得， ，因为直线与双曲线交于不同的两点，所以， 解得 ，所以斜率的取值范围是，故选C. 3．(2020·四川资阳)直线l：kx－y－2k＝0与双曲线x2－y2＝2仅有一个公共点，则实数k的值为A．－1或1 B．－1C．1 D．1，－1，0【答案】A【解析】因为直线l：kx－y－2k＝0过定点(2,0),而直线l：kx－y－2k＝0与双曲线x2－y2＝2仅有一个公共点，所以直线l：kx－y－2k＝0与双曲线渐近线平行，即实数k的值为－1或1，选A.4．(2020·宁波市北仑中学高一期中)过双曲线2x2－y2＝2的右焦点作直线l交双曲线于A，B两点，若|AB|＝4，则这样的直线l的条数为(　　)A．1 B．2C．3 D．4【答案】C【解析】设，当直线与轴垂直时，，满足题意当直线与轴不垂直时，设直线：，联立直线与双曲线方程得：，整理得：，所以， ，又=，解得：，综上：满足这样的直线l的条数为3条考点三 弦长【例3】(2019·全国高三课时练习)过双曲线的右焦点F2，倾斜角为30°的直线交双曲线于A，B两点，O为坐标原点，F1为左焦点．(1)求|AB|；(2)求△AOB的面积．【答案】(1)；(2).【解析】(1)由双曲线的方程得，∴，F1(－3，0)，F2(3，0)．直线AB的方程为．设A(x1，y1)，B(x2，y2)，由消去y得5x2＋6x－27＝0.∴，.∴(2)直线AB的方程变形为.∴原点O到直线AB的距离为.∴.【举一反三】1．(2020·全国)已知直线y＝kx＋1与双曲线交于A，B两点，且|AB|＝8，则实数k的值为(　　)A．± B．±或±C．± D．±【答案】B【解析】由直线与双曲线交于两点，得，将代入得，则，即.设，，则，.∴∴或.故选B.2．(2018·全国高二课时练习)求双曲线被直线截得的弦长              .【答案】【解析】由，得，即．    (*)设方程(*)的解为，，则有，，故．3．(2020·邢台市第八中学高二期末)已知双曲线C：的离心率为，点是双曲线的一个顶点．(1)求双曲线的方程；(2)经过双曲线右焦点F2作倾斜角为30°的直线，直线与双曲线交于不同的两点A，B，求.【答案】(1)；(2)【解析】(1)因为双曲线C：的离心率为，点是双曲线的一个顶点，所以解得，所以双曲线的方程为(2)双曲线的右焦点为所以经过双曲线右焦点F2且倾斜角为30°的直线的方程为．联立得.设，则.所以.4．(2020·宾县第二中学高二期末(文))已知曲线及直线．(1)若与左支交于两个不同的交点，求实数的取值范围；(2)若与交于两点，是坐标原点，且的面积为，求实数的值．【答案】(1)；(2)或【解析】(1)由消去，得．∵与左支交于两个不同的交点∴且∴的取值范围为(2)设，由(1)得．又过点，∴．∴，即．∴或．   考点四 点差法【例4】(1)(2020·黑龙江南岗)已知双曲线：，斜率为2的直线与双曲线相交于点、，且弦中点坐标为，则双曲线的离心率为(    )A．2 B． C． D．3(2)(2020·河南南阳.高二其他(文))直线经过且与双曲线交于，两点，如果点是线段的中点，那么直线的方程为(    )A． B．C． D．不存在(3)(2019·黑龙江大庆四中高二月考(理))已知双曲线与不过原点且不平行于坐标轴的直线相交于两点，线段的中点为，设直线的斜率为，直线的斜率为，则A． B． C． D．【答案】(1)B(2)A(3)A【解析】(1)设、，则，，所以，所以，又弦中点坐标为，所以，，又，所以，即，所以双曲线的离心率.故选：B.(2)当斜率不存在时，显然不符合题意；当斜率存在时，设，，因为点是线段的中点，所以，，代入双曲线方程得，两式相减得，则，又直线过点P，所以直线方程为，联立，得到，经检验，方程有解，所以直线满足题意.故选：A(3)设直线l的方程为，代入双曲线方程得到，得到设，则则，故，故选A．【举一反三】1．(2020·青海西宁)已知倾斜角为的直线与双曲线C：(，)相交于A，B两点，是弦的中点，则双曲线的离心率为(    )A． B． C． D．【答案】D【解析】因为倾斜角为的直线与双曲线C：(，)相交于A，B两点，所以直线的斜率，设，则①②由①②得则因为是弦的中点，因为直线的斜率为1即所以，则，故选：D2．(2020·湖北武汉)已知分别为双曲线实轴的左右两个端点，过双曲线的左焦点作直线交双曲线于两点(点异于)，则直线的斜率之比(    )A． B． C． D．【答案】B【解析】由已知得双曲线，，．故，，．设直线，且，，，．由消去整理得，，两式相比得①，②，将①代入②得：上式．故．故选：B．3．(2019·会泽县第一中学校高二月考(理))点 平分双曲线 的一条弦，则这条弦所在直线的方程是__________．【答案】【解析】设弦的两端点分别为的中点是 把代入双曲线 得 ，∴ ∴这条弦所在的直线方程是 故答案为．