初中数学人教版八年级上册第十一章 三角形综合与测试单元测试精练

这是一份初中数学人教版八年级上册第十一章 三角形综合与测试单元测试精练，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列说法正确的是（ ）
A． 三角形分为等边三角形和三边不相等的三角形
B． 等边三角形不是等腰三角形
C． 等腰三角形是等边三角形
D． 三角形分为锐角三角形，直角三角形，钝角三角形
2.如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=24°，则∠BDC等于（ ）
A． 42°
B． 66°
C． 69°
D． 77°
3.一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数为（ ）
A． 7
B． 8
C． 9
D． 10
4.如图，在△BDF和△ABC中，它们相同的角是（ ）
A． ∠A
B． ∠C
C． ∠ABC
D． ∠ACB
5.如图，AB∥CD，AD与BC相交于点O，已知角α、β，则用角α、β表示∠AOC，则∠AOC=（ ）
A．α+β
B． 180°-α+β
C． 2α-β
D． 180°+α-β
6.若三角形的三边长分别为3，4，x，则x的值可能是（ ）
A． 1
B． 6
C． 7
D． 10
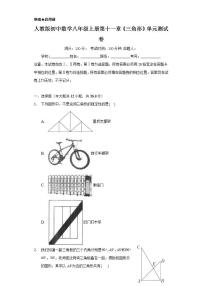
7.如图所示的图形中，属于多边形的有（ ）个．
A． 3个
B． 4个
C． 5个
D． 6个
8.如图，△ABC中，∠1=∠2，∠3=∠4，若∠D=25°，则∠A=（ ）
A． 25°
B． 65°
C． 50°
D． 75°
9.适合条件∠A=∠B=∠C的三角形一定是（ ）
A． 锐角三角形
B． 钝角三角形
C． 直角三角形
D． 任意三角形
10.八边形的内角和是（ ）
A． 1440°
B． 1080°
C． 900°
D． 720°
11.如图，点D在BC的延长线上，连接AD，则∠EAD是（ ）的外角.
A． △ABC
B．△ACD
C． △ABD
D． 以上都不对
12.如图，在△ABC中，EF∥AC，BD⊥AC，BD交EF于G，则下面说法中错误的是（ ）
A．BD是△BDC的高
B．CD是△BCD的高
C．EG是△BEF的高
D．BE是△BEF的高
二、填空题
13.一副三角板，如图所示叠放在一起，则图中∠α的度数是．
14.如图，点D、E为△ABC边BC、AC上的两点，将△ABC沿线段DE折叠，点C落在BD上的C′处，
若∠C=30°，则∠AEC′=．
15.如图，写出△ADE的外角.
16.在图中过点P任意画一条直线，最多可以得到____________个三角形.
17.如图，已知∠A=30°，∠B=40°，∠C=50°，那么∠AOB=度．
三、解答题
18.如图，点D是△ABC的边BC上的一点，∠B=∠BAD=∠C，∠ADC=72°．试求∠DAC的度数．
19.如图，已知AB∥CD，EF与AB、CD分别相交于点E、F，∠BEF与∠EFD的平分线相交于点P，求证：△EPF为直角三角形．
20.多边形的内角和随着边数的变化而变化．设多边形的边数为n，内角和为N，则变量N与n之间的关系可以表示为N=（n-2）•180°．例如：如图四边形ABCD的内角和：N=∠A+∠B+∠C+∠D=（4-2）×180°=360°问：（1）利用这个关系式计算五边形的内角和；（2）当一个多边形的内角和N=720°时，求其边数n．
21.已知：在△ABC中，∠BAC=90°，AD⊥BC于点D，∠ABC的平分线BE交AD于F，试说明∠AEF=∠AFE．
22.已知凸四边形ABCD中，∠A=∠C=90°．（1）如图1，若DE平分∠ADC，BF平分∠ABC的邻补角，判断DE与BF位置关系并证明；（2）如图2，若BF、DE分别平分∠ABC、∠ADC的邻补角，判断DE与BF位置关系并证明．
答案解析
1.【答案】D
【解析】A．三角形分为等腰三角形和三边不相等的三角形，故本选项错误，
B．等边三角形是等腰三角形，故本选项错误，
C．等腰三角形不一定是等边三角形，故本选项错误，
D．三角形分为锐角三角形，直角三角形，钝角三角形，故本选项正确，
故选D．
2.【答案】C
【解析】在△ABC中，∠ACB=90°，∠A=24°，∴∠B=90°-∠A=66°．由折叠的性质可得：∠BCD=∠ACB=45°，∴∠BDC=180°-∠BCD-∠B=69°．故选C．
3.【答案】A
【解析】设这个多边形的边数为n，根据题意得，（n-2）•180°=360°×2+180°，解得n=7．故选A．
4.【答案】C
【解析】△BDF的角有∠D，∠DBF，∠DFB；△ABC的角有∠A，∠ACB，∠ABC；它们相同的角是∠ABC.
5.【答案】A
【解析】∵AB∥CD，∴∠ABO=β．在△AOB中，利用三角形的外角性质得到∠AOC=∠A+∠ABO=α+β．故选A．
6.【答案】B
【解析】∵4﹣3=1，4+3=7，
∴1＜x＜7，
∴x的值可能是6．
故选B．
7.【答案】A
【解析】根据多边形的定义：平面内不在同一条直线上的几条线段首尾顺次相接组成的图形叫多边形．显然只有第一个、第二个、第五个．故选A
8.【答案】C
【解析】∵BD是∠ABC的平分线，∴∠DBC=∠ABC，∵CD是△ABC的外角平分线，∴∠ACD=（∠A+∠ABC），∵∠D+∠DBC+∠ACB+∠ACD=180°，
即∠ABC+∠ACB+（∠A+∠ABC）=155°①，
∠A+∠ABC+∠ACB=180°②，∴∠ABC+∠ACB=130°，∴∠A=50°．故选C．
9.【答案】B
【解析】设∠A=x°，则∠B=x°，∠C=3x°．根据三角形的内角和定理，得x+x+3x=180，x=36．则∠C=108°．则该三角形是钝角三角形．故选B．
10.【答案】B
【解析】由题意得：180°（8-2）=1080°，故选B．
11.【答案】C
【解析】根据三角形的一边与另一边的延长线组成的角叫做三角形的外角，图中∠EAD是△ABD的外角，所以正确的选项是C.
12.【答案】D
【解析】A.BD⊥AC，则BD是△BDC的高，故命题正确；
B.CD⊥BD，则CD是△BCD的高，故命题正确；
C.EG⊥BG，则EG是△BEF的高，故命题正确；
D.错误；
13.【答案】75°
【解析】如图，∠1=45°-30°=15°， ∠α=90°-∠1=90°-15°=75°． 故答案为：75°
14.【答案】60°
【解析】根据折叠可得：EC=EC′， ∴∠EC′D=∠C，
∵∠C=30°， ∴∠EC′D=30°，
∴∠AEC′=30°+30°=60°， 故答案为：60°．
15.【答案】∠BDF、∠DEC和∠AEF
【解析】根据三角形的一边与另一边的延长线组成的角叫做三角形的外角，
图中符合条件的角是∠BDF、∠DEC和∠AEF.
16.【答案】6
【解析】如图1，有2个三角形；如图2，有4个三角形；如图3，有4个三角形；如图4，有5个三角形；如图5，有6个三角形．综上所述，最多有6个三角形．
17.【答案】120
【解析】延长BO交AC于D， ∵∠B=40°，∠C=50°，
∴∠ADO=40°+50°=90°，
∵∠A=30°， ∴∠AOB=30°+90°=120°， 故答案为：120．
18.【答案】解：∵∠ADC是△ABD的外角，∠ADC=72°，
∴∠ADC=∠B+∠BAD．
又∵∠B=∠BAD，
∴∠B=∠BAD=36°．
∵∠B=∠BAD=∠C，
∴∠C=36°．
在△ADC中，
∵∠DAC+∠ADC+∠C=180°
∴∠DAC=180°-∠ADC-∠C
=180°-72°-36°
=72°．
【解析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD，
再由∠B=∠BAD可知∠B=∠BAD=36°，在△ADC中，
根据三角形内角和定理即可得出结论．
19.【答案】证明：∵AB∥CD， ∴∠BEF+∠EFD=180°，
又EP、FP分别是∠BEF、∠EFD的平分线，
∴∠PEF=∠BEF，∠EFP=∠EFD，
∴∠PEF+∠EFP=（∠BEF+∠EFD）=90°，
∴∠P=180°-（∠PEF+∠EFP）=180°-90°=90°，
∴△EPF为直角三角形.
【解析】要证△EPF为直角三角形，只要证∠PEF+∠EFP=90°，
由角平分线的性质和平行线的性质可知，∠PEF+∠EFP=（∠BEF+∠EFD）=90°．
20.【答案】解：（1）N=（5-2）×180°=540°（2）根据题意得：（n-2）×180°=720°解得n=6．
【解析】（1）将n=5代入公式，依据公式计算即可；（2）将N=720°代入公式，得到关于n的方程，然后求解即可．
21.【答案】证明：∵BE平分∠ABC，∴∠CBE=∠ABE，∵∠BAC=90°，∴∠ABE+∠AEF=90°，∵DA⊥BC，∴∠CBE+∠BFD=90°，∴∠AEF=∠BFD，∵∠BFD=∠AFE（对顶角相等），∴∠AEF=∠AFE
【解析】根据角平分线的定义求出∠ABE=∠EBC，
再利用∠BAC=90°，AD⊥BC于点D推出∠AEF=∠AFE．
22.【答案】解：（1）DE⊥BF，延长DE交BF于点G∵∠A+∠ABC+∠C+∠ADC=360°又∵∠A=∠C=90°，∴∠ABC+∠ADC=180°∵∠ABC+∠MBC=180°∴∠ADC=∠MBC，∵DE、BF分别平分∠ADC、∠MBC∴∠EDC=∠ADC，∠EBG=∠MBC，∴∠EDC=∠EBG，∵∠EDC+∠DEC+∠C=180°∠EBG+∠BEG+∠EGB=180°又∵∠DEC=∠BEG∴∠EGB=∠C=90∴DE⊥BF；（2）DE∥BF，连接BD，∵DE、BF分别平分∠NDC、∠MBC∴∠EDC=∠NDC，∠FBC=∠MBC，∵∠ADC+∠NDC=180°又∵∠ADC=∠MBC∴∠MBC+∠NDC=180°∴∠EDC+∠FBC=90°，∵∠C=90°∴∠CDB+∠CBD=90°∴∠EDC+∠CDB+∠FBC+∠CBD=180°即∠EDB+∠FBD=180°，∴DE∥BF．
【解析】（1）DE⊥BF，延长DE交BF于G．易证∠ADC=∠CBM．可得∠CDE=∠EBF．
即可得∠EGB=∠C=90゜，则可证得DE⊥BF；（2）DE∥BF，连接BD，易证∠NDC+∠MBC=180゜，则可得∠EDC+∠CBF=90゜，
继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜，则可得DE∥BF．