中考数学专题冲刺高分狙击【专题分析＋解题方法＋知识结构＋典例精选＋能力评估检测】：专题七　圆

这是一份中考数学专题冲刺高分狙击【专题分析＋解题方法＋知识结构＋典例精选＋能力评估检测】：专题七　圆，共11页。

圆在中考中的常见考点有圆的性质及定理，圆周角定理及其推论，圆心角、圆周角、弧、弦之间的“等推”关系；切线的判定，切线的性质，切线长定理，弧长及扇形面积的计算，求阴影部分的面积等．对圆的考查在中考中以客观题为主，考查题型多样，关于圆的基本性质一般以选择题或填空题的形式进行考查，切线的判定等综合性强的问题一般以解答题的形式进行考查；圆在中考中的比重约为10%～15%.
【解题方法】
解决圆的有关问题常用的数学思想就是转化思想，方程思想和数形结合思想；常用的数学方法有分类讨论法，设参数法等．
【知识结构】
【典例精选】
如图，⊙O的半径是3，点P是弦AB延长线上的一点，连结OP，若OP＝4，∠APO＝30°，则弦AB的长为( )
A．2eq \r(5) B. eq \r(5)
C．2eq \r(13) D. eq \r(13)
【思路点拨】先过点O作OC⊥AP，连结OB，根据OP＝4，∠APO＝30°，求出OC的值，在Rt△BCO中，根据勾股定理求出BC的值，进而得出AB的值．
【解析】如图，过点O作OC⊥AP于点C，连结OB，∵OP＝4，∠APO＝30°，∴OC＝4×sin 30°＝2.∵OB＝3，∴BC＝eq \r(OB2－OC2)＝eq \r(32－22)＝eq \r(5)，∴AB＝2eq \r(5).故选A.
答案：A
规律方法：
利用垂径定理进行证明或计算，通常是在半径、圆心距和弦的一半所组成的直角三角形中，利用勾股定理构建方程求出未知线段的长.
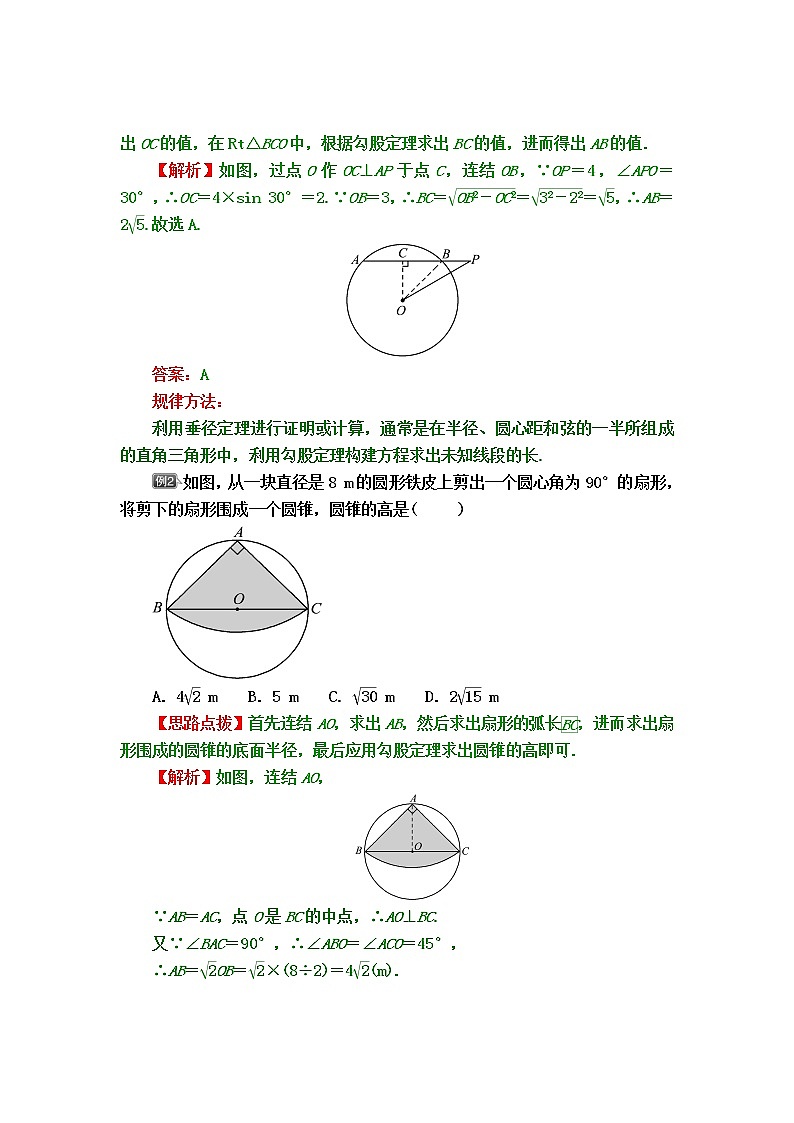
如图，从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，圆锥的高是( )
A．4eq \r(2) m B．5 m C. eq \r(30) m D．2eq \r(15) m
【思路点拨】首先连结AO，求出AB，然后求出扇形的弧长eq \x\t(BC)，进而求出扇形围成的圆锥的底面半径，最后应用勾股定理求出圆锥的高即可．
【解析】如图，连结AO，
∵AB＝AC，点O是BC的中点，∴AO⊥BC.
又∵∠BAC＝90°，∴∠ABO＝∠ACO＝45°，
∴AB＝eq \r(2)OB＝eq \r(2)×(8÷2)＝4eq \r(2)(m)．
∴leq \x\t(BC)＝eq \f(90π×4\r(2),180)＝2eq \r(2)π(m)．
∴将剪下的扇形围成的圆锥形的半径是2eq \r(2)π÷2π＝eq \r(2)(m)．
∴圆锥的高是eq \r(4\r(2)2－\r(2)2)＝eq \r(30)(m)．故选C.
答案：C
规律方法：
解决圆锥的相关问题，可以利用圆的周长等于扇形的弧长建立方程，利用方程解决问题.
如图，在边长为6的正方形ABCD中，E是AB的中点，以E为圆心、ED为半径作半圆，交A，B所在的直线于M，N两点，分别以MD，ND为直径作半圆，则阴影部分的面积为( )
A．9eq \r(5) B．18eq \r(5) C．36eq \r(5) D．72eq \r(5)
【思路点拨】根据图形可知阴影部分的面积＝两个小的半圆的面积＋△DMN的面积－大半圆的面积，MN为半圆的直径，从而可知∠MDN＝90°，在Rt△MDN中，由勾股定理可知MN2＝MD2＋DN2，从而可得到两个小半圆的面积＝大半圆的面积，故此阴影部分的面积＝△DMN的面积，在Rt△AED中，ED＝eq \r(AD2＋AE2)＝eq \r(62＋32)＝3eq \r(5)，所以MN＝6eq \r(5)，然后利用三角形的面积公式求解即可．
【解析】根据图形可知阴影部分的面积＝两个小的半圆的面积＋△DMN的面积－大半圆的面积．∵MN为大半圆的直径，∴∠MDN＝90°.在Rt△MDN中，MN2＝MD2＋DN2，∴两个小半圆的面积和＝大半圆的面积．∴阴影部分的面积＝△DMN的面积．在Rt△AED中，ED＝eq \r(AD2＋AE2)＝eq \r(62＋32)＝3eq \r(5)，∴阴影部分的面积＝△DMN的面积＝eq \f(1,2)MN·AD＝eq \f(1,2)×6eq \r(5)×6＝18eq \r(5).故选B.
答案：B
规律方法：
求阴影部分的面积，一般是将所求阴影部分进行分割组合，转化为规则图形的和或差.
如图，在Rt△ABC中，∠ACB＝90°，以AC为直径作⊙O交AB于点D，连结CD.
(1)求证：∠A＝∠BCD.
(2)若M为线段BC上一点，试问当点M在什么位置时，直线DM与⊙O相切？并说明理由．
【思路点拨】(1)根据圆周角定理可得∠ADC＝90°，根据直角三角形的性质可得∠A＋∠ACD＝90°，再由∠DCB＋∠ACD＝90°，可得∠A＝∠BCD；(2)当点M是BC的中点时，直线DM与⊙O相切．连结DO，证明∠ODM＝90°，进而证得直线DM与⊙O相切．
【自主解答】
(1)证明：∵AC为直径，
∴∠ADC＝90°，∴∠A＋∠ACD＝90°.
∵∠ACB＝90°，∴∠BCD＋∠ACD＝90°，
∴∠A＝∠BCD.
(2)解：当点M是BC的中点时，直线DM与⊙O相切．理由如下：如图，连结DO，
∵DO＝CO，∴∠1＝∠2.
∵∠BDC＝90°，点M是BC的中点，
∴DM＝CM，∴∠4＝∠3.
∵∠2＋∠4＝90°，
∴∠1＋∠3＝90°，
∴直线DM与⊙O相切．
规律方法：
在判定一条直线是圆的切线时，如果这条直线和圆有公共点，常作出经过公共点的半径，证明这条直线与经过公共点的半径垂直，概括为“连半径，证垂直，得切线”.
【能力评估检测】
一、选择题
1．如图，AB是⊙O的直径，点C在⊙O上，AE是⊙O的切线，A为切点，连结BC并延长交AE于点D.若∠AOC＝80°，则∠ADB的度数为( B )
A．40° B．50° C．60° D．20°
2．如图，⊙O是△ABC的外接圆，∠AOB＝60°，AB＝AC＝2，则弦BC的长为( C )
A. eq \r(3) B．3 C．2eq \r(3) D．4
3．如图，在⊙O中，弦AC∥半径OB，∠BOC＝50°，则∠OAB的度数为( A )
A．25° B．50° C．60° D．30°
4.如图，直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C，且AB＝2，AD＝1，P点在切线CD上移动．当∠APB的度数最大时，则∠ABP的度数为( B )
A．15° B．30° C．60° D．90°
5．如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB长为半径的扇形(忽略铁丝的粗细)，则所得扇形DAB的面积为( D )
A．6 B．7 C．8 D．9
6．如图，已知AB为⊙O的直径，AD切⊙O于点A，eq \x\t(EC)＝eq \x\t(CB).则下列结论中不一定正确的是( D )
A．BA⊥DA B．OC∥AE
C．∠COE＝2∠CAE D．OD⊥AC
7．如图，菱形ABCD的对角线BD，AC分别为2，2eq \r(3)，以B为圆心的弧与AD，DC相切，则阴影部分的面积是( D )
A．2eq \r(3)－eq \f(\r(3),3)π B．4eq \r(3)－eq \f(\r(3),3)π
C．4eq \r(3)－π D．2eq \r(3)－π
8．如图，正六边形ABCDEF是边长为2 cm的螺母，点P是FA延长线上的点，在A，P之间拉一条长为12 cm的无伸缩性细线，一端固定在点A，握住另一端点P拉直细线，把它全部紧紧缠绕在螺母上(缠绕时螺母不动)，则点P运动的路径长为( B )
A．13π cm B．14π cm
C．15π cm D．16π cm
9．如图，在矩形ABCD中，AB＝4，AD＝5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线交BC于点M，切点为N，则DM的长为( )
A. eq \f(13,3) B. eq \f(9,2) C. eq \f(4,3)eq \r(13) D．2eq \r(5)
解：如图，连接OE，OF，ON，OG.∵AD，AB，BC分别与⊙O相切于E，F，G三点，∴∠AEO＝∠AFO＝∠OFB＝∠BGO＝90°.∴四边形AFOE，FBGO都是正方形．∴AF＝BF＝AE＝BG＝2.∴DE＝3.∵DM是⊙O的切线，∴DN＝DE＝3，MN＝MG. ∴CM＝5－2－MN＝3－MN.在Rt△DMC中，DM2＝CD2＋CM2，∴(3＋MN)2＝(3－MN)2＋42.∴NM＝eq \f(4,3).∴DM＝3＋eq \f(4,3)＝eq \f(13,3).故选A.
答案：A
二、填空题
10．在平面直角坐标系中，O为坐标原点，则直线y＝x＋eq \r(2)与以O点为圆心，1为半径的圆的位置关系为 相切．
11．如图，圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠A＝55°，∠E＝30°，则∠F＝40° .
12．如图，正三角形ABC的边长为2，点A，B在半径为eq \r(2)的圆上，点C在圆内，将正三角形ABC绕点A逆时针旋转，当点C第一次落在圆上时，点C运动的路线长为 .
【解析】设点C落在圆上的点为C′，连结OA，OB，OC′，则OA＝OB＝eq \r(2).又∵AB＝2，∴OA2＋OB2＝AB2，∴∠AOB＝90°，∴∠OAB＝45°，同理∠OAC′＝45°，∴∠BAC′＝90°.
∵△ABC为等边三角形，∴∠CAB＝60°，∴∠CAC′＝30°，∴点C运动的路线长为eq \f(30π×2,180)＝eq \f(π,3).故答案为eq \f(π,3).
答案：eq \f(π,3)
13．如图，在△ABC中，∠BAC＝90°，AB＝5 cm，AC＝2 cm，将△ABC绕顶点C
按顺时针方向旋转45°至△A1B1C的位置，则线段AB扫过区域(图中的阴影部分)的面积为 cm2.
【解析】在Rt△ABC中，BC＝eq \r(AC2＋AB2)＝eq \r(29)(cm)，
S扇形BCB1＝eq \f(45π×\r(29)2,360)＝eq \f(29π,8)(cm2)，S△CB1A1＝eq \f(1,2)×5×2＝5(cm2)，S扇形CAA1＝eq \f(45π×22,360)＝eq \f(π,2)(cm2)，故S阴影部分＝S扇形BCB1＋S△CB1A1－S△ABC－S扇形CAA1＝eq \f(29π,8)＋5－5－eq \f(π,2)＝eq \f(25π,8)(cm2).
答案：eq \f(25π,8)
三、解答题
14．如图，AB是⊙O的直径，BC切⊙O
于点B，OC平行于弦AD，过点D作DE⊥AB于点E，连结AC，与DE交于点P.求证：
(1)PE＝PD；
(2)AC·PD＝AP·BC.
证明：(1)∵AB是⊙O的直径，BC是切线，∴AB⊥BC，∵DE⊥AB，∴DE∥BC，∴△AEP∽△ABC，∴eq \f(EP,BC)＝eq \f(AE,AB).又∵AD∥OC，∴∠DAE＝∠COB，∴△AED∽△OBC，∴eq \f(ED,BC)＝eq \f(AE,OB)＝eq \f(AE,\f(1,2)AB)＝eq \f(2AE,AB).∴ED＝2EP，∴PE＝PD.
(2)∵AB是⊙O的直径，BC是切线，∴AB⊥BC，∵DE⊥AB，∴DE∥BC，∴△AEP∽△ABC，∴eq \f(AP,AC)＝eq \f(PE,BC).∵PE＝PD，∴eq \f(AP,AC)＝eq \f(PD,BC)，∴AC·PD＝AP·BC.
15．如图，在△OAB中，OA＝OB＝10，∠AOB＝80°，以点O为圆心，6为半径的优弧eq \x\t(MN)分别交OA，OB于点M，N.
(1)点P在右半弧上(∠BOP是锐角)，将OP绕点O逆时针旋转80°得OP′，求证：AP＝BP′；
(2)点T在左半弧上，若AT与弧相切，求点T到OA的距离；
(3)设点Q在优弧eq \x\t(MN)上，当△AOQ的面积最大时，直接写出∠BOQ的度数．
(1)证明：如图，∵∠AOP＝∠AOB＋∠BOP＝80°＋∠BOP，∠BOP′＝∠POP′＋∠BOP＝80°＋∠BOP，∴∠AOP＝∠BOP′.又∵OA＝OB，OP＝OP′，∴△AOP≌△BOP′.∴AP＝BP′.
(2)解：如图，连结OT，过点T作TH⊥OA于点H.
∵AT与eq \x\t(MN)相切，∴∠ATO＝90°.
∴AT＝eq \r(OA2－OT2)＝eq \r(102－62)＝8.
∵eq \f(1,2)OA·TH＝eq \f(1,2)AT·OT，即eq \f(1,2)×10×TH＝eq \f(1,2)×8×6，
∴TH＝eq \f(24,5)，即点T到OA的距离为eq \f(24,5).
(3)10°，170°.
16．如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O，使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系，并说明理由；
(2)若AC＝3，∠B＝30°.
①求⊙O的半径；
②设⊙O与AB边的另一个交点为E，求线段BD，BE
与劣弧DE所围成的阴影部分的面积(结果保留根号和π)．
解：(1)直线BC与⊙O相切．
理由如下：如图，连结OD，
∵OA＝OD，∴∠OAD＝∠ODA，
∵∠BAC的角平分线AD交BC边于点D，
∴∠CAD＝∠OAD，∴∠CAD＝∠ODA，∴OD∥AC，
∴∠ODB＝∠C＝90°，即OD⊥BC.
∴直线BC与⊙O相切．
(2)①设OA＝OD＝r，
∵在Rt△BDO中，∠B＝30°，∴OB＝2r，
∴在Rt△ACB中，∠B＝30°，∴AB＝2AC＝6，
∴3r＝6，解得r＝2.
②∵在Rt△ODB中，∠B＝30°，∴∠BOD＝60°，
∴S扇形ODE＝eq \f(60π×22,360)＝eq \f(2,3)π，
∴阴影部分面积为S△BOD－S扇形ODE＝2eq \r(3)－eq \f(2,3)π.