




《中考大一轮数学复习》课件 课时16 二次函数及其图像
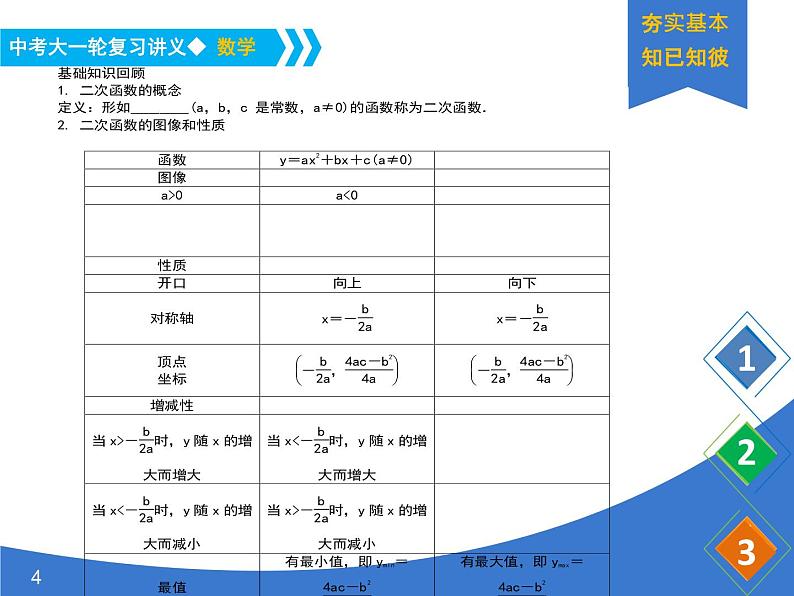
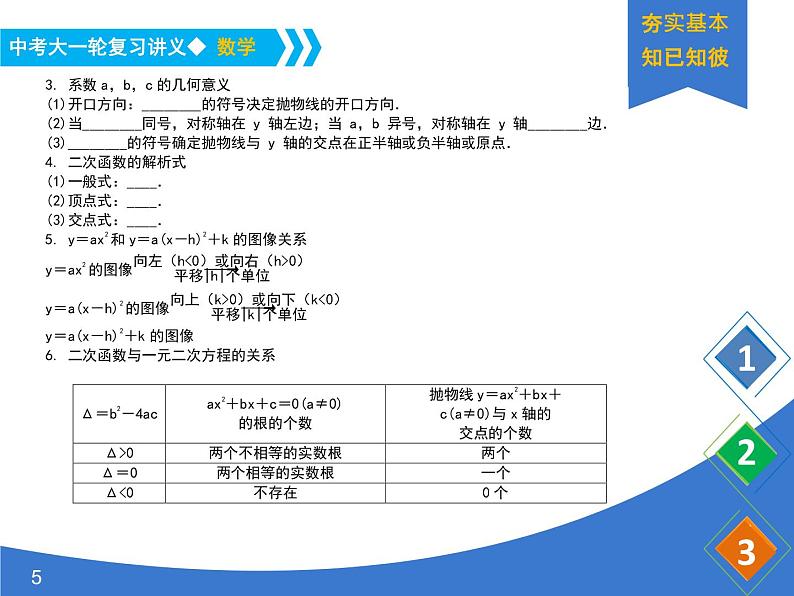
展开热点一 二次函数的图像与性质热点搜索 二次函数y=ax2+bx+c(a≠0)的图像位置、开口方向及大小等性质都与系数a,b,c有关系.具体如下:(1)a>0时开口向上; a<0时开口向下.(2)若a,b同号,则对称轴在y轴左侧;若a,b异号,则对称轴在y轴右侧;若b=0,则对称轴是y轴.(3)c>0时,抛物线与y轴的正半轴相交;c=0,抛物线过原点;c<0时,抛物线与y轴的负半轴相交.(4)b2-4ac>0时,抛物线与x轴有两个交点;b2-4ac<0时,抛物线与x轴没有交点;b2-4ac=0时,抛物线与x轴有一个交点.
典例分析1 (2013·四川资阳)如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,-2),且顶点在第三象限,设P=a-b+c,则P的取值范围是( )A. -4
典例分析2 (2013·四川雅安)将抛物线y=(x-1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )A. y=(x-2)2 B. y=(x-2)2+6C. y=x2+6 D. y=x2解析 抛物线y=(x-1)2+3向左平移1个单位,变为y=(x-1+1)2+3即y=x2+3;再向下平移3个单位后所得抛物线的解析式为y=x2+3-3即y=x2,故选D.
点对点训练3. (2014·江苏淮安)将二次函数y=2x2-1的图像沿y轴向上平移2个单位,则所得图像对应的函数表达式为________.4. (2012·宁波)把二次函数y=(x-1)2+2的图像绕原点旋转180°后得到的图像的解析式为________________.
y=-(x+1)2-2
热点三 二次函数的解析式热点搜索 求二次函数关系式通常有以下几种情形:(1)通过待定系数法求二次函数关系式:①已知图像上三点的坐标,用一般式y=ax2+bx+c(a≠0),②已知顶点坐标和任意一点坐标,用顶点式y=a(x-h)2+k(a≠0),③已知图像与x轴两个交点,用交点式y=a(x-x1)(x-x2)(a≠0).(2)通过平移、对称等变换求二次函数关系式.(3)利用变量之间的等量关系求实际问题中的函数关系式.典例分析3 (2013·北京)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.(1)求点A,B的坐标.(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式.(3)若该抛物线在-2
热点四 二次函数与一元二次方程热点搜索 求抛物线与坐标轴的交点坐标时,可转化为二次函数y=0或x=0,通过解方程解决交点的坐标问题.求抛物线与x轴的交点个数问题也可以转化为求一元二次方程根的情况.
解:因为y=-2x2-4x+1=-2(x+1)2+3,且-3≤x≤0,所以当x=-3时,函数y取得最小值y=-2×(-3)2-4×(-3)+1=-5;当x=-1时,函数y取得最大值为3.
《中考大一轮数学复习》课件 课时17 二次函数的应用: 这是一份《中考大一轮数学复习》课件 课时17 二次函数的应用,共22页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升等内容,欢迎下载使用。
《中考大一轮数学复习》课件 课时15 反比例函数及其图像: 这是一份《中考大一轮数学复习》课件 课时15 反比例函数及其图像,共18页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升等内容,欢迎下载使用。
《中考大一轮数学复习》课件 课时3 整式及其运算: 这是一份《中考大一轮数学复习》课件 课时3 整式及其运算,共19页。PPT课件主要包含了夯实基本知已知彼,知识结构梳理,课前预测你很棒,热点看台快速提升,055x,解-3,3n+1,n2+n+2等内容,欢迎下载使用。












