人教A版 (2019)必修 第一册1.3 集合的基本运算图片ppt课件

这是一份人教A版 (2019)必修 第一册1.3 集合的基本运算图片ppt课件，共24页。PPT课件主要包含了知识点1并集，A∪B，B∪A，B⊆A，知识点2交集，A∩B，B∩A，A⊆B，探究一并集运算，探究二交集运算等内容，欢迎下载使用。

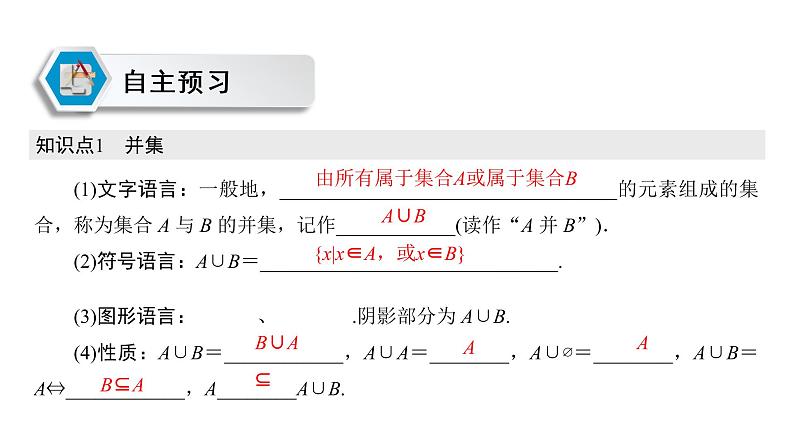
由所有属于集合A或属于集合B　
{x|x∈A，或x∈B}　
[微体验]1．集合A＝{1,2,3,4}，B＝{1,3,5,7}，则A∪B＝(　　)A．{1,3}　B．{1,2,3,4,5,7}C．{5,7}　D．{2,4,5,7}答案　B　解析　集合A与B所有的元素是1,2,3,4,5,7，A∪B＝{1,2,3,4,5,7}．
2．已知集合A＝{x|－1＜x＜2}，B＝{x|0＜x＜3}，则A∪B＝(　　)A．{x|－1＜x＜3}　B．{x|－1＜x＜0}C．{x|0＜x＜2}　D．{x|2＜x＜3}答案　A　解析　因为A＝{x|－1＜x＜2}，B＝{x|0＜x＜3}，所以A∪B＝{x|－1＜x＜3}．3．满足{1}∪B＝{1,2}的集合B的个数是______．解析　由{1}∪B＝{1,2}，故B＝{2}，{1,2}，共2个．答案　2
所有属于集合A且属于集合B的　
{x|x∈A，且x∈B}　
[微体验]1．若集合M＝{－1,1}，N＝{－2,1,0}，则M∩N＝(　　)A．{0，－1} 　B．{0} 　C．{1} 　D．{1,1}答案　C　解析　M∩N＝{－1,1}∩{－2,1,0}＝{1}．2．集合A＝{x|x＞0}，B＝{x|－1＜x≤3}，则A∩B＝(　　)A．{x|x＞0}　B．{x|x＞－1}C．{x|－1＜x≤3}　D．{x|0＜x≤3}答案　D　解析　A∩B就是找出两个集合的公共元素，由数轴得A∩B＝{x|0＜x≤3}．
3．集合M＝{(x，y)|y＝2x＋1}，N＝{y|y＝x－1}，则M∩N＝(　　)A．{－2}　B．{(－2，－3)}C．∅　D．{－3}答案　C　解析　集合M是点的集合，集合N是数的集合，两个集合没有公共元素，M∩N＝∅.
(1)设集合M＝{x|x2＋2x＝0，x∈R}，N＝{x|x2－2x＝0，x∈R}，则M∪N＝(　　)A．{0}　B．{0,2}C．{－2,0}　D．{－2,0,2}答案　D　解析　M＝{x|x2＋2x＝0，x∈R}＝{0，－2}，N＝{x|x2－2x＝0，x∈R}＝{0,2}，故M∪N＝{－2,0,2}．
(2)已知集合M＝{x|－3＜x≤5}，N＝{x|x＜－5或x＞5}，则M∪N＝(　　)A．{x|x＜－5或x＞－3}B．{x|－5＜x＜5}C．{x|－3＜x＜5}D．{x|x＜－3或x＞5}答案　A　解析　在数轴上表示集合M，N，如图所示，则M∪N＝{x|x＜－5或x＞－3}．
[方法总结]求集合并集的方法(1)两集合用列举法给出：①依定义，直接观察求并集；②借助Venn图写并集．(2)两集合用描述法给出：①直接观察，写出并集；②借助数轴，求出并集．(3)一个集合用描述法，另一个用列举法：①直接观察，找出并集；②借助图形，观察写出并集．提醒：若两个集合中有相同元素，在求其并集时只能算作一个．
[跟踪训练1]　(1)设S＝{x|x＜－1或x＞5}，T＝{x|a＜x＜a＋8}，若S∪T＝R，则实数a应满足(　　)A．－3＜a＜－1　B．－3≤a≤－1C．a≤－3或a＞－1　D．a＜－3或a＞－1答案　A　
(2)A＝{(x，y)|x＝2}，B＝{(x，y)|y＝2}．求A∪B，并说明其几何意义．解　A∪B＝{(x，y)|x＝2或y＝2}，其几何意义是直线x＝2和直线y＝2上所有的点组成的集合．
(1)(2018·全国卷Ⅰ)已知集合A＝{0,2}，B＝{－2，－1,0,1,2}，则A∩B＝(　　)A．{0,2}　B．{1,2}C．{0}　D．{－2，－1,0,1,2}答案　A　解析　A∩B＝{0,2}∩{－2，－1,0,1,2，}＝{0,2}．
(2)(2017·全国卷Ⅱ)设集合A＝{1,2,4}，B＝{x|x2－4x＋m＝0}．若A∩B＝{1}，则B＝(　　)A．{1，－3}　B．{1,0}C．{1,3}　D．{1,5}答案　C　解析　∵A∩B＝{1}，∴1∈B.∴1－4＋m＝0，即m＝3.∴B＝{x|x2－4x＋3＝0}＝{1,3}．(3)集合A＝{(x，y)|x＞0}，B＝{(x，y)|y＞0}，求A∩B并说明其几何意义．解　A∩B＝{(x，y)|x＞0且y＞0}，其几何意义为第一象限所有点的集合．
[方法总结]求集合交集的思路(1)识别集合：点集或数集．(2)化简集合：明确集合中的元素．(3)求交集：元素个数有限，利用定义或Venn图求解；连续数集，借助数轴求解．
[跟踪训练2]　(1)设集合A＝{x|－1≤x≤2}，B＝{x|0≤x≤4}，则A∩B等于(　　)A．{x|0≤x≤2}　B．{x|1≤x≤2}C．{x|0≤x≤4}　D．{x|1≤x≤4}答案　A　
(2)设集合A＝{x|－1≤x＜2}，B＝{x|x＜a}，若A∩B≠∅，则a的取值范围是(　　)A．a＜2　B．a＞－2C．a＞－1　D．－1＜a≤2答案　C　解析　在数轴上表示出集合A，B，由图可知．若A∩B≠∅，则a＞－1.
(3)A＝{－1,1,3}，B＝{a＋2，a2＋4}，A∩B＝{3}，则实数a＝________.解析　因为A∩B＝{3}，所以a＋2＝3或a2＋4＝3，且a＋2≠a2＋4.解得a＝1或a2＝－1(舍)．所以a＝1.答案　1
设集合A＝{－2}，B＝{x|ax＋1＝0，a∈R}．若A∩B＝B，求a的值．
探究三　并集、交集性质的应用
[跟踪训练3]　若集合A＝{x|－3≤x≤5}，B＝{x|2m－1≤x≤2m＋9}，A∪B＝B，求m的取值范围．
1．交集与并集的联系与区别联系：交集和并集都是由两个集合的元素组成的一个新的集合．区别：交集是由两个集合的所有公共元素组成的集合，而并集则是把两个集合的元素合并在一起，由合并后的所有元素所组成的集合．