

- 高考数学一轮复习第七章 7.5 试卷 试卷 0 次下载
- 高考数学一轮复习第七章 高考专题突破四 试卷 0 次下载
- 高考数学一轮复习第八章 8.1 试卷 试卷 0 次下载
- 高考数学一轮复习第八章 8.2 教案 教案 1 次下载
- 高考数学一轮复习第八章 8.3 试卷 试卷 1 次下载
高考数学一轮复习第七章 检测七
展开1.下列说法正确的是( )
A.空间中,两不重合的平面若有公共点,则这些点一定在一条直线上
B.空间中,三角形、四边形都一定是平面图形
C.空间中,正方体、长方体、四面体都是四棱柱
D.用一平面去截棱锥,底面与截面之间的部分所形成的多面体叫棱台
答案 A
解析 空间四边形不是平面图形,故B错;四面体不是四棱柱,故C错;平行于底面的平面去截棱台,底面和截面之间的部分所形成的多面体才叫棱台,故D错;根据公理2可知A正确,故选A.
2.(2020·南昌模拟)已知平面α内一条直线l及平面β,则“l⊥β”是“α⊥β”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
答案 B
解析 由题意,根据直线与平面垂直的判定定理,可得由“l⊥β,l⊂α”可证得“α⊥β”,即充分性是成立的;反之由“α⊥β,l⊂α”不一定得到“l⊥β”,即必要性不成立,所以“l⊥β”是“α⊥β”的充分不必要条件.
3.圆柱的底面积为S,侧面展开图是一个正方形,那么圆柱的侧面积是( )
A.4πS B.2πS
C.πS D.eq \f(2\r(3),3)πS
答案 A
解析 由πr2=S得圆柱的底面半径是eq \r(\f(S,π)),
故侧面展开图的边长为2π·eq \r(\f(S,π))=2eq \r(πS),所以圆柱的侧面积是4πS.
4.若平面α与β的法向量分别是a=(2,4,-3),b=(-1,2,2),则平面α与β的位置关系是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
答案 B
解析 因为a·b=(2,4,-3)·(-1,2,2)=0,所以a⊥b,所以平面α⊥β.
5.(2020·广州模拟)已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图所示),则四棱锥M-EFGH的体积为( )
A.eq \f(1,12) B.eq \f(1,4) C.eq \f(1,2) D.eq \f(1,3)
答案 A
解析 因为E,F,G,H分别为各个面的中心,显然E,F,G,H四点共面,截面如图所示.
显然四边形EFGH为正方形,且边长为eq \f(\r(2),2),
所以S正方形EFGH=eq \f(\r(2),2)×eq \f(\r(2),2)=eq \f(1,2).
另外易知点M到平面EFGH的距离为正方体棱长的一半,
即四棱锥M-EFGH的高为eq \f(1,2),
所以四棱锥M-EFGH的体积V=eq \f(1,3)×eq \f(1,2)×eq \f(1,2)=eq \f(1,12).
6.(2020·沈阳期末)在棱长为2的正方体ABCD-A1B1C1D1中,点P,Q,R分别为棱AA1,BC,C1D1的中点,经过P,Q,R三点的平面为α,平面α被此正方体所截得截面图形的面积为( )
A.3eq \r(3) B.6eq \r(2) C.eq \f(\r(3),2) D.eq \r(2)
答案 A
解析 如图所示,F,G,H是对应棱的中点.
易知,RF与HQ相交,确定一个平面.
HQ∥RG,故G在平面内,同理P在平面内.
故平面α被此正方体所截得截面图形为正六边形HPFQGR,边长为eq \r(2),
S=eq \f(1,2)×eq \r(2)×eq \r(2)sin eq \f(π,3)×6=3eq \r(3).
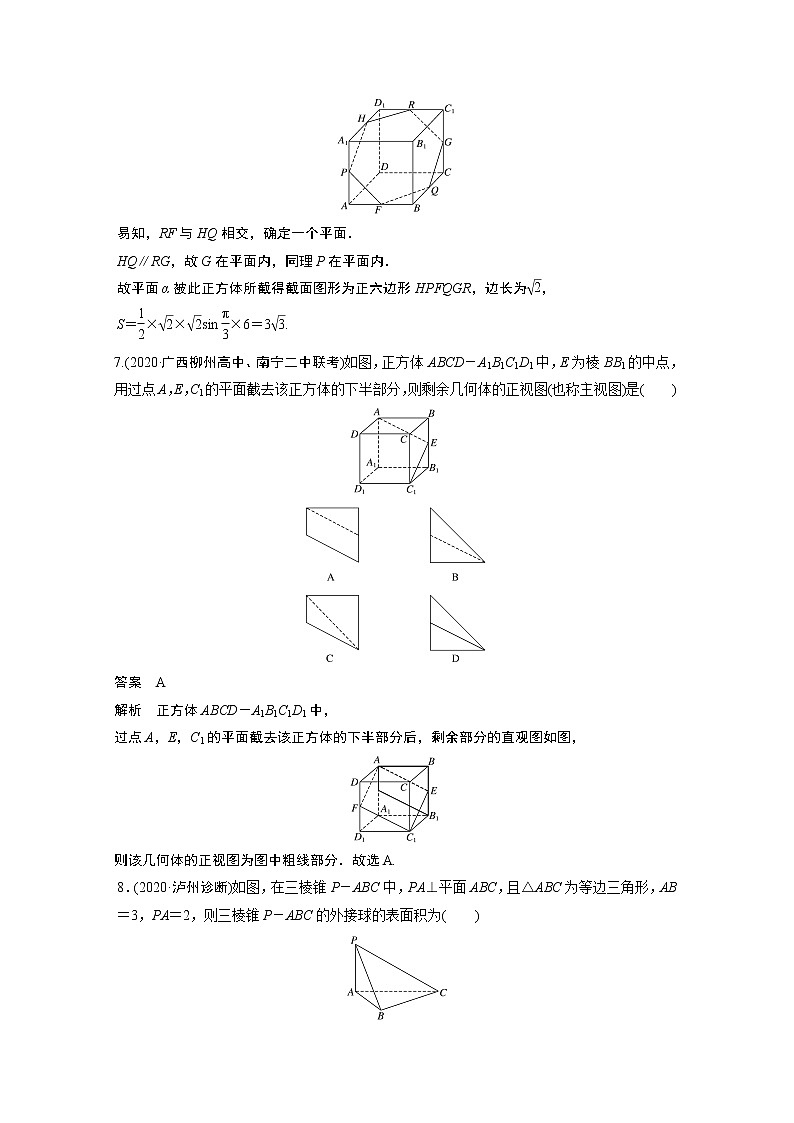
7.(2020·广西柳州高中、南宁二中联考)如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A,E,C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )
答案 A
解析 正方体ABCD-A1B1C1D1中,
过点A,E,C1的平面截去该正方体的下半部分后,剩余部分的直观图如图,
则该几何体的正视图为图中粗线部分.故选A.
8.(2020·泸州诊断)如图,在三棱锥P-ABC中,PA⊥平面ABC,且△ABC为等边三角形,AB=3,PA=2,则三棱锥P-ABC的外接球的表面积为( )
A.4π B.16π C.8π D.32π
答案 B
解析 由题意得三棱锥P-ABC的外接球球心在过△ABC的中心O1且垂直于平面ABC的直线上,设为点O,球半径设为R,则OO1=eq \f(PA,2)=1,AO1=eq \r(3),
∴R=eq \r(1+3)=2,从而外接球的表面积为4πR2=16π.
二、多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.在正方体ABCD-A1B1C1D1中,下列直线或平面与平面ACD1平行的有( )
A.直线A1B B.直线BB1
C.平面A1DC1 D.平面A1BC1
答案 AD
解析 对于A,由于A1B∥D1C,且A1B⊄平面ACD1,可得直线A1B∥平面ACD1;
对于B,由于B1B∥D1D,且D1D∩平面ACD1=D1,可得直线B1B不平行平面ACD1;
对于C,由于A1D与AD1相交,A1D⊂平面A1DC1,可得平面A1DC1不与平面ACD1平行;
对于D,由于C1B∥D1A,C1B⊄平面ACD1,所以C1B∥平面ACD1,又因为A1B∥平面ACD1,C1B∩A1B=B,所以平面A1BC1∥平面ACD1.
故选AD.
10.下列命题中不正确的是( )
A.若两条直线和同一个平面所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
D.若两个平面都垂直于第三个平面,则这两个平面平行
答案 ABD
解析 A项,若两条直线和同一个平面所成的角相等,则这两条直线平行、相交或异面,故A错误;
B项,若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行或相交,故B错误;
C项,设平面α∩β=a,l∥α,l∥β,由线面平行的性质定理知,在平面α内存在直线b∥l,在平面β内存在直线c∥l,所以由平行公理知b∥c,从而由线面平行的判定定理可证明b∥β,进而由线面平行的性质定理证明得b∥a,从而l∥a,故C正确;
D项,若两个平面都垂直于第三个平面,则这两个平面平行或相交,D错误.
故选ABD.
11.如图,已知棱长为1的正方体ABCD-A1B1C1D1中,下列命题正确的是( )
A.平面ACB1∥平面A1C1D,且两平面的距离为eq \f(\r(3),3)
B.点P在线段AB上运动,则四面体P-A1B1C1的体积不变
C.与所有12条棱都相切的球的体积为eq \f(\r(2)π,3)
D.M是正方体的内切球的球面上任意一点,N是△ACB1外接圆的圆周上任意一点,则|MN|的最小值是eq \f(\r(3)-\r(2),2)
答案 ABC
解析 A.∵AB1∥DC1,AC∥A1C1,且AC∩AB1=A,DC1∩A1C1=C1,
∴平面ACB1∥平面A1C1D,
长方体的体对角线BD1=eq \r(3),
设B到平面ACB1的距离为h,
则VB-AB1C=eq \f(1,3)×eq \f(1,2)×1×1×1
=eq \f(1,3)×eq \f(1,2)×eq \r(2)×eq \r(2)×eq \f(\r(3),2)h,即h=eq \f(\r(3),3),
则平面ACB1与平面A1C1D的距离d=eq \r(3)-2h=eq \r(3)-2×eq \f(\r(3),3)=eq \f(\r(3),3),故A正确,
B.点P在线段AB上运动,则四面体P-A1B1C1的高为1,底面积不变,则体积不变,故B正确,
C.与所有12条棱都相切的球的直径2R等于面的对角线B1C=eq \r(2),则2R=eq \r(2),R=eq \f(\r(2),2),
则球的体积V=eq \f(4,3)πR3=eq \f(4,3)×π×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))3=eq \f(\r(2)π,3),
故C正确,
D.设该正方体的内切球的球心为O,正方体的外接球的球心为O′,
则△ACB1的外接圆是正方体的外接球O′的一个小圆,
∵点M在正方体的内切球的球面上运动,点N在△ACB1的外接圆上运动,
∴线段MN长度的最小值是正方体的外接球的半径减去正方体的内切球的半径,
∵正方体ABCD-A1B1C1D1的棱长为1,
∴线段MN长度的最小值是eq \f(\r(3),2)-eq \f(1,2).故D错误,
故选ABC.
12.如图,已知在矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿线段DE翻折成△A1DE.若M为线段A1C的中点,则△ADE在翻折过程中,下列说法正确的是( )
A.线段BM的长是定值
B.存在某个位置,使DE⊥A1C
C.点M的运动轨迹是一个圆
D.存在某个位置,使MB⊥平面A1DE
答案 AC
解析 取CD的中点F,连接MF,BF,则MF∥DA1,BF∥DE,且MF∩BF=B,DA1∩DE=D,所以平面MBF∥平面A1DE,所以MB∥平面A1DE,D错误;由题意可知∠ADE=∠A1DE=∠MFB=eq \f(π,4),MF=eq \f(1,2)A1D,为定值,FB=DE,为定值,因此由余弦定理可得MB2=MF2+FB2-2MF·FB·cs∠MFB,所以MB是定值,所以点M在以B为圆心,BM为半径的圆上,故AC正确;由题意可知DE=CE=eq \r(2)AD=eq \f(\r(2),2)AB,则DE⊥CE,若B成立,且CE∩A1C=C,可得DE⊥平面A1EC,此时DE⊥A1E,与DA1⊥A1E矛盾,故B错误.综上可得AC正确,故选AC.
三、填空题(本大题共4小题,每小题5分,共20分)
13.把一个底面半径为3 cm,高为4 cm的钢质实心圆柱熔化,然后铸成一个实心钢球(不计损耗),则该钢球的半径为_____cm,表面积为_______cm2.(本题第一空2分,第二空3分)
答案 3 36π
解析 圆柱体积V圆柱=π×9×4=36π,球的体积V球=eq \f(4,3)πr3,
所以eq \f(4,3)πr3=36π,解得r=3,
所以球的表面积为4πr2=36π.
14.如图所示,在正三棱柱ABC-A1B1C1中,若各条棱长均为2,且M为A1C1的中点,则三棱锥M-AB1C的体积是________.
答案 eq \f(2\r(3),3)
解析 方法一 因为=---,
所以=2×eq \f(\r(3),4)×22-eq \f(1,3)×2×eq \f(1,2)×eq \f(\r(3),4)×22-eq \f(1,3)×2×eq \f(\r(3),4)×22-eq \f(1,3)×2×eq \f(1,2)×eq \f(\r(3),4)×22=eq \f(2\r(3),3).
方法二 ==eq \f(1,3)×S△AMC×h,
h是点B1到平面AMC的距离,
在正三棱柱ABC-A1B1C1中,M是A1C1的中点,
∴B1M⊥A1C1,且B1M⊥AA1,且A1C1∩AA1=A1,
∴B1M⊥平面ACC1A1,∴h=B1M=eq \r(3).
∴=eq \f(1,3)×eq \f(1,2)AC×AA1×B1M
=eq \f(1,6)×2×2×eq \r(3)=eq \f(2\r(3),3).
15.(2020·安顺联考)已知三棱锥P-ABC满足平面PAB⊥平面ABC,AC⊥BC,AB=4,∠APB=30°,则该三棱锥的外接球的表面积为__________.
答案 64π
解析 因为AC⊥BC,所以△ABC的外心为斜边AB的中点,
因为平面PAB⊥平面ABC,所以三棱锥P-ABC的外接球球心在平面PAB上,
即球心就是△PAB的外心,
根据正弦定理eq \f(AB,sin∠APB)=2R,解得R=4,
所以外接球的表面积为4πR2=64π.
16.(2020·武汉模拟)已知正方体ABCD-A′B′C′D′的棱长为3,垂直于棱AA′的截面分别与面对角线A′D,A′B,C′B,C′D相交于点E,F,G,H,则四棱锥A′-EFGH体积的最大值为________.
答案 eq \f(8,3)
解析 由题意得平面EFGH∥平面ABCD,
则EF∥BD∥HG,FG∥AC∥EH,
而AC⊥BD,所以EF⊥FG,
所以四边形EFGH为矩形,
易知△A′EF∽△A′BD,
设相似比为m,BD=eq \r(2)AB=3eq \r(2),
所以EF=3eq \r(2)m(0
而A′到平面EFGH的距离h=mAA′=3m,
所以四棱锥A′-EFGH的体积V=eq \f(1,3)Sh=eq \f(1,3)×18m(1-m)×3m=18(m2-m3),
V′=18(2m-3m2),
令V′=0得m=eq \f(2,3)或m=0(舍),
故当m∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(2,3)))时,V′>0,V在eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(2,3)))上单调递增,
当m∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3),+∞))时,V′<0,V在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3),+∞))上单调递减,
所以当m=eq \f(2,3)时,V取最大值,
Vmax=18×eq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)))2-\b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)))3))=eq \f(8,3).
四、解答题(本大题共6小题,共70分)
17.(10分)如图,在三棱柱ABC-A1B1C1中,AC=BC,E,F分别为AB,A1B1的中点.
(1)求证:AF∥平面B1CE;
(2)若A1B1⊥B1C,求证:平面B1CE⊥平面ABC.
证明 (1)在三棱柱ABC-A1B1C1中,AB∥A1B1 ,AB=A1B1,
∵E,F分别是AB,A1B1的中点,
∴FB1∥AB,FB1=eq \f(1,2)AB,AE=eq \f(1,2)AB,
∴FB1∥AE,FB1=AE,四边形FB1EA为平行四边形,
∴AF∥EB1.
又∵AF⊄平面B1CE,EB1⊂平面B1CE,
∴AF∥平面B1CE.
(2)由(1)知,AB∥A1B1,
∵A1B1⊥B1C,
∴AB⊥B1C,
又∵在△ABC中,AC=BC,E为AB的中点,
∴AB⊥EC.
又∵EC∩B1C=C,EC,B1C⊂平面B1CE,
∴AB⊥平面B1CE.
又∵AB⊂平面ABC,
∴平面ABC⊥平面B1CE.
18.(12分)(2020·日照期末)如图所示,在梯形CDEF中,四边形ABCD为正方形,且AE=BF=AB=1,将△ADE沿着线段AD折起,同时将△BCF沿着线段BC折起.使得E,F两点重合为点P.
(1)求证:平面PAB⊥平面ABCD;
(2)求点D到平面PBC的距离h.
(1)证明 ∵四边形ABCD为正方形,
∴AD⊥AB,
又∵AD⊥AE,即AD⊥PA,且PA∩AB=A,PA,AB⊂平面PAB,
∴AD⊥平面PAB,
又∵AD⊂平面ABCD,
∴平面PAB⊥平面ABCD.
(2)解 过点P作PO⊥AB交AB于O,如图所示,
由(1)知平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,
∴PO⊥平面ABCD,
∴VP-BCD=eq \f(1,3)×PO×S△BCD=eq \f(1,3)×eq \f(\r(3),2)×eq \f(1,2)=eq \f(\r(3),12),
又∵VP-BCD=VD-PBC,
∴eq \f(1,3)×S△PBC×h=eq \f(\r(3),12),
即eq \f(1,3)×eq \f(1,2)×1×1×h=eq \f(\r(3),12),
解得h=eq \f(\r(3),2),
∴点D到平面PBC的距离h=eq \f(\r(3),2).
19.(12分)(2020·株洲模拟)如图,已知三棱锥M-ABC中,MA=MB=MC=AC=2eq \r(2),AB=BC=2,O为AC的中点,点N在边BC上,且eq \(BN,\s\up6(→))=eq \f(2,3)eq \(BC,\s\up6(→)).
(1)证明:BO⊥平面AMC;
(2)求二面角N-AM-C的正弦值.
(1)证明 连接OM,
在△ABC中,AB=BC=2,AC=2eq \r(2),O为AC的中点,则OB⊥AC,且OB=eq \r(2).
在△MAC中,MA=MC=AC=2eq \r(2),O为AC的中点,则OM⊥AC,且OM=eq \r(6).
在△MOB中,满足BO2+OM2=MB2,
所以OB⊥OM,
又AC∩OM=O,AC,OM⊂平面AMC,
故OB⊥平面AMC.
(2)解 因为OB,OC,OM两两垂直,以O为坐标原点,建立如图所示的空间直角坐标系,
因为MA=MB=MC=AC=2eq \r(2),AB=BC=2,
则A(0,-eq \r(2),0),B(eq \r(2),0,0),C(0,eq \r(2),0),M(0,0,eq \r(6)),
eq \(AM,\s\up6(→))=(0,eq \r(2),eq \r(6)),eq \(BC,\s\up6(→))=(-eq \r(2),eq \r(2),0),
由eq \(BN,\s\up6(→))=eq \f(2,3)eq \(BC,\s\up6(→)),
所以Neq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),3),\f(2\r(2),3),0)),则eq \(AN,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),3),\f(5\r(2),3),0)),
设平面MAN的法向量为m=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(\(AN,\s\up6(→))·m=\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),3),\f(5\r(2),3),0))·x,y,z=\f(\r(2),3)x+\f(5\r(2),3)y=0,,\(AM,\s\up6(→))·m=0,\r(2),\r(6)·x,y,z=\r(2)y+\r(6)z=0,))
令y=eq \r(3),得m=(-5eq \r(3),eq \r(3),-1),
因为BO⊥平面AMC,
所以eq \(OB,\s\up6(→))=(eq \r(2),0,0)为平面AMC的法向量,
所以m=(-5eq \r(3),eq \r(3),-1)与eq \(OB,\s\up6(→))=(eq \r(2),0,0)所成角的余弦值为cs〈m,eq \(OB,\s\up6(→))〉=eq \f(-5\r(6),\r(79)×\r(2))=eq \f(-5\r(3),\r(79)).
所以二面角的正弦值为|sin〈m,eq \(OB,\s\up6(→))〉|=eq \r(1-\b\lc\(\rc\)(\a\vs4\al\c1(\f(-5\r(3),\r(79))))2)=eq \f(2,\r(79))=eq \f(2\r(79),79).
20.(12分)如图1,在平面四边形ABCD中,∠BAD=60°,AB=BD,BC⊥CD且BC=CD.将△CBD沿BD折成如图2所示的三棱锥C′-ABD,使二面角C′-BD-A的大小为30°.
(1)证明:AC′⊥BD;
(2)求直线BC′与平面C′AD所成角的正弦值.
(1)证明 在平面四边形ABCD中,∠BAD=60°,AB=BD,
所以△ABD为正三角形,
在三棱锥C′-ABD中,取BD的中点M,连接AM,C′M,
则AM⊥BD,C′M⊥BD,
因为AM∩C′M=M,AM,C′M⊂平面C′AM,
所以BD⊥平面C′AM,又AC′⊂平面C′AM,
所以AC′⊥BD.
(2)解 设AB=2,则AM=eq \r(3),C′M=1,
由(1)知,∠C′MA为二面角C′-BD-A的平面角,
所以∠C′MA=30°,
在△C′AM中,利用余弦定理可求得AC′=1,
所以△C′AM为等腰三角形,取AM的中点O,
则C′O⊥AM,又C′O⊥BD,AM∩BD=M,AM,BD⊂平面ABD,
所以C′O⊥平面ABD,取AB的中点N,则ON∥BD,且ON⊥AM,
所以以O为原点,建立如图所示的空间直角坐标系.
则Aeq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(\r(3),2),0)),Beq \b\lc\(\rc\)(\a\vs4\al\c1(1,\f(\r(3),2),0)),Deq \b\lc\(\rc\)(\a\vs4\al\c1(-1,\f(\r(3),2),0)),C′eq \b\lc\(\rc\)(\a\vs4\al\c1(0,0,\f(1,2))),
eq \(BC′,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-1,-\f(\r(3),2),\f(1,2))),eq \(AD,\s\up6(→))=(-1,eq \r(3),0),eq \(AC′,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(\r(3),2),\f(1,2))),
设平面C′AD的法向量为m=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(m·\(AD,\s\up6(→))=0,,m·\(AC′,\s\up6(→))=0,))
即eq \b\lc\{\rc\ (\a\vs4\al\c1(-x+\r(3)y=0,,\f(\r(3),2)y+\f(1,2)z=0,))
可取m=(eq \r(3),1,-eq \r(3)),
所以cs〈eq \(BC′,\s\up6(→)),m〉=eq \f(\(BC′,\s\up6(→))·m,|\(BC′,\s\up6(→))||m|)
=eq \f(-1×\r(3)-\f(\r(3),2)×1-\f(1,2)×\r(3),\r(1+\f(3,4)+\f(1,4))·\r(3+1+3))=-eq \f(\r(42),7).
所以直线BC′与平面C′AD所成角的正弦值为eq \f(\r(42),7).
21.(12分)(2020·宜昌模拟)如图所示,在三棱锥P-ABC中,PA⊥BC,AB=AP=1,BC=2eq \r(2),PC=eq \r(6),∠ABC=45°.
(1)求证:平面ABC⊥平面PAC;
(2)E为棱AC上一点,试确定点E的位置,使得直线PE与平面PBC所成角的正弦值为eq \f(\r(3),9).
(1)证明 在△ABC中,由余弦定理得AC2=BC2+AB2-2BC·AB·cs∠ABC
=(2eq \r(2))2+12-2×2eq \r(2)×1×cs 45°=5,
即AC=eq \r(5),
又PA=1,PC=eq \r(6),
∴PC2=PA2+AC2,∴PA⊥AC,
又PA⊥BC,AC∩BC=C,AC,BC⊂平面ABC,
∴PA⊥平面ABC,
又PA⊂平面PAC,
∴平面ABC⊥平面PAC.
(2)解 设BC的中点为D,连接AD,
∵BD=eq \f(1,2)BC=eq \r(2),AB=1,
又∠ABC=45°,∴AD⊥AB.
如图所示,以点A为坐标原点,以AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系.
则A(0,0,0),B(1,0,0),C(-1,2,0),P(0,0,1),
∴eq \(AC,\s\up6(→))=(-1,2,0),eq \(AP,\s\up6(→))=(0,0,1),eq \(BC,\s\up6(→))=(-2,2,0),eq \(BP,\s\up6(→))=(-1,0,1),
设eq \(AE,\s\up6(→))=λeq \(AC,\s\up6(→))=(-λ,2λ,0)(0≤λ≤1),
则eq \(PE,\s\up6(→))=eq \(AE,\s\up6(→))-eq \(AP,\s\up6(→))=(-λ,2λ,-1),
设平面PBC的法向量为n=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(BP,\s\up6(→))=0,,n·\(BC,\s\up6(→))=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(-x+z=0,,-2x+2y=0,))
令x=1,可得y=z=1,
∴n=(1,1,1),设直线PE与平面PBC所成的角为θ,
则sin θ=|cs〈n,eq \(PE,\s\up6(→))〉|=eq \f(|-λ+2λ-1|,\r(3)·\r(-λ2+2λ2+-12))
=eq \f(1-λ,\r(3)·\r(5λ2+1))=eq \f(\r(3),9),
整理得2λ2-9λ+4=0,
∵0≤λ≤1,∴λ=eq \f(1,2),∴E为棱AC的中点.
22.(12分)如图,已知长方形ABCD中,AB=2eq \r(2),AD=eq \r(2),M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E-AM-D的余弦值为eq \f(\r(5),5).
(1)证明 ∵长方形ABCD中,AB=2eq \r(2),AD=eq \r(2),M为DC的中点,
∴AM=BM=2,AB2=AM2+BM2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM⊂平面ABCM,
∴BM⊥平面ADM,
∵AD⊂平面ADM,
∴AD⊥BM.
(2)解 以AM的中点N为原点,建立如图所示的空间直角坐标系,
则M(-1,0,0),D(0,0,1),B(-1,2,0),A(1,0,0),
设eq \(DE,\s\up6(→))=λeq \(DB,\s\up6(→)),
则平面AMD的一个法向量为n=(0,1,0),
eq \(ME,\s\up6(→))=eq \(MD,\s\up6(→))+λeq \(DB,\s\up6(→))=(1-λ,2λ,1-λ),eq \(AM,\s\up6(→))=(-2,0,0),
设平面AME的一个法向量为m=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(\(AM,\s\up6(→))·m=0,,\(ME,\s\up6(→))·m=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(-2x=0,,x1-λ+2λy+1-λz=0,))
取y=1,得x=0,z=eq \f(2λ,λ-1),
所以m=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,1,\f(2λ,λ-1))),
因为cs〈m,n〉=eq \f(m·n,|m||n|)=eq \f(\r(5),5),解得λ=eq \f(1,2),
所以E为BD的中点时,二面角E-AM-D的余弦值为eq \f(\r(5),5).
2022届新高考一轮复习 第七章 数列 第2讲 等差数列及其前n项和 教案: 这是一份2022届新高考一轮复习 第七章 数列 第2讲 等差数列及其前n项和 教案,共23页。教案主要包含了变式1.1,变式1.2,变式1.3,变式2.1,变式3.1,变式4.1,变式4.2,变式5.1等内容,欢迎下载使用。
2022届新高考一轮复习 第七章 数列 第1讲 数列的概念与简单表示法 教案: 这是一份2022届新高考一轮复习 第七章 数列 第1讲 数列的概念与简单表示法 教案,共28页。教案主要包含了数列的有关概念,数列的表示方法,与的关系,数列的分类等内容,欢迎下载使用。
2022年新高考数学一轮复习考点练:5.5《单元检测》 (含答案详解)教案: 这是一份2022年新高考数学一轮复习考点练:5.5《单元检测》 (含答案详解)教案,共5页。












