高考数学一轮复习第七章 7.1

这是一份高考数学一轮复习第七章 7.1，共20页。试卷主要包含了1　空间几何体及其表面积、体积，旋转体的结构特征，三视图与直观图，多面体的表面积、侧面积，柱、锥、台、球的表面积和体积等内容，欢迎下载使用。

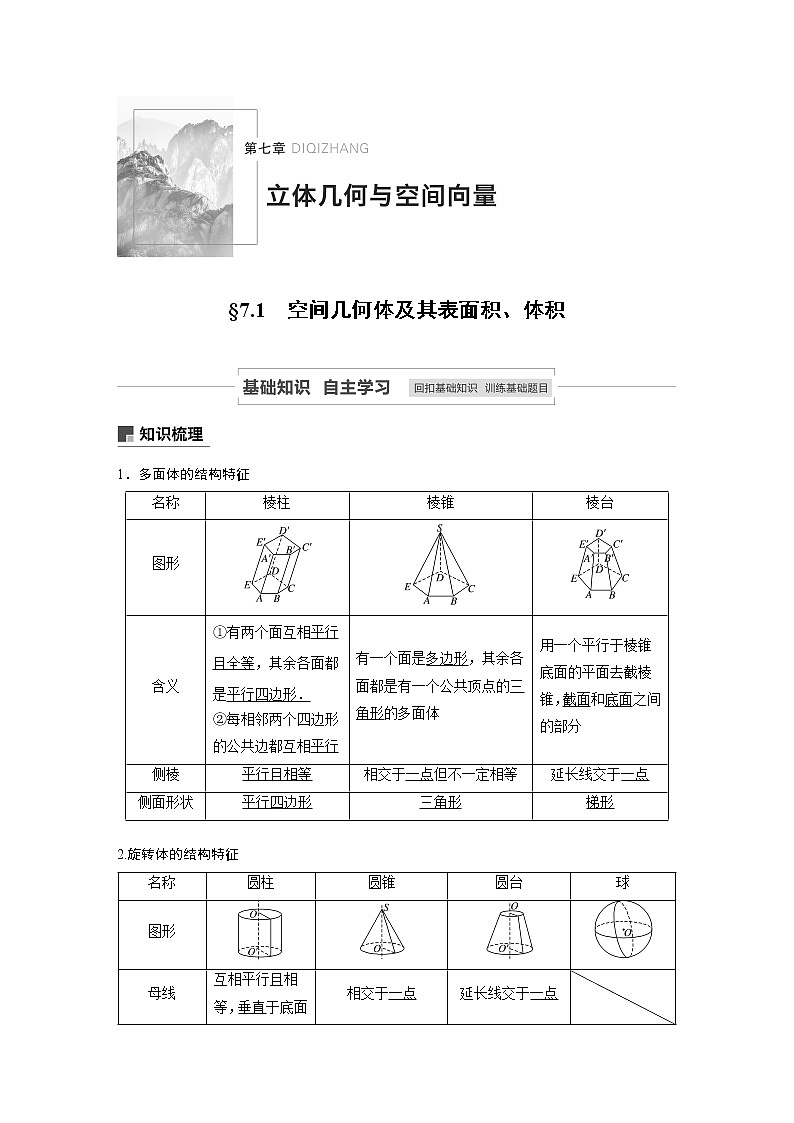
1．多面体的结构特征
2.旋转体的结构特征
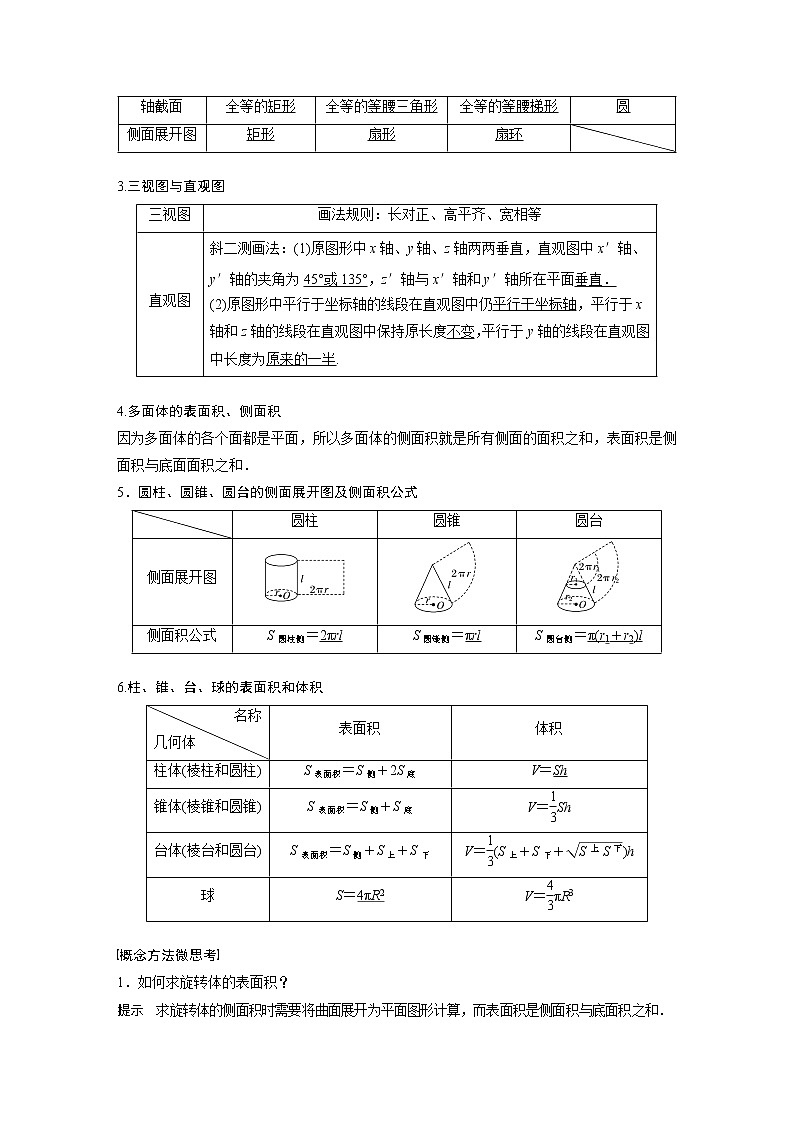
3.三视图与直观图
4.多面体的表面积、侧面积
因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．
5．圆柱、圆锥、圆台的侧面展开图及侧面积公式
6.柱、锥、台、球的表面积和体积
概念方法微思考
1．如何求旋转体的表面积？
提示 求旋转体的侧面积时需要将曲面展开为平面图形计算，而表面积是侧面积与底面积之和．
2．如何求不规则几何体的体积？
提示 求不规则几何体的体积要注意分割与补形，将不规则的几何体通过分割或补形转化为规则的几何体求解．
题组一 思考辨析
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)有一个面是多边形，其余各面都是三角形的几何体是棱锥．( × )
(2)正方体、球、圆锥各自的三视图中，三视图均相同．( × )
(3)台体的体积可转化为两个锥体的体积之差．( √ )
(4)锥体的体积等于底面积与高之积．( × )
题组二 教材改编
2．已知圆锥的表面积等于12π cm2，其侧面展开图是一个半圆，则底面圆的半径为( )
A．1 cm B．2 cm
C．3 cm D.eq \f(3,2) cm
答案 B
解析 S表＝πr2＋πrl＝πr2＋πr·2r＝3πr2＝12π，
∴r2＝4，∴r＝2.
3.如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________．
答案 1∶47
解析 设长方体的相邻三条棱长分别为a，b，c，它截出棱锥的体积V1＝eq \f(1,3)×eq \f(1,2)×eq \f(1,2)a×eq \f(1,2)b×eq \f(1,2)c＝eq \f(1,48)abc，剩下的几何体的体积V2＝abc－eq \f(1,48)abc＝eq \f(47,48)abc，所以V1∶V2＝1∶47.
题组三 易错自纠
4．体积为8的正方体的顶点都在同一球面上，则该球的表面积为( )
A．12π B.eq \f(32,3)π C．8π D．4π
答案 A
解析 由题意可知正方体的棱长为2，其体对角线长为2eq \r(3)即为球的直径，所以球的表面积为4πR2＝(2R)2π＝12π，故选A.
5．如图，直观图所表示的平面图形是( )
A．正三角形 B．锐角三角形
C．钝角三角形 D．直角三角形
答案 D
解析 由直观图中，A′C′∥y′轴，B′C′∥x′轴，还原后AC∥y轴，BC∥x轴．所以△ABC是直角三角形．故选D.
6．(2018·全国Ⅰ)某圆柱的高为2，底面周长为16，其三视图如图所示．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在侧视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为( )
A．2eq \r(17) B．2eq \r(5)
C．3 D．2
答案 B
解析 先画出圆柱的直观图，根据题中的三视图可知，点M，N的位置如图①所示．
圆柱的侧面展开图及M，N的位置(N为OP的四等分点)如图②所示，连接MN，则图中MN即为M到N的最短路径．
|ON|＝eq \f(1,4)×16＝4，|OM|＝2，
∴|MN|＝eq \r(|OM|2＋|ON|2)＝eq \r(22＋42)＝2eq \r(5).
故选B.
空间几何体
命题点1 三视图
例1 (2018·全国Ⅲ)中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是( )
答案 A
解析 由题意可知带卯眼的木构件的直观图如图所示，由直观图可知其俯视图应选A.
命题点2 直观图
例2 已知等腰梯形ABCD，上底CD＝1，腰AD＝CB＝eq \r(2)，下底AB＝3，以下底所在直线为x轴，则由斜二测画法画出的直观图A′B′C′D′的面积为________．
答案 eq \f(\r(2),2)
解析 如图所示，作出等腰梯形ABCD的直观图．
因为OE＝eq \r(\r(2)2－1)＝1，所以O′E′＝eq \f(1,2)，E′F＝eq \f(\r(2),4)，
则直观图A′B′C′D′的面积S′＝eq \f(1＋3,2)×eq \f(\r(2),4)＝eq \f(\r(2),2).
命题点3 展开图
例3 母线长为1的圆锥体，其侧面展开图的面积为eq \f(π,2)，则该圆锥的体积为________．
答案 eq \f(\r(3),24)π
解析 圆锥体其侧面展开图为扇形，S＝πrl＝eq \f(π,2)，解得r＝eq \f(1,2)，由圆锥的轴截面图可得h＝eq \f(\r(3),2)， V＝eq \f(1,3)πr2h＝eq \f(1,3)π×eq \f(1,4)×eq \f(\r(3),2)＝eq \f(\r(3),24)π.
思维升华 (1)由几何体求三视图，要注意观察的方向，掌握“长对正、高平齐，宽相等”的基本要求，由三视图推测几何体，可以先利用俯视图推测底面，然后结合正视图、侧视图推测几何体的可能形式．
(2)画几何体的直观图，掌握线段方向、长度两要素即可；几何体的展开图和原几何体的关系(形状和数量关系)是解题重点．
跟踪训练1 (1)如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )
A．三棱锥 B．三棱柱
C．四棱锥 D．四棱柱
答案 B
解析 由题意知，该几何体的三视图为一个三角形、两个四边形，经分析可知该几何体为三棱柱．
(2)如图，一个水平放置的平面图形的直观图(斜二测画法)是一个底角为45°、腰和上底长均为2的等腰梯形，则这个平面图形的面积是( )
A．2＋eq \r(2) B．1＋eq \r(2)
C．4＋2eq \r(2) D．8＋4eq \r(2)
答案 D
解析 由已知直观图根据斜二测画法规则画出原平面图形，如图所示，所以这个平面图形的面积为eq \f(4×2＋2＋2\r(2),2)＝8＋4eq \r(2)，故选D.
(3)(2019·北京市宣武区质检)将下面的展开图恢复成正方体后，∠ABC的度数为________．
答案 60°
解析 把图形复原后，连接三点恰好构成一个等边三角形，所以为60°.
表面积与体积
命题点1 表面积
例4 (1)(2018·全国Ⅰ)已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( )
A．12eq \r(2)π B．12π
C．8eq \r(2)π D．10π
答案 B
解析 设圆柱的轴截面的边长为x，
则由x2＝8，得x＝2eq \r(2)，
∴S圆柱表＝2S底＋S侧＝2×π×(eq \r(2))2＋2π×eq \r(2)×2eq \r(2)＝12π.故选B.
(2)(2019·淄博检测)某几何体的三视图如图所示，则该几何体的表面积为( )
A．3π＋4 B.eq \f(9,2)π＋4
C．4π＋2 D.eq \f(11,2)π＋4
答案 B
解析 由已知中的三视图可得该几何体是一个以俯视图为底面的四分之三圆柱，其底面半径为1，高为2，
故其表面积S＝2×eq \f(3,4)×π×12＋eq \f(3,4)×2π×1×2＋2×2×1＝eq \f(9π,2)＋4.故选B.
命题点2 体积
例5 (1)如图，正三棱柱ABC－A1B1C1的底面边长为2，侧棱长为eq \r(3)，D为BC的中点，则三棱锥A－B1DC1的体积为( )
A．3 B.eq \f(3,2)
C．1 D.eq \f(\r(3),2)
答案 C
解析 如题图，因为△ABC是正三角形，
且D为BC中点，则AD⊥BC.
又因为BB1⊥平面ABC，AD⊂平面ABC，
故BB1⊥AD，且BB1∩BC＝B，BB1，BC⊂平面BCC1B1，
所以AD⊥平面BCC1B1，
所以AD是三棱锥A－B1DC1的高．
所以＝eq \f(1,3) ·AD
＝eq \f(1,3)×eq \r(3)×eq \r(3)＝1.
(2)(2017·全国Ⅱ)如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为( )
A．90π B．63π
C．42π D．36π
答案 B
解析 方法一 (割补法)由几何体的三视图可知，该几何体是一个圆柱截去上面虚线部分所得，如图所示．
将圆柱补全，并将圆柱从点A处水平分成上下两部分．由图可知，该几何体的体积等于下部分圆柱的体积加上上部分圆柱体积的eq \f(1,2)，所以该几何体的体积V＝π×32×4＋π×32×6×eq \f(1,2)＝63π.故选B.
方法二 (估值法)由题意知，eq \f(1,2)V圆柱