2021学年3.4 函数的应用（一）教学演示课件ppt

这是一份2021学年3.4 函数的应用（一）教学演示课件ppt，共22页。PPT课件主要包含了探究一分段函数模型，探究二二次函数模型等内容，欢迎下载使用。
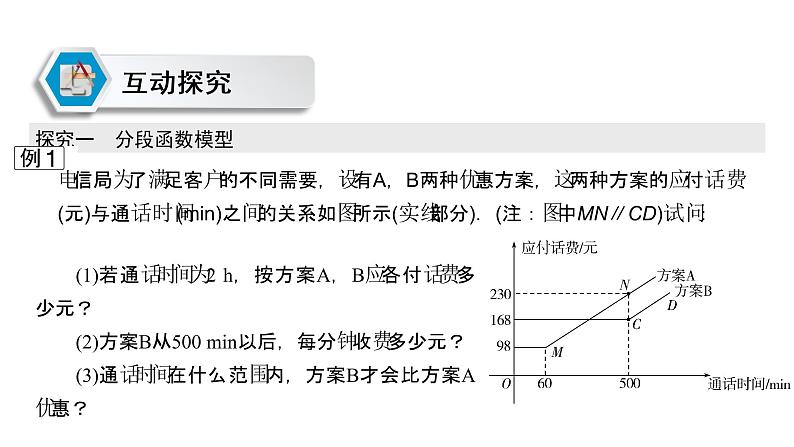
电信局为了满足客户的不同需要，设有A，B两种优惠方案，这两种方案的应付话费(元)与通话时间(min)之间的关系如图所示(实线部分)．(注：图中MN∥CD)试问：
(1)若通话时间为2 h，按方案A，B应各付话费多少元？(2)方案B从500 min以后，每分钟收费多少元？(3)通话时间在什么范围内，方案B才会比方案A优惠？
[方法总结]1．一次函数模型的特点和求解方法(1)一次函数模型的突出特点是其图象是一条直线．(2)解一次函数模型时，注意待定系数法的应用，主要步骤是：设元、列式、求解．2．分段函数模型应用的两个注意点(1)分段对待：分段函数主要是每一段自变量变化所遵循的规律不同，可以先将其当成几个问题，将各段的变化规律分别找出来，再将其合到一起，要注意各段自变量的取值范围，特别是端点值．(2)原则：构造分段函数时，要力求准确、简洁，做到分段合理、不重不漏．
[跟踪训练1]　为方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示：(1)分别求出通话费y1，y2与通话时间x之间的函数解析式；(2)请帮助用户计算，在一个月内使用哪种卡更便宜．
牧场中羊群的最大蓄养量为m只，为保证羊群的生长空间，实际蓄养量不能达到最大蓄养量，必须留出适当的空闲率．已知羊群的年增长量y只和实际蓄养量x只与空闲率的乘积成正比，比例系数为k(k>0)．(1)写出y关于x的函数关系式，并指出这个函数的定义域；(2)求羊群年增长量的最大值；(3)当羊群的年增长量达到最大值时，求k的取值范围．
[变式探究]　若将本例“与空闲率的乘积成正比”改为“与空闲率的乘积成反比”，又如何表示出y关于x的函数关系式？
[方法总结]利用二次函数求最值的方法及注意点方法：根据实际问题建立函数模型解析式后，可利用配方法、判别式法、换元法利用函数的单调性等方法求最值，从而解决实际问题中的利润最大、用料最省等最值问题．注意点：取得最值时的自变量与实际意义是否相符.
[跟踪训练2]　据市场分析，某海鲜加工公司，当月产量在10吨至25吨时，月生产总成本y(万元)可以看成月产量x(吨)的二次函数；当月产量为10吨时，月总成本为20万元；当月产量为15吨时，月总成本最低为17.5万元，为二次函数的顶点．(1)写出月总成本y(万元)关于月产量x(吨)的函数关系式；(2)已知该产品销售价为每吨1.6万元，那么月产量为多少时，可获得最大利润．
某药厂研制出一种新型药剂，投放市场后其广告投入x(万元)与药品利润y(万元)存在的关系为y＝xα(α为常数)，其中x不超过5万元，已知去年投入广告费用为3万元时，药品利润为27万元，若今年广告费用投入5万元，预计今年药品利润为________万元．解析　由已知投入广告费用为3万元时，药品利润为27万元，代入y＝ xα中，即3α＝27，解得α＝3，故函数解析式为y＝x3，所以当x＝5时，y＝125.答案　125
探究三　幂函数模型应用举例
[方法总结]处理幂函数模型的步骤(1)阅读理解、认真审题．(2)用数学符号表示相关量，列出函数解析式．(3)根据幂函数的性质推导运算，求得结果．(4)转化成具体问题，给出解答．
[跟踪训练3]　某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0.125万元和0.5万元．(1)分别写出两类产品的收益与投资额的函数关系；(2)该家庭有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？