初中数学人教版八年级下册18.1.2 平行四边形的判定教学ppt课件

这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定教学ppt课件，共27页。PPT课件主要包含了数学语言，学习目标，∴∠B∠D，平行四边形的判定，判定3，C2233，∠240〫，∵AEBC，课后作业等内容，欢迎下载使用。

平行四边形的判定1（定义法）： 两组对边分别平行的四边 形是平行四边形.
∵ AB//CD、AD//BC∴四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形.
数学语言：∵ AB=CD、AD=BC∴四边形ABCD是平行四边形
探索并证明平行四边形的判定定理.能熟练运用平行四边形的判定定理去计算 和证明.
思考 请写出平行四边形对角相等的逆命题.
如果一个四边形是平行四边形，那么它的两组对角相等.如果一个四边形的两组对角分别相等，那么这个四边形 是平行四边形.这个逆命题是真命题吗？
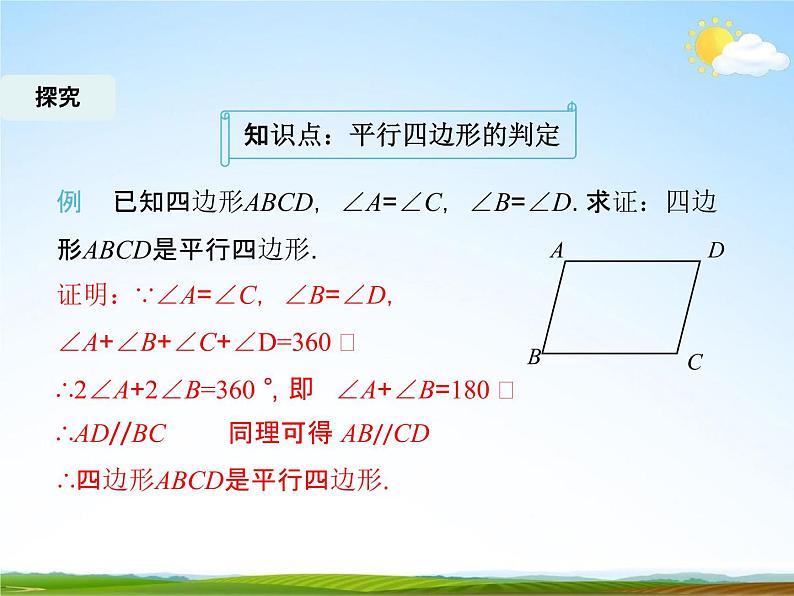
知识点：平行四边形的判定
例已知四边形ABCD，∠A=∠C，∠B=∠D. 求证：四边
形ABCD是平行四边形.证明：∵∠A=∠C，∠B=∠D，
∠A+∠B+∠C+∠D=360 〫
∴四边形ABCD是平行四边形.
∴2∠A+2∠B=360 〫，即∠A+∠B=180 〫∴AD//BC同理可得 AB//CD
平行四边形的判定3： 两组对角分别相等的四边形是平 行四边形.
数学语言：∵ ∠A=∠C，∠B=∠D∴四边形ABCD是平行四边形
通过以上例题，你能总结出什么 判定方法呢？
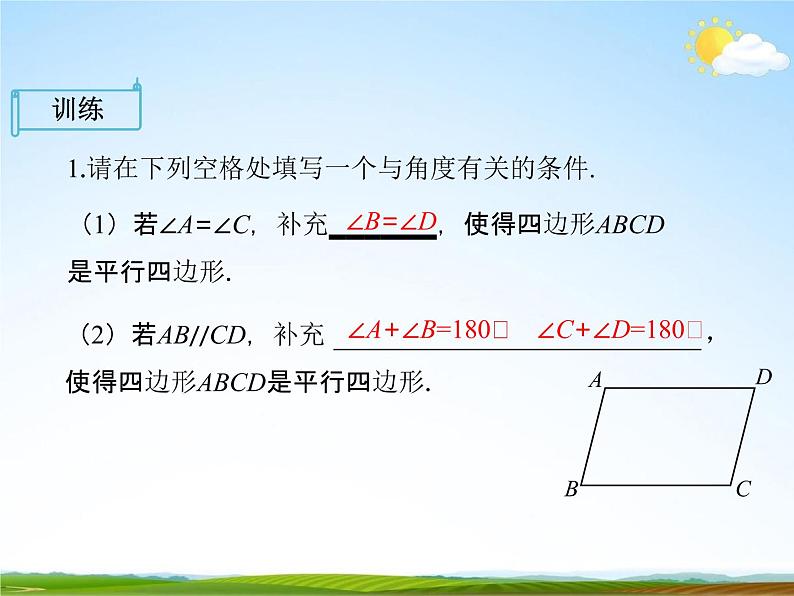
1.请在下列空格处填写一个与角度有关的条件.
（2）若AB//CD，补充
使得四边形ABCD是平行四边形.
（1）若∠A=∠C，补充 ∠B=∠D ，使得四边形ABCD 是平行四边形.
∠A+∠B=180〫或∠C+∠D=180〫，
2. 下列条件中，不能判定四边形ABCD是平行四边形的是
（A）.A. ∠A+∠B=180〫,∠C+∠D=180〫B. ∠A=∠B=∠C=∠D=90〫C. ∠A=∠C，∠B=∠DD. ∠A+∠B=180〫,∠B+∠C=180〫
1.一个四边形ABCD 的三个内角∠A 、∠B 、∠C 的度数
依次如下，其中可以判定是平行四边形的是（）.
A. 80 〫，100 〫，100 〫C. 40 〫，40 〫，140 〫
B. 40 〫，140 〫，40 〫D. 80 〫，80 〫，100 〫
A．5种B．4种C．3种
解：当D①．③1时种，四边形ABCD为平行四边形； A当①④时，四边形ABCD为平行四边形；
当③④时，四边形ABCD为平行四边形.
2.顺次连接平面上A，B，C，D四点得到一个四边形，从①AB∥CD，②BC＝AD，③∠A＝∠C，④∠B＝∠D四个 条件中任取两个，可以得出“四边形ABCD是平行四边形” 这一结论的情况共有(C)
3.如图，已知在平行四边形ABCD中，AE、CF分别是∠DAB、∠BCD的角平分线. 求证：四边形AFCE是平行四边 形.
解析：利用平行四边形的性质和角 平分线的性质，找到相等的角和相 等的边.通过“两组对角分别相等” 来证明该四边形是平行四边形.
证明： ∵ AE、CF分别是∠DAB、∠BCD的角平分线
∴∠DAE=∠BAE，∠DCF=∠BCF∵四边形ABCD是平行四边形∴∠DAB=∠BCD，则∠DCF=∠BCF=∠BAE=∠DAE
∵四边形ABCD是平行四边形
∵ 在△ABE 和△CDF中，
∵ ∠ECF=∠FAE，∠AFC=∠CEA∴四边形AFCE是平行四边形
∠B=∠D， ∠BAE=∠DCF∠DFC=180〫-∠DCF-∠D，∠BEA=180〫-∠BAE-∠BD∴∠DFC=∠BEA，则∠AFC=∠CEA
两组对角分别相等的四边形 是平行四边形.
∵ ∠A=∠C，∠B=∠D∴四边形ABCD是平行四边形
1.四边形ABCD中，∠A、∠B、∠C、∠D的度数之比如下，
能判定四边形ABCD是平行四边形的是（）.
A. 1：2：3：4B. 2：3：2：3
D. 1：2：3：3A
设单位度数为 x .A. x+2x+3x+4x=360〫，解得：x=36〫，度数为36〫、72〫、108〫、144〫.B. 2x+3x+2x+3x=360〫，解得：x=36〫，度数为72〫、 108〫、72〫、108〫.
设单位度数为 x .C. 2x+2x+3x+3x=360〫，解得：x=36〫，度数为36〫、 36〫、108〫、108〫.D. x+2x+3x+3x=360〫，解得：x=40〫，度数为40〫、80〫、120〫、120〫.
2.如图，在四边形ABCD中，AB//CD，∠C=55〫，∠1=85〫，
求∠A的度数；求证：四边形ABCD是平行四边形.
解：（1）∵∠A+∠1+∠2=180°∴∠A=180°-∠1-∠2=180°-85°-40°=55°
（2）证明：∵AB//DC
∴四边形ABCD是平行四边形
∴∠ABC+∠C=180°，∠ADC+∠A=180°，∵∠A=∠C=55°∴∠ABC=∠ADC
3.如图，E是ABCD 的边 AD 延长线上一点，连接BE、CE、
BD、BE 交 CD 于点 F. 添加以下条件，不能判定四边形BCED
为平行四边形的是（）.
A.∠ABD=∠DCEC.∠AEB=∠BCD
B.DF=CFD.∠AEC=∠CBD
A.∠ABD=∠DCE正确
∵四边形ABCD是平行四边形∴ AB//DC，AD//BC∴ DE//BC，∠ABD=∠CDB∵∠ABD=∠DCE∴∠CDB=∠DCE∴ BD//CE，四边形BCED是平行四边形
确∵DE//BC∴∠DEF=∠CBF
在△DEF 和△CBF 中， ∵∠DEF=∠CBF，∠DFE=∠CFB，DF=CF∴ △DEF≌△CBF∴ EF=BF∵DF=CF
∴四边形BCED是平行四边形
C.∠AEB=∠BCD错误
∴ 不能判定四边形BCED是平行四边形
∴ ∠AEB=∠CBF∵∠AEB=∠BCD∴∠CBF=∠BCD∴ CF=BF，同理EF=DF
∴ ∠DEC+∠BCE= ∠EDB+∠DBC=180〫∵∠AEC=∠CBD∴∠BDE=∠BCE∴ 四边形BCED是平行四边形
D. ∠AEC=∠CBD正确
请完成课本后习题第9题。