




数学18.1.1 平行四边形的性质教学课件ppt
展开掌握平行四边形的概念.探索并熟练运用平行四边形的性质.
这些生活中常见的平行四边形,你有注意到吗?
知识点1:平行四边形的概念
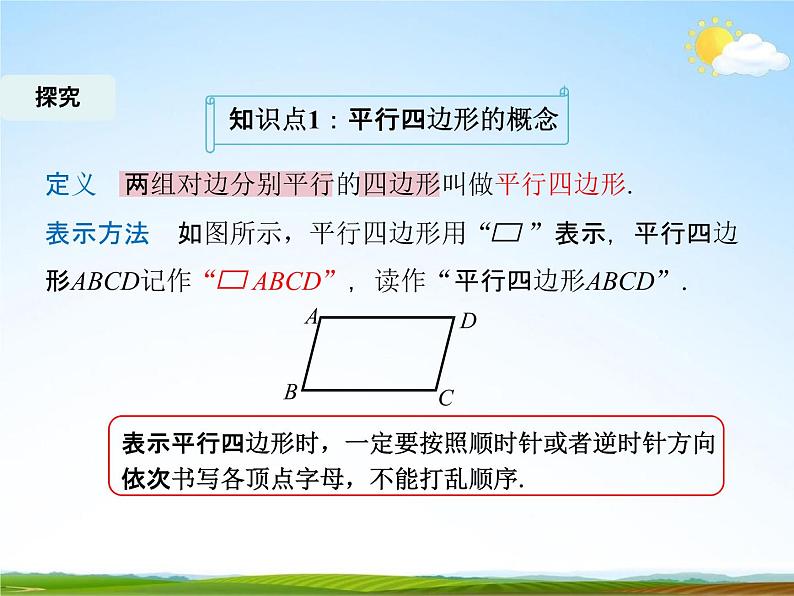
定义两组对边分别平行的四边形叫做平行四边形.表示方法如图所示,平行四边形用“”表示,平行四边 形ABCD记作“ABCD”,读作“平行四边形ABCD”.
表示平行四边形时,一定要按照顺时针或者逆时针方向 依次书写各顶点字母,不能打乱顺序.
平行四边形的定义既是性质,又是判定:由定义可知平 行四边形的两组对边分别平行;由定义可以得到只要四边形 中的两组对边分别平行,那么这个四边形就是平行四边形.
∵ 四边形ABCD是平行四边形∴AB∥C ADD∥BC
∵ AB∥CD AD∥BC∴ 四边形ABCD是平行四边形
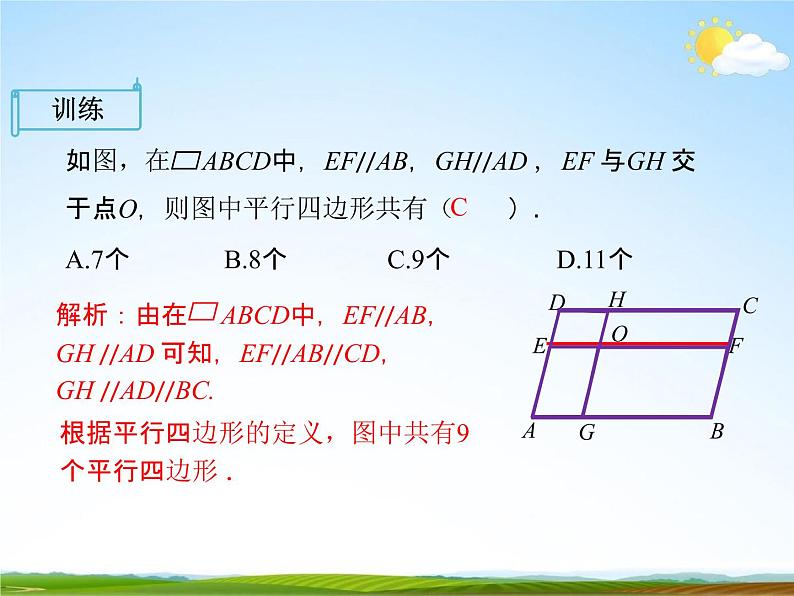
如图,在ABCD中,EF//AB,GH//AD ,EF 与GH 交 于点O,则图中平行四边形共有(C).
A.7个B.8个C.9个D.11个解析:由在ABCD中,EF//AB,
GH //AD 可知,EF//AB//CD,GH //AD//BC.根据平行四边形的定义,图中共有9 个平行四边形 .
知识点2:平行四边形的性质
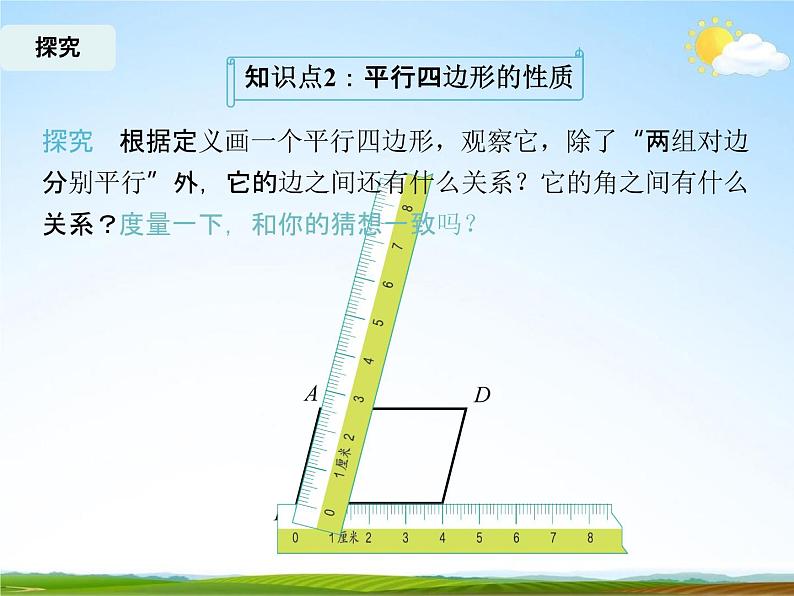
探究 根据定义画一个平行四边形,观察它,除了“两组对边 分别平行”外,它的边之间还有什么关系?它的角之间有什么 关系?度量一下,和你的猜想一致吗?
猜想:对边相 等,对角相等.
如图,已知平行四边形ABCD,其中AB // CD,AD // BC,
求证: AB=CD,AD = BC,∠ABC= ∠ADC,∠BAD= ∠BCD.
分析:构造三角形,利用全等三角形 的性质来得到对应边相等,对应角相
等.在平行四边形中,连接任意一条对 角线即可分成两个三角形.
证明:如图所示,连接AC.
∵ AB // CD,AD // BC∴ ∠1=∠4, ∠2=∠3.A
又 AC是△ABC 和△CDA的公共边,∴△ABC≌△CDA.∴AB=CD, AD=BC, ∠B= ∠D.∵ ∠BAD= ∠1+∠2, ∠BCD = ∠3+∠4,∴ ∠BAD= ∠BCD.
性质1平行四边形的对边相等.
数学语言∵四边形ABCD是平行四边形∴AD=BC,AB=CD.
性质2平行四边形的对角相等.数学语言∵四边形ABCD是平行四边形,∴ ∠A= ∠C , ∠B= ∠D.
例1如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为 E,F. 求证:AE=CF.证明: ∵四边形ABCD 是平行四边形∴ ∠A= ∠C , AD=CB∵ DE⊥AB,BF⊥CD∴ ∠AED=∠CFB=90〫∵ 在△ADE和△CBF中, ∠A= ∠C ,∠AED=∠CFB,AD=CB.∴△ADE≌△CBF (AAS),∴ AE=CF.
ABCD中,连接AC、BD,并设它
们相交于点 O,OA与OC,OB与OD有什么关系?A猜想:在ABCD中, OA=OC,OB=OD
ABCD中,对角线AC、BD相交于点O. 求证:
OA=OC,OB=OD .证明: ∵四边形ABCD 是平行四边形∴ AD//CB, AD=CB
∵ AD//CB∴∠DAO=∠BCO, ∠ADO=∠CBO∵ 在△ADO 和△CBO 中, ∠DAO=∠BCO,AD=CB∠ADO=∠CBO∴ △ADO ≌△CBO (ASA), OA=OC,OB=OD.
性质3平行四边形的对角线互相平分.
ABCD中,AB=10,AD=8,AC⊥BC.求BC、
CD、AC、OA的长,以及
解: ∵四边形ABCD 是平行四边形∴ BC=AD=8,CD=AB=10∵ AC⊥BC∴△ABC是直角三角形
训练如图,在ABCD 中,已知 AD=5,CD=7,求它的周长.
解: ∵四边形ABCD 是平行四边形∴ AD=BC,AB=CD∵ AD=5,CD=7∴ BC=5,AB=7
∴ABCD的周长为AB+BC+CD+AD=24.
1.如图,在ABCD中,E,F是直线BD上的两点,且DE=BF,
求证:AE=CF.证明: ∵四边形ABCD 是平行四边∴形∠ADB= ∠CBD , AD=CB∵ E,F是直线BD上的两点
∴ ∠ADE=180〫-∠ADB,∠CBF=180〫-∠CBD, ∴∠ADE= ∠CBF∵ 在△ADE和△CBF中,DE=BF,∠ADE=∠CBF,AD=CB.∴△ADE≌△CBF (SAS), AE=CF.
ABCD中,∠A=38〫,求其余各内角的度
解: ∵在ABCD中,∠A=38〫∴∠C=∠A=38〫∵ AD//CB∴∠B=∠D=180〫-38〫=142〫∴∠B、 ∠C 、∠D的度数分别为142〫、 38〫、 142〫.
3.ABCD的对角线AC、BD相交于点O,EF过点O且
与AB、CD分别相交于点E、F.求证:OE=OF.
证明: ∵四边形ABCD 是平行四边形∴ OA=OC, AB//CD∴∠EAO=∠FCO
∵ 在△AOE和△COF中, ∠EAO=∠FCO ,OA=OC,∠AOE=∠COF.∴△ADE≌△CBF (ASA), OE=OF.
两组对边分别平行的四边 形叫做平行四边形.
①对边相等②对角相等③对角线互相平分
1. 在ABCD中,对角线AC、BD交于点O,下列式子中不一定
成立的是(). A . AB//CD
C. ∠ABC+∠BCD=180〫
B. OA=OCD. AB=BCD
2.在ABCD中,E、F是AC上的两点,AE=CF,求证:
BE=DF.证明: ∵在ABCD中,AB//CD∴∠BAE=∠DCF∵在△ABE 和△CDF中,AB=CD,∠BAE=∠DCF, AE=CF∴△ABE≌△CDF(SAS), BE=DF
∵ AC⊥BC, AB=10
3. 在ABCD中,AB=10, AD=6,AC⊥BC,则 BD 的长 为多少?
请完成课本后习题第1题。
初中数学人教版八年级下册18.2.3 正方形教学课件ppt: 这是一份初中数学人教版八年级下册18.2.3 正方形教学课件ppt,共31页。PPT课件主要包含了有一个直角,课后作业等内容,欢迎下载使用。
人教版八年级下册18.1.1 平行四边形的性质教学课件ppt: 这是一份人教版八年级下册18.1.1 平行四边形的性质教学课件ppt,共28页。PPT课件主要包含了数学语言,学习目标,通过测量ACBD,bBC,GED,两条平行线之间的距离,aAD,课后作业等内容,欢迎下载使用。
初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理教学课件ppt: 这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理教学课件ppt,共33页。PPT课件主要包含了直角三角形,学习目标,abc,cba,abcc,a勾C,勾股定理,刘徽“青朱出入图”,课后作业等内容,欢迎下载使用。













