人教版八年级下册19.2 一次函数综合与测试教学课件ppt

这是一份人教版八年级下册19.2 一次函数综合与测试教学课件ppt，共28页。PPT课件主要包含了知识梳理，二元一次方程，二元一次方程组，从“数”上看，从“形”上看，2二元一次方程组，重点解析，的交点坐标是，A05，B0-5等内容，欢迎下载使用。

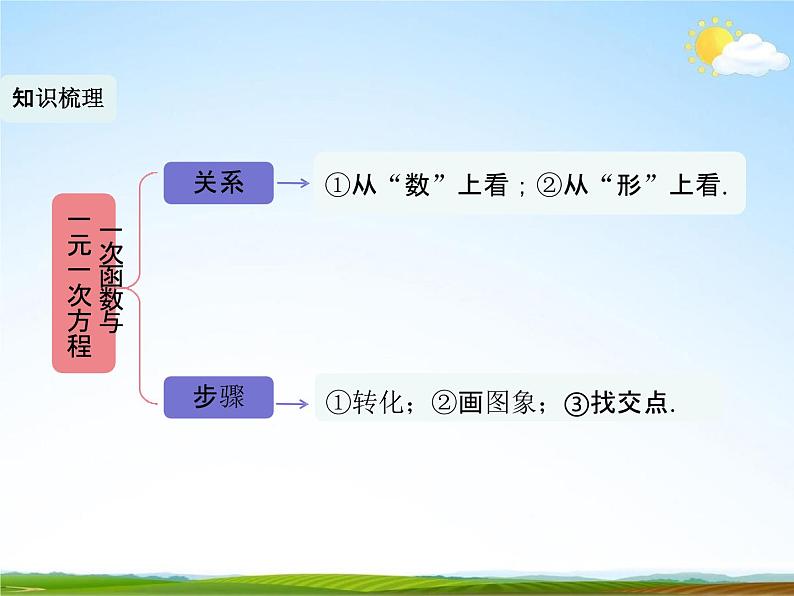
一次函数与一元一次方程
①从“数”上看；②从“形”上看.
①转化；②画图象；③找交点.
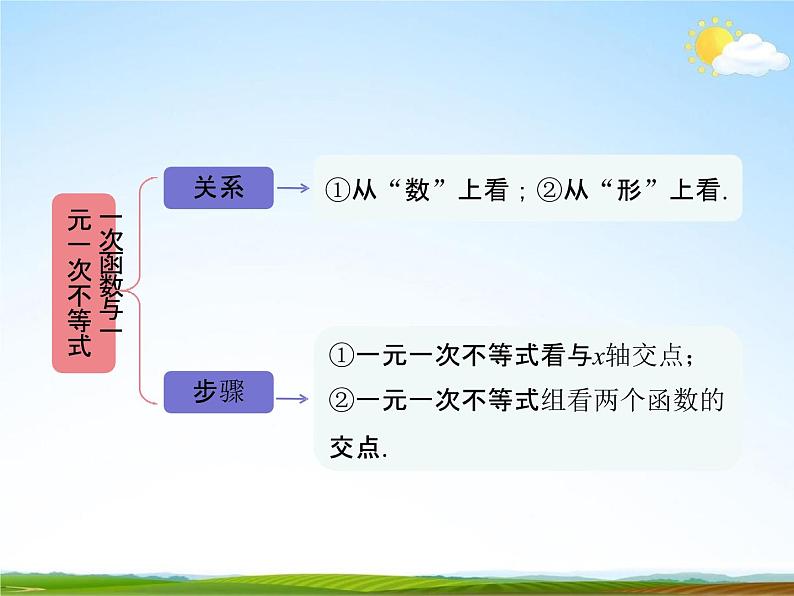
一次函数与一元一次不等式
①一元一次不等式看与x轴交点；②一元一次不等式组看两个函数的 交点.
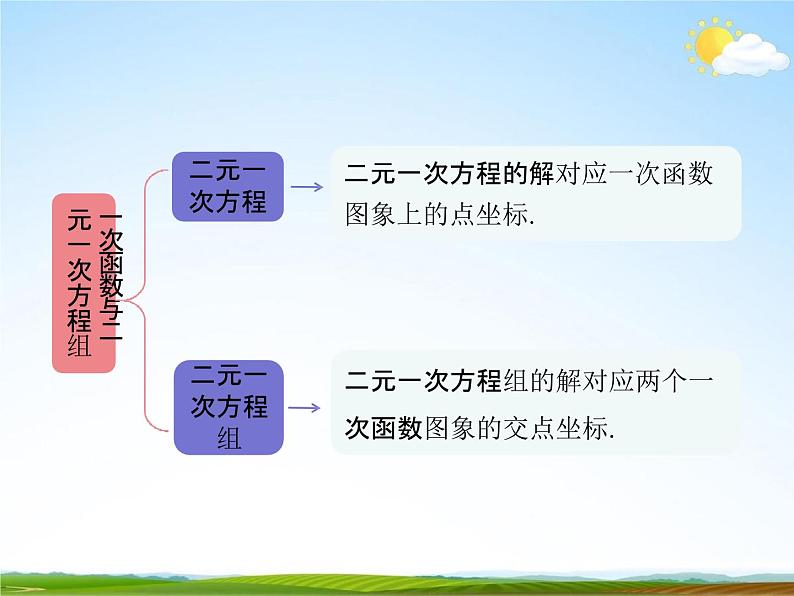
一次函数与二元一次方程组
二元一次方程的解对应一次函数 图象上的点坐标.
二元一次方程组的解对应两个一 次函数图象的交点坐标.
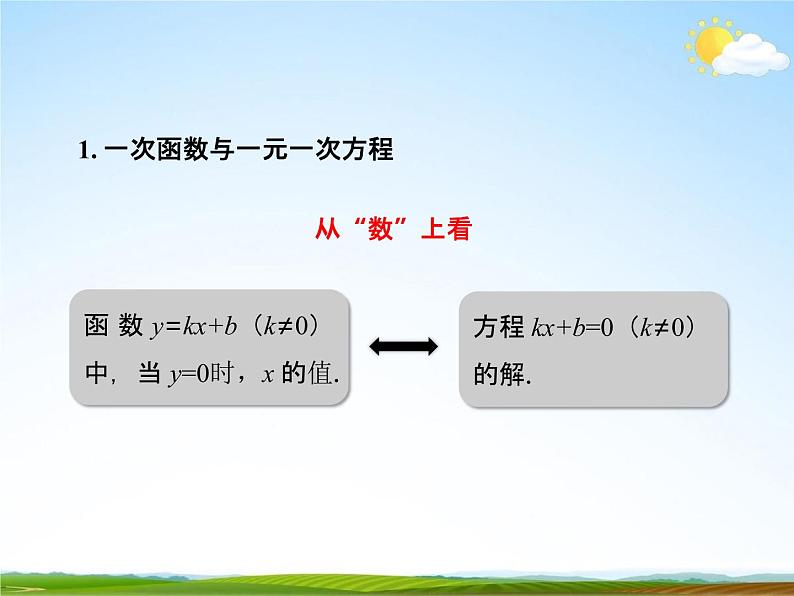
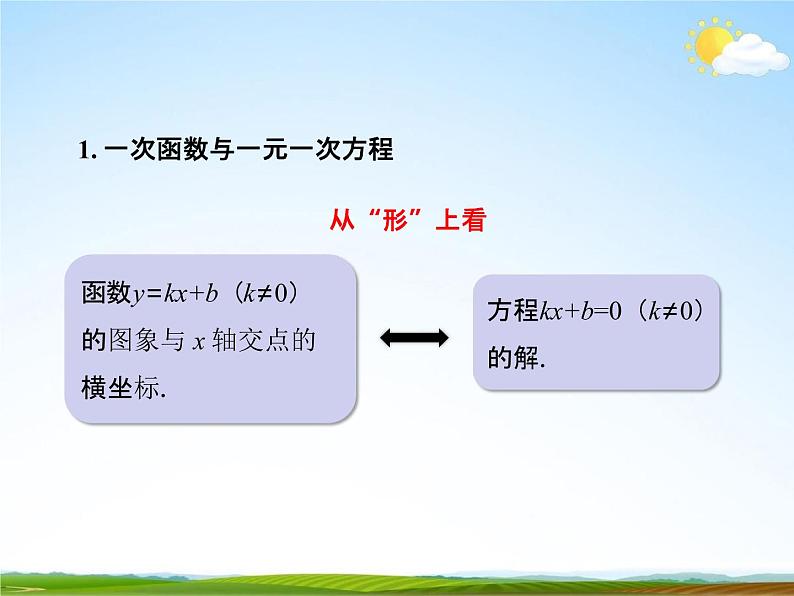
1. 一次函数与一元一次方程
函 数 y=kx+b（k≠0） 中，当 y=0时，x 的值.
方程 kx+b=0（k≠0） 的解.
函数 y=kx+b（k≠0） 的图象与 x 轴交点的 横坐标.
方程kx+b=0（k≠0） 的解.
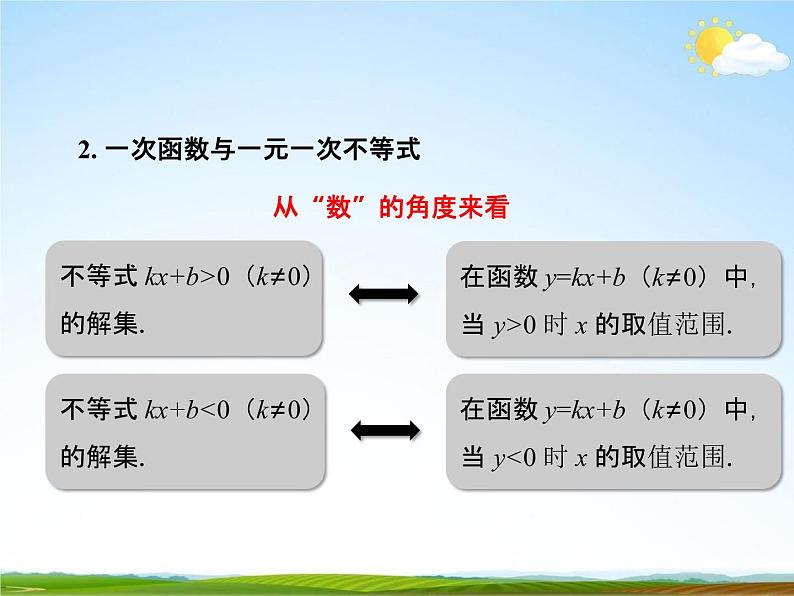
2. 一次函数与一元一次不等式从“数”的角度来看
不等式 kx+b>0（k≠0） 的解集.
在函数 y=kx+b（k≠0）中， 当 y>0 时 x 的取值范围.
不等式 kx+b<0（k≠0） 的解集.
在函数 y=kx+b（k≠0）中， 当 y<0 时 x 的取值范围.
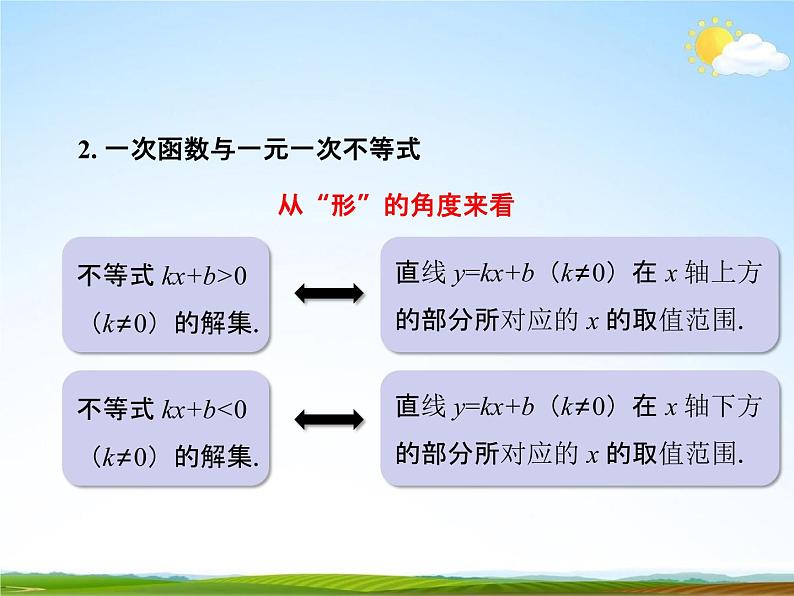
2. 一次函数与一元一次不等式从“形”的角度来看
不等式 kx+b>0（k≠0）的解集.
直线 y=kx+b（k≠0）在 x 轴上方 的部分所对应的 x 的取值范围.
不等式 kx+b<0（k≠0）的解集.
直线 y=kx+b（k≠0）在 x 轴下方 的部分所对应的 x 的取值范围.
3. 一次函数与二元一次方程（组）（1）一次函数 y=kx+b 的图象上任意一点的坐标都是 关于x、y 的二元一次方程 kx-y+b=0 的解；以二元一次 方程 kx-y+b=0 的解为坐标的点都在一次函数 y=kx+b 的图象上.
（a1、a2 、b1 、
a2 x+b2 y=c2
3. 一次函数与二元一次方程（组）a1 x+b1 y=c1
重难点1：一次函数与一元一次方程1.一元一次方程 ax-b=0 的解为 x=5，则函数 y=ax-b 与 x 轴
C.（5，0）D.（-5 ，0）解析：ax-b=0 的解就是当函数 y=ax-b 中 y=0 时 x 的值.
2.如图，一次函数y=2x+1的图象与坐标轴分别交于A、B两 点，O为坐标原点，则△AOB的面积是（ A）.
重难点2：一次函数与一元一次不等式已知一次函数 y=ax+b 与 x 轴、y 轴的交点坐标分别是（-2，0）、（0，4），则关于 x 的不等式 ax+b>0 的解集是（A）.
A.x>-2C.x>4
B. x<-2D.x<4
解析：ax+b>0 的解就是当函数 y=ax-b 中 y>0 时的 x的取值范围.
重难点3：一次函数与二元一次方程（组）
y=ax+b（-1，0）
2.用图象法解某二元一次方程组时，在同一直角坐标系中画 出相应的两个一次函数的图象，则所解的二元一次方程组是
解析：根据给出的图象上的点的坐标（0，2）、（1，1）、（0，-1），分别 求出图中两条直线的函数解析式为y=- x+2， y=2x-1，即x+y-2=0，2x-y-1=0.直接验证直线的交点是否满足二元一次方程组致错 这类问题的求解，如本题，不能只将交点P（1，1）代入 方程组进行验证，这样不够严谨.
由一次函数图象确定二元一次方程组的方法
解决由一次函数的图象确定二元一次方程组的问题， 一般先找到直线所经过的点，然后用待定系数法求 出两直线的函数解析式，再结合一次函数与二元一 次方程组的关系即得所求的二元一次方程组.
1.某家电集团生产某种型号的新家电，前期投资200万元， 每生产1台这种新家电，后期还需其他投资0.3万元，已知每 台新家电可实现产值0.5万元.（1）分别求出总投资额y1（万元）和总利润y2（万元）关于 新家电的总产量x（台）的函数解析式；
当新家电的总产量为900台时，该公司的盈亏情况如何？请你利用（1）中y2和x的函数解析式，分析该公司的盈 亏情况.
解：（1）根据题意可得： y1=0.3x+200， y2=0.5x-（0.3x+200）=0.2x-200.
提取等量关系列函数解析式本题中，与y1、x有关的等量关系为“总投资= 前期投资+后期投资”；与y2、x有关的等量关 系为“总利润=总产值-总投资”.
（2）把 x=900 代入 y2=0.2x-200，可得y2=-20<0.所以当新家电的总产量为 900 台时，公司会亏损，亏损的金额为 20 万元.
（3）由（1）得 y2=0.2x-200，令 y2<0，解得x<1000.说明总产量小于1000台时，公司会亏损. 令y2>0，解得x>1000.说明总产量大于1000台时，公司会盈利.令y2=0，解得x=1000.说明总产量等于1000台时，公司既不盈利也不亏损.
利用一次函数、一元一次方程和一元一次不等式 解决实际问题的策略解决此类实际应用问题，一定要结合实际问题， 提取等量关系，建立数学模型；二要结合所求， 建立方程或不等式，进而解方程或不等式；三要 结合求得的结果来回答实际问题，且要注意实际 问题中自变量的取值范围.
2.在“美丽家乡，清洁乡村”活动中，李家村村长提出两种 购买垃圾桶的方案，方案一：买分类垃圾桶，需要费用 3000 元，以后每月的垃圾处理费用为 250 元；方案二：买不分类垃圾桶，需要费用 1000 元，以后每月的垃圾处理费 用为 500 元.设方案一的购买费和垃圾处理费共 y1 元，方案 二的购买费和垃圾处理费共 y2 元，交费时间为 x 个月.（1）直接写出 y1、y2 与 x 的函数解析式；
在同一平面直角坐标系中，画出函数 y2、y2 的图象；在垃圾桶使用寿命相同的情况下，哪种方案更省钱？ 解：（1） 由题意可得：y1=250x+3000（x≥0）； y2=500x+1000（x≥0）.忽略实际问题中自变量的取值范围致错本题为实际应用题，自变量x的取值有一定的限制，即x≥0，因此在画函数图象时切忌把函数图象画成直线.
（2）对于 y1=250x+3000（x≥0），当 x=0 时，y1=3000；当 x=4 时，y1=4000 .过点（0，3000）、（4，4000）在第 一象限内画射线，即是函数 y1=250x+3000（x≥0）的图象.对于 y2=500x+1000（x≥0） ，当 x=0 时，y2=1000；当 x=4 时，y1=3000 .过点（0，1000）、（4，3000）在第 一象限内画射线，即是函数 y2=500x+1000（x≥0）的图象.
y1=250x+3000（x≥0），过点（0，3000）、（4，4000）； y2=500x+1000（x≥0），过点（0，1000）、（4，3000）.
解得x=8 y=5000
（3）解方程组y=250x+3000y=500x+1000
所以函数 y1=250x+3000（x≥0）、y2=500x+1000（x≥0） 的图象的交点坐标为（8，5000）.观察图象可得：当x>8时，y1y2，方案二更省钱.