

- 2021广东中考语文考前模拟信息卷(二)(PDF版含答案) 试卷 3 次下载
- 2021年广东省东莞中学中考数学一模试卷 试卷 5 次下载
- 2021年广东省深圳市中考物理模拟试卷一 试卷 3 次下载
- 广东2021年中考语文考前最后一卷 试卷 3 次下载
- 2021年广东省深圳市中考数学冲刺模拟试卷 试卷 1 次下载
2021年广东省深圳市中考数学全真模拟试卷
展开2021年广东省深圳市中考数学全真模拟试卷
一.选择题(共10小题,每题3分,共30分)
1.(3分)方程x(x﹣6)=0的解是( )
A.x=6 B.x1=0,x2=6 C.x=﹣6 D.x1=0,x2=﹣6
2.(3分)李老师为了解学生家务劳动时间情况,更好地弘扬“热爱劳动”的民族传统美德,随机调查了本校10名学生在上周参加家务劳动的时间,收集到如下数据(单位:小时):4,3,4,6,5,5,6,5,4,5.则这组数据的中位数和众数分别是( )
A.4,5 B.5,4 C.5,5 D.5,6
3.(3分)芯片是手机、电脑等高科技产品的核心部件,目前我国芯片已可采用14纳米工艺.已知14纳米为0.000000014米,数据0.000000014用科学记数法表示为( )
A.1.4×10﹣10 B.1.4×10﹣8 C.14×10﹣8 D.1.4×10﹣9
4.(3分)若在实数范围内有意义,则x的取值范围是( )
A.x≥﹣3 B.x≠﹣3 C.x≥3 D.x≠3
5.(3分)如图,▱ABCD的周长为52,对角线AC,BD相交于点O,点E是CD的中点,BD=18,则△DOE的周长是( )
A.22 B.26 C.31 D.35
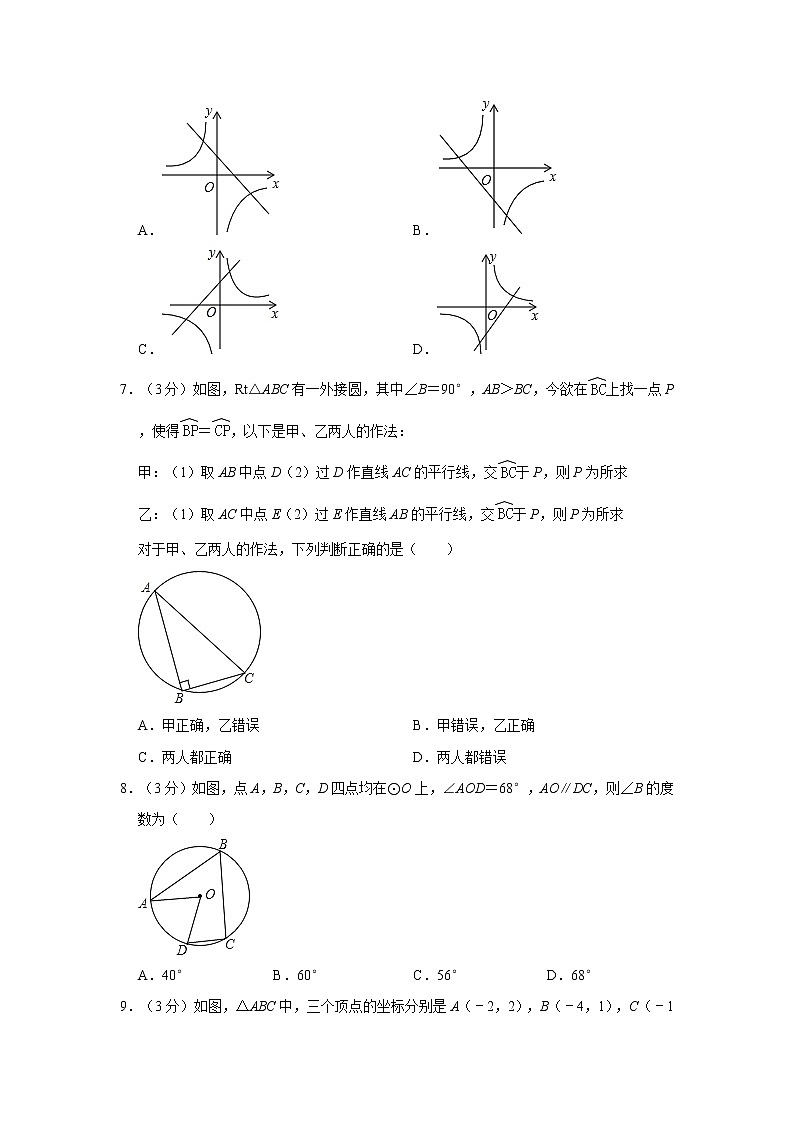
6.(3分)二次函数y=ax2+bx+c的图象如图所示,则反比例函数与一次函数y=bx+c在同一坐标系内的大致图象是( )
A. B.
C. D.
7.(3分)如图,Rt△ABC有一外接圆,其中∠B=90°,AB>BC,今欲在上找一点P,使得=,以下是甲、乙两人的作法:
甲:(1)取AB中点D(2)过D作直线AC的平行线,交于P,则P为所求
乙:(1)取AC中点E(2)过E作直线AB的平行线,交于P,则P为所求
对于甲、乙两人的作法,下列判断正确的是( )
A.甲正确,乙错误 B.甲错误,乙正确
C.两人都正确 D.两人都错误
8.(3分)如图,点A,B,C,D四点均在⊙O上,∠AOD=68°,AO∥DC,则∠B的度数为( )
A.40° B.60° C.56° D.68°
9.(3分)如图,△ABC中,三个顶点的坐标分别是A(﹣2,2),B(﹣4,1),C(﹣1,﹣1).以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',并把△ABC的边长放大为原来的2倍,那么点A'的坐标为( )
A.(3,﹣7) B.(1,﹣7) C.(4,﹣4) D.(1,﹣4)
10.(3分)已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合).且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个说法:
①△OEF是等腰直角三角形;②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是2+;④四边形OECF的面积是1.
其中正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
二.填空题(共5小题,每题3分,共15分)
11.(3分)分解因式:3x2﹣12x+12= .
12.(3分)掷一枚质地均匀的骰子,掷得的点数是合数的概率为 .
13.(3分)观察下列一组数:,﹣,,﹣,,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
14.(3分)如图,在x轴上方,平行于x轴的直线与反比例函数y=和y=的图象分别交于A、B两点,连接OA、OB.若△AOB的面积为6,则k2﹣k1= .
15.(3分)如图,CD是大半圆O的直径,点O1在CD上,大半圆的弦AB与小半圆O1相切于点F,且AB∥CD,AB=6,则阴影部分的面积为 .
三.解答题(共7小题,其中第16题6分,第17小题7分,第18小题7分,第19小题8分,第20小题8分,第21小题9分,第22小题10分,共55分)
16.(6分)计算:(2﹣)0+|﹣|﹣2cos45°+()﹣1.
17.(7分)先化简,再求值(﹣1)÷,其中x=2.
18.(7分)某校七、八年级各有400名学生,为了了解疫情期间线上教学学生的学习情况,复学后,某校组织了一次数学测试,刘老师分别从七、八两个年级随机抽取各50名同学的成绩(百分制),并对数据(成绩)进行了整理、描述和分析,部分信息如下:
a.七、八年级的频数分布直方图如下(数据分为5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
b.七年级学生成绩在80≤x<90的这一组是:
80 80 81 81 81 82 82 82 83
85 85 86 86 88 88 89 90 90
c.七、八年级学生成绩的平均数、中位数如下:
年级
平均数
中位数
七年级
80.3
m
八年级
78.2
76
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)在这次测试中,八年级80分以上(含80分)有 人;
(3)小江说:“这次考试没考好,只得了79分,但年级排名仍属于前50%”,请判断小江所在年级,并说明理由;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.
19.(8分)如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(≈1.414,≈1.732,结果精确到0.1海里)
20.(8分)如图1,AC是平行四边形ABCD的对角线,E、H分别为边BA和边BC延长线上的点,连接EH交AD、CD于点F、G,且EH∥AC.
(1)求证:△AEF≌△CGH;
(2)若△ACD是等腰直角三角形,∠ACD=90°,F是AD的中点,AD=8,求BE的长;
(3)在(2)的条件下,连接BD,如图2,求证:AC2+BD2=2(AB2+BC2).
21.(9分)已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,连接CE,BD是⊙O的切线与OE的延长线相交于点D.
(1)求证:∠D=∠AEC;
(2)求证:CE2=EH•EA;
(3)若⊙O的半径为5,,求FH的长.
22.(10分)如图,抛物线y=ax2+bx+c的顶点C的坐标是(6,﹣4),它的图象经过点A(4,0),其对称轴与x轴交于点D.
(1)求该抛物线的解析式;
(2)若点E是抛物线对称轴上一动点,点F是y轴上一动点,且点E、F在运动过程中始终保持DF⊥OE,垂足为点N,连接CN,当CN最短时,求点N的坐标;
(3)连接AC(若点P是x轴下方抛物线上一动点(点P与顶点C不重合),过点P作PM⊥AC于点M,是否存在点P,使PM、CM的长度是2倍关系.若存在,求出此时点P的坐标;若不存在,说明理由.
2021年广东省深圳市中考数学全真模拟试卷
参考答案与试题解析
一.选择题(共10小题,每题3分,共30分)
1.(3分)方程x(x﹣6)=0的解是( )
A.x=6 B.x1=0,x2=6 C.x=﹣6 D.x1=0,x2=﹣6
【分析】根据因式分解法解一元二次方程即可求解.
【解答】解:x(x﹣6)=0
x=0或x﹣6=0
解得x1=0,x2=6.
故选:B.
2.(3分)李老师为了解学生家务劳动时间情况,更好地弘扬“热爱劳动”的民族传统美德,随机调查了本校10名学生在上周参加家务劳动的时间,收集到如下数据(单位:小时):4,3,4,6,5,5,6,5,4,5.则这组数据的中位数和众数分别是( )
A.4,5 B.5,4 C.5,5 D.5,6
【分析】根据中位数、众数的意义和计算方法进行计算即可.
【解答】解:这组数据4,3,4,6,5,5,6,5,4,5中,出现次数最多的是5,因此众数是5,
将这组数据从小到大排列为:3,4,4,4,5,5,5,5,6,6,处在第5、6位的两个数都是5,因此中位数是5.
故选:C.
3.(3分)芯片是手机、电脑等高科技产品的核心部件,目前我国芯片已可采用14纳米工艺.已知14纳米为0.000000014米,数据0.000000014用科学记数法表示为( )
A.1.4×10﹣10 B.1.4×10﹣8 C.14×10﹣8 D.1.4×10﹣9
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:0.000000014=1.4×10﹣8.
故选:B.
4.(3分)若在实数范围内有意义,则x的取值范围是( )
A.x≥﹣3 B.x≠﹣3 C.x≥3 D.x≠3
【分析】根据被开方数大于等于0列式求解即可.
【解答】解:根据题意得,2x﹣6≥0,
解得x≥3.
故选:C.
5.(3分)如图,▱ABCD的周长为52,对角线AC,BD相交于点O,点E是CD的中点,BD=18,则△DOE的周长是( )
A.22 B.26 C.31 D.35
【分析】利用平行四边形的性质,三角形中位线定理即可解决问题.
【解答】解:∵平行四边形ABCD的周长为52,
∴BC+CD=26,
∵OD=OB,DE=EC,
∴OE+DE=(BC+CD)=13,
∵BD=18,
∴OD=BD=9,
∴△DOE的周长为13+9=22.
故选:A.
6.(3分)二次函数y=ax2+bx+c的图象如图所示,则反比例函数与一次函数y=bx+c在同一坐标系内的大致图象是( )
A. B.
C. D.
【分析】根据二次函数图象与系数的关系,由抛物线对称轴的位置确定a>0,b>0,由抛物线与y轴的交点位置确定c<0,然后利用排除法即可得出正确答案.
【解答】解:∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象的对称轴在y轴的左侧,且交y轴的负半轴,
∴b>0,c<0,
∴反比例函数y=的图象必在一、三象限,一次函数y=bx+c的图象必经过一三四象限,故D正确.
故选:D.
7.(3分)如图,Rt△ABC有一外接圆,其中∠B=90°,AB>BC,今欲在上找一点P,使得=,以下是甲、乙两人的作法:
甲:(1)取AB中点D(2)过D作直线AC的平行线,交于P,则P为所求
乙:(1)取AC中点E(2)过E作直线AB的平行线,交于P,则P为所求
对于甲、乙两人的作法,下列判断正确的是( )
A.甲正确,乙错误 B.甲错误,乙正确
C.两人都正确 D.两人都错误
【分析】(1)由甲的作法可知,DP是△ABC的中位线,由于DP不垂直于BC,故≠;
(2)由乙的作法,连BE,可知△BEC为等腰三角形,由等腰三角形的性质可知∠1=∠2,根据圆周角定理即可得出结论
【解答】解:(1)由甲的作法可知,DP是△ABC的中位线,
∵DP不垂直于BC,
∴≠;
(2)由乙的作法,连BE,可知△BEC为等腰三角形
∵直线PE⊥BC,
∴∠1=∠2
故=;
∴甲错误,乙正确.
故选:B.
8.(3分)如图,点A,B,C,D四点均在⊙O上,∠AOD=68°,AO∥DC,则∠B的度数为( )
A.40° B.60° C.56° D.68°
【分析】接OC,由AO∥DC,得出∠ODC=∠AOD=68°,再由OD=OC,得出∠ODC=∠OCD=68°,求得∠COD=44°,进一步得出∠AOC,进一步利用圆周角定理得出∠B的度数即可.
【解答】解:如图,
连接OC,
∵AO∥DC,
∴∠ODC=∠AOD=68°,
∵OD=OC,
∴∠ODC=∠OCD=68°,
∴∠COD=44°,
∴∠AOC=112°,
∴∠B=∠AOC=56°.
故选:C.
9.(3分)如图,△ABC中,三个顶点的坐标分别是A(﹣2,2),B(﹣4,1),C(﹣1,﹣1).以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',并把△ABC的边长放大为原来的2倍,那么点A'的坐标为( )
A.(3,﹣7) B.(1,﹣7) C.(4,﹣4) D.(1,﹣4)
【分析】建立以C为坐标原点的平面直角坐标系,根据位似变换的性质解答即可.
【解答】解:以C为坐标原点建立平面直角坐标系,则点A在新坐标系中的坐标为(﹣1,3),
∵△ABC与△A'B'C'以点C为位似中心,在x轴下方作△ABC的位似图形△A'B'C',把△ABC的边长放大为原来的2倍,
∴点A'在新坐标系中的坐标为(1×2,﹣3×2),即(2,﹣6),
则点A'的坐标为(1,﹣7),
故选:B.
10.(3分)已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合).且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个说法:
①△OEF是等腰直角三角形;②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是2+;④四边形OECF的面积是1.
其中正确的是( )
A.①②③ B.③④ C.①②④ D.①②③④
【分析】①易证得△OBE≌△OCF(SAS),则可证得结论①正确;
②由OE的最小值是O到BC的距离,即可求得OE的最小值1,根据三角形面积公式即可判断选项②正确;
③利用勾股定理求得≤EF<2,即可求得选项③正确;
④证明△OBE≌△OCF,根据正方形被对角线将面积四等分,即可得出选项④正确.
【解答】解:①∵四边形ABCD是正方形,AC,BD相交于点O,
∴OB=OC,∠OBC=∠OCD=45°,
在△OBE和△OCF中,
∴△OBE≌△OCF(SAS),
∴OE=OF,
∵∠BOE=∠COF,
∴∠EOF=∠BOC=90°,
∴△OEF是等腰直角三角形;
故①正确;
②∵当OE⊥BC时,OE最小,此时OE=OF=BC=1,
∴△OEF面积的最小值是=,
故②正确;
③∵BE=CF,
∴CE+CF=CE+BE=BC=2,
设EC=x,则BE=CF=2﹣x,
∴EF==,
∵0<x<2,
∴≤EF<2,
∵<<2,
∴存在一个△ECF,使得△ECF的周长是2+,
故③正确;
④由①知:△OBE≌△OCF,
∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBC=S正方形ABCD=×2×2=1,
故④正确;
故选:D.
二.填空题(共5小题,每题3分,共15分)
11.(3分)分解因式:3x2﹣12x+12= 3(x﹣2)2 .
【分析】原式提取3后,利用完全平方公式分解即可.
【解答】解:原式=3(x2﹣4x+4)=3(x﹣2)2,
故答案为:3(x﹣2)2
12.(3分)掷一枚质地均匀的骰子,掷得的点数是合数的概率为 .
【分析】根据概率的求法,找准两点:
①全部情况的总数;
②符合条件的情况数目;二者的比值就是其发生的概率.
【解答】解:掷一枚质地均匀的骰子,掷得的点数可能是1、2、3、4、5、6中的任意一个数,
共有六种可能,其中4、6是合数,
所以概率为=.
故答案为:.
13.(3分)观察下列一组数:,﹣,,﹣,,…,它们是按一定规律排列的,那么这一组数的第n个数是 (﹣1)n+1• .
【分析】根据题目中的数字,可以发现数字的分子和分母的变化特点,从而可以写出第n个数.
【解答】解:∵一组数:,﹣,,﹣,,…,
∴这组数为:,﹣,,﹣,,…,
∴这一组数的第n个数是(﹣1)n+1•,
故答案为:(﹣1)n+1•.
14.(3分)如图,在x轴上方,平行于x轴的直线与反比例函数y=和y=的图象分别交于A、B两点,连接OA、OB.若△AOB的面积为6,则k2﹣k1= 12 .
【分析】根据AB∥x轴,设设A(x,),B(,),得到AB=﹣x,根据△AOB的面积为6,列方程即可得到结论.
【解答】解:∵AB∥x轴,
∴设A(x,),B(,)
∴AB=﹣x,
∵△AOB的面积为6,
∴(﹣x)•=6,
∴k2﹣k1=12,
故答案为:12.
15.(3分)如图,CD是大半圆O的直径,点O1在CD上,大半圆的弦AB与小半圆O1相切于点F,且AB∥CD,AB=6,则阴影部分的面积为 π .
【分析】阴影部分的面积等于大半圆面积减去小半圆面积,根据垂径定理和勾股定理求解.
【解答】解:设大圆圆心为O,作EO⊥AB,垂足为E.
连接OA,则OA是大圆半径,
∵AB∥CD,
∴EO的长等于小圆的半径,
由垂径定理知,点E是AB的中点.
由勾股定理知,OA2﹣EO2=AE2=9,
∴阴影部分的面积=(OA2﹣EO2)π=π.
故答案为:π.
三.解答题(共7小题,其中第16题6分,第17小题7分,第18小题7分,第19小题8分,第20小题8分,第21小题9分,第22小题10分,共55分)
16.(6分)计算:(2﹣)0+|﹣|﹣2cos45°+()﹣1.
【分析】直接利用负整数指数幂的性质和零指数幂的性质分别化简得出答案.
【解答】解:原式=1+﹣2×+3
=1+﹣+3
=4.
17.(7分)先化简,再求值(﹣1)÷,其中x=2.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.
【解答】解:原式=(﹣)÷
=•
=,
当x=2时,原式=.
18.(7分)某校七、八年级各有400名学生,为了了解疫情期间线上教学学生的学习情况,复学后,某校组织了一次数学测试,刘老师分别从七、八两个年级随机抽取各50名同学的成绩(百分制),并对数据(成绩)进行了整理、描述和分析,部分信息如下:
a.七、八年级的频数分布直方图如下(数据分为5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
b.七年级学生成绩在80≤x<90的这一组是:
80 80 81 81 81 82 82 82 83
85 85 86 86 88 88 89 90 90
c.七、八年级学生成绩的平均数、中位数如下:
年级
平均数
中位数
七年级
80.3
m
八年级
78.2
76
根据以上信息,回答下列问题:
(1)表中m的值为 80 ;
(2)在这次测试中,八年级80分以上(含80分)有 20 人;
(3)小江说:“这次考试没考好,只得了79分,但年级排名仍属于前50%”,请判断小江所在年级,并说明理由;
(4)若85分及以上为“优秀”,请估计七年级达到“优秀”的人数.
【分析】(1)根据题意和直方图中的数据,可以求得m的值;
(2)根据题目中的数据和直方图中的数据,可以得到在这次测试中,八年级80分以上(含80分)的人数;
(3)根据表格中的数据,可以得到小江属于哪个年级,并说明理由;
(4)根据题目中的数据和直方图中的数据,可以计算出七年级达到“优秀”的人数.
【解答】解:(1)由直方图中的数据可知,
中位数是80≤x<90这一组第一个和第二个数的平均数,
故m=(80+80)÷2=80,
故答案为:80;
(2)由频数分布直方图可得,
在这次测试中,八年级80分以上(含80分)有17+3=20(人),
故答案为:20;
(3)小江属于八年级,因为小江的成绩大于八年级成绩的中位数,而小于七年级成绩的中位数,故小江属于八年级;
(4)400×=136(人),
即七年级达到“优秀”的有136人.
19.(8分)如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(≈1.414,≈1.732,结果精确到0.1海里)
【分析】(1)过点B作BH⊥CA交CA的延长线于点H,根据三角函数可求BH的长;
(2)根据勾股定理可求DH,在Rt△ABH中,根据三角函数可求AH,进一步得到AD的长.
【解答】解:(1)过点B作BH⊥CA交CA的延长线于点H(如图),
∵∠EBC=60°,
∴∠CBA=30°,
∵∠FAD=30°,
∴∠BAC=120°,
∴∠BCA=180°﹣∠BAC﹣∠CBA=30°,
∴BH=BC×sin∠BCA=150×=75(海里),
答:B点到直线CA的距离是75海里;
(2)∵BD=75海里,BH=75海里,
∴DH==75(海里),
∵∠BAH=180°﹣∠BAC=60°,
在Rt△ABH中,tan∠BAH==,
∴AH=25,
∴AD=DH﹣AH=75﹣25≈31.7(海里),
答:执法船从A到D航行了31.7海里.
20.(8分)如图1,AC是平行四边形ABCD的对角线,E、H分别为边BA和边BC延长线上的点,连接EH交AD、CD于点F、G,且EH∥AC.
(1)求证:△AEF≌△CGH;
(2)若△ACD是等腰直角三角形,∠ACD=90°,F是AD的中点,AD=8,求BE的长;
(3)在(2)的条件下,连接BD,如图2,求证:AC2+BD2=2(AB2+BC2).
【分析】(1)证明四边形ACHF是平行四边形,四边形ACGE是平行四边形,可得AC=HF=EG,AE=CG,AF=CH,即可推出EF=GH,根据SSS可得出△AEF≌△CGH;.
(2)首先证明∠BCF=90°,在Rt△BCF中,利用勾股定理可求出BF,则可求出答案;
(3)由平行四边形的性质及勾股定理可得出答案.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∵AC∥EH,
∴四边形ACHF是平行四边形,四边形ACGE是平行四边形,
∴AC=HF,AC=EG,AE=CG,AF=CH,
∴FH=EG,
∴EF=GH,
在△AEF和△CGH中,
,
∴△AEF≌△CGH(SSS);
(2)解:∵AD=8,F是AD的中点,
∴AF=AD=4,
∵四边形ACGE是平行四边形,∠ACD=90°,
∴四边形ACGE是矩形,
∴∠E=∠EAF=90°,
∴∠EAF=45°,
∴AE=EF=4×=2,
∵△ACD是等腰直角三角形,
∴CD=AB=8×=4,
∴BE=AB+AE=4+2=6;
(3)证明:如图,设AC与BD的交点为O,
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,AB∥CD,AB=CD,
∴BD=2OB,AC=2OA,
∴BD2=4OB2,
∵△ACD是等腰直角三角形,
∴∠BAC=∠ACD=90°,AC=CD,
∴OB2=AB2+OA2,AB=AC,
∴BD2=4AB2+4OA2=4AB2+AC2,
∴AC2+BD2=4AB2+2AC2,
∵AB2+AC2=BC2,
∴BC2=2AB2,
∴AC2+BD2=2(AB2+BC2).
21.(9分)已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,连接CE,BD是⊙O的切线与OE的延长线相交于点D.
(1)求证:∠D=∠AEC;
(2)求证:CE2=EH•EA;
(3)若⊙O的半径为5,,求FH的长.
【分析】(1)先判断出∠ABC+∠DBC=90°,再判断出∠DBC+∠D=90°即可;
(2)连接AC,如图所示,证明△CEH∽△AEC,由相似三角形的性质即可得出结论;
(3)连接BE,过O作OG⊥BE于G,由锐角三角函数的定义求出AE=8,根据勾股定理求出BE,求出EH,BH的长,由三角形面积求出BF的长,则可求出答案.
【解答】(1)证明:∵BD是⊙O的切线,
∴∠OBD=90°,∠ABC+∠DBC=90°,
∵BC⊥OD,
∴∠D+∠DBC=90°,
∴∠ABC=∠D,
∵∠AEC=∠ABC,
∴∠D=∠AEC;
(2)证明:连接AC,如图所示:
∵OF⊥BC,
∴,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴,
∴CE2=EH•EA;
(3)解:连接BE,过O作OG⊥BE于G,如图所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,
∴AB=10,
∵cos∠BCE=,
∴cos∠BAE==,
∴AE=8,
∴BE===6,
∵,
∴BE=CE=6,
∵CE2=EH•EA,
∴EH=,
在Rt△BEH中,BH=.
∵OG⊥BE,OB=OE,
∴BG=3,
∴OG===4,
∴BF•OE,
∴BF=,
∴HF=BH﹣BF=.
22.(10分)如图,抛物线y=ax2+bx+c的顶点C的坐标是(6,﹣4),它的图象经过点A(4,0),其对称轴与x轴交于点D.
(1)求该抛物线的解析式;
(2)若点E是抛物线对称轴上一动点,点F是y轴上一动点,且点E、F在运动过程中始终保持DF⊥OE,垂足为点N,连接CN,当CN最短时,求点N的坐标;
(3)连接AC(若点P是x轴下方抛物线上一动点(点P与顶点C不重合),过点P作PM⊥AC于点M,是否存在点P,使PM、CM的长度是2倍关系.若存在,求出此时点P的坐标;若不存在,说明理由.
【分析】(1)由题意可设抛物线的解析式为y=a(x﹣6)2﹣4,再将点A(4,0)代入,解得a的值,则可求得该抛物线的解析式;
(2)由题意可得点N是以OD为直径的圆上的一动点,设以OD为直径的圆的圆心为点G,连接CG,交⊙G于点N',此时CN'即为最短的CN,过点N'作N'B⊥x轴于点B,判定△GBN'∽△GDC,从而得比例式,解得N'B=,GB=,根据OB=OG+GB,求得OB,则可得点N的坐标;
(3)存在点P,使PM、CM的长度是2倍关系.分情况讨论:①当点P在抛物线的对称轴的右侧时,PM=2CM,△PCM∽△CAD,如图2,延长CP交x轴于点Q,设Q(m,0),则(m﹣4)2=(m﹣6)2+42,解得m的值,则可得点Q的坐标,用待定系数法求得直线CQ的解析式,将其与抛物线的解析式联立,即可解得点P的坐标;②当点P在抛物线对称轴的左侧时,CM=2PM,△PCM∽△ACD,如图3,过点A作AH⊥AC,交CP的延长线于点H,过点H作HK⊥x轴,交x轴于点K,判定△HCA∽△ACD,△AHK∽△CAD,用待定系数法求得直线CH的解析式,将其与抛物线的解析式联立,即可解得点P的坐标.
【解答】解:(1)由题意可设抛物线的解析式为y=a(x﹣6)2﹣4,
∵图象经过点A(4,0),
∴a(4﹣6)2﹣4=0,
∴a=1,
∴y=(x﹣6)2﹣4=x2﹣12x+32,
∴该抛物线的解析式为y=x2﹣12x+32;
(2)如图1,
∵点E、F在运动过程中始终保持DF⊥OE,
∴点N是以OD为直径的圆上的一动点,
设以OD为直径的圆的圆心为点G,连接CG,交⊙G于点N',此时CN'即为最短的CN,过点N'作N'B⊥x轴于点B,
由已知得OD=6,CD=4,
∴GD=3,CG=5,
∵N'B⊥x轴,CD⊥x轴,
∴N'B∥CD,
∴△GBN'∽△GDC,
∴,
∴N'B=,GB=,
∴OB=OG+GB
=3+
=,
∴点N的坐标为(,﹣);
(3)存在点P,使PM、CM的长度是2倍关系.
∵A(4,0),D(6,0),
∴AD=2,
∵,∠ADC=90°,
∴当PM、CM的长度是2倍关系时,△PCM与△ACD相似.
①当点P在抛物线的对称轴的右侧时,PM=2CM,△PCM∽△CAD,
如图2,延长CP交x轴于点Q,此时∠QCA=∠QAC,
∴QA=QC,
∴QA2=QC2,
设Q(m,0),则(m﹣4)2=(m﹣6)2+42,
解得m=9,
∴Q(9,0),
设直线CQ的解析式为y=kx+b(k≠0),将C(6,﹣4),Q(9,0)代入,得:
,
解得,
∴y=x﹣12,
联立,
解得(舍去),,
∴点P(,﹣);
②当点P在抛物线对称轴的左侧时,CM=2PM,△PCM∽△ACD,
如图3,过点A作AH⊥AC,交CP的延长线于点H,过点H作HK⊥x轴,交x轴于点K,
由勾股定理得AC==2,
∵AH⊥AC,PM⊥AC,
∴AH∥PM,
∴△PCM∽△ACH,
∵△PCM∽△ACD,
∴△HCA∽△ACD,
∴=,
∴,
∴AH=,
∵HK⊥x轴,AH⊥AC,
∴∠HKA=∠ADC=∠HAC=90°,
∴∠KAH+∠AHK=90°,∠CAD+∠KAH=90°,
∴∠AHK=∠CAD,
∴△AHK∽△CAD,
∴,
∴,
∴AK=2,KH=1,
∴H(2,﹣1),
设直线CH的解析式为y=mx+n(m≠0),将C(6,﹣4),H(2,﹣1)代入,得:
,
解得,
∴直线CH的解析式为y=﹣x+,
联立,
解得(舍去),,
∴点P(,﹣);
综上所述,满足条件的点P的坐标为(,﹣)或(,﹣).
广东省深圳市宝山区2022-2023学年中考数学全真模拟试卷含解析: 这是一份广东省深圳市宝山区2022-2023学年中考数学全真模拟试卷含解析,共12页。
广东省深圳市坪山区2021-2022学年中考数学全真模拟试卷含解析: 这是一份广东省深圳市坪山区2021-2022学年中考数学全真模拟试卷含解析,共19页。试卷主要包含了计算,下列计算正确的是等内容,欢迎下载使用。
2022年广东省深圳市罗芳中学中考数学全真模拟试卷含解析: 这是一份2022年广东省深圳市罗芳中学中考数学全真模拟试卷含解析,共20页。试卷主要包含了考生必须保证答题卡的整洁,下列各组数中,互为相反数的是等内容,欢迎下载使用。












