


数学八年级上册11.1.2 三角形的高、中线与角平分线评课课件ppt
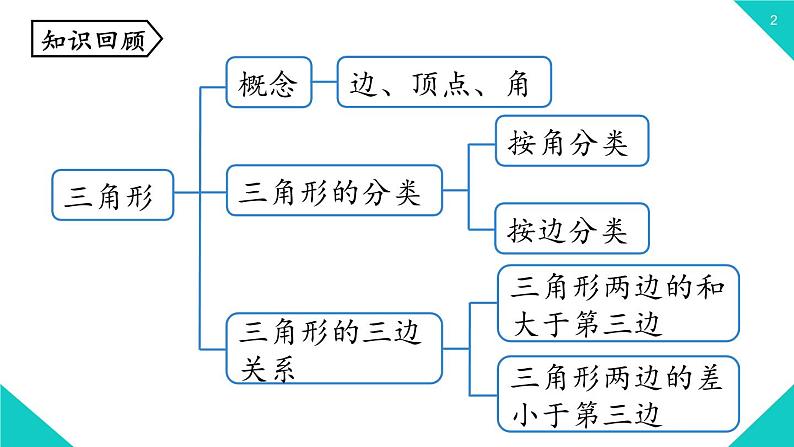
展开三角形两边的和大于第三边
三角形两边的差小于第三边
1.了解三角形的高、中线和角平分线的定义及画法.2.会利用三角形的高、中线和角平分线解决实际问题.
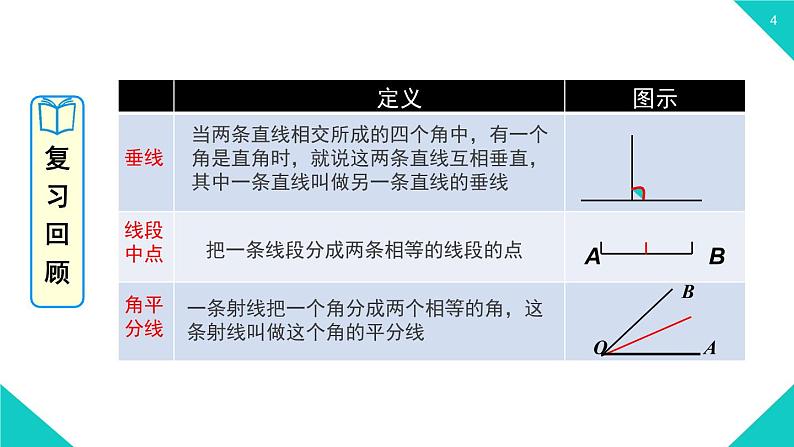
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
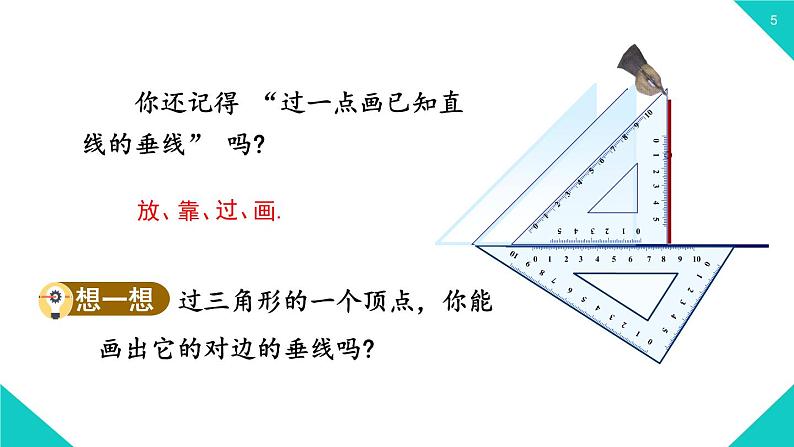
你还记得 “过一点画已知直线的垂线” 吗?
过三角形的一个顶点,你能画出它的对边的垂线吗?
定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的这条边上的高,这条对边叫做三角形的底.
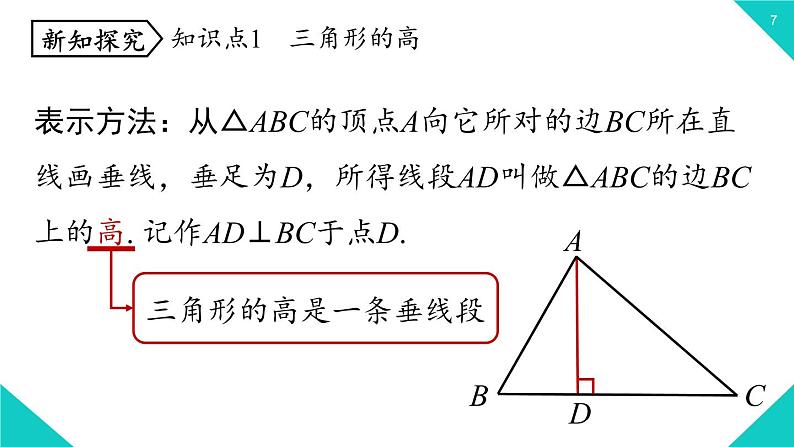
表示方法:从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高. 记作AD⊥BC于点D.
知识点1 三角形的高
三角形的高是一条垂线段
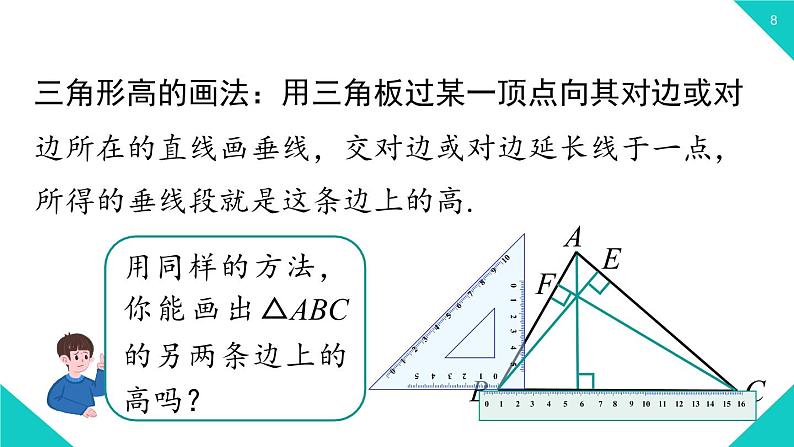
三角形高的画法:用三角板过某一顶点向其对边或对边所在的直线画垂线,交对边或对边延长线于一点,所得的垂线段就是这条边上的高.
例1 (1)下列图形中,AD是△ABC的高的是( )
(2) 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
解析:当BP⊥AC时,BP的值最小.∵S△ABC= BC·AD,S△ABC= AC·BP,∴ BC·AD= AC·BP ∴BC·AD=AC·BP∴6×4=5BP, BP= 所以BP的最小值为
例2 .[2021黑龙江齐齐哈尔建华区期末] 如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
1.定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.
知识点2 三角形的中线
如图,在△ABC中,AD是边BC上的中线,证明:△ABD和△ACD的面积相等.
3.画法:连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
4.画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.2.三角形的重心:三角形三条中线的交点.3.三角形的重心在各三角形中的位置:在三角形内部.4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如上图:AD为中线,则S△ABD=S△ACD.5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
例 3 如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )A.19 cm B.22 cm C.25 cm D.31 cm
解:∵AD是BC边上的中线, ∴BD=CD, ∴△ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC. ∵△ABD的周长为25 cm,AB比AC长6 cm, ∴△ACD的周长为25–6=19(cm).
如图,AD,BE,CF 是△ABC 的三条中线. (1)AC = AE ,AE=_____; CD = ; AF = AB; (2)若S△ABC = 12 cm2, 则S△ABD = .
(3)若AB=4,AC=3,则△ABD的周长与△ACD的周长之差是___.
例4 (1)如图,有一块三角形菜地,现要将其分成面积比为1∶1∶2的三块,已知点A处是三块菜地的共同水源处,则三块菜地应该怎么分?
解:根据面积比为1∶1∶2的要求,可以将三角形菜地的总面积看作4份.如图,作△ABC的中线AD,△ABD的中线AE,所得到的△ABE,△AED,△ADC的面积比就是1∶1∶2.
三角形的中线可以将三角形分成面积相等的两个小三角形
利用三角形的中线面积问题
(2):如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
问题1 如图,若OC是∠AOB的平分线,你能得到什么结论?
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
相同点是: ∠ABD= ∠ CBD;不同点是:前者是线段,后者是射线.
知识点3 三角形的角平分线
1.定义:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
3.画法:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.
例5 (1)如图,AD,BE,CF分别是△ABC的三条角平分线,请根据图中各角之间的关系填空:
(1)∠1=∠( );(2)∠3= ( );(3)∠ACB=( )∠4.
利用三角形的角平分线求角的度数
解:∵AD是△ABC的角平分线,∠BAC=68°, ∴∠DAC=∠BAD=34°. 在△ABD中,∠B+∠ADB+∠BAD=180°, ∴∠ADB=180°–∠B–∠BAD =180°–36°–34° =110°.
(2) 如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
钝角三角形两短边上的高的画法
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
1.如图,在△ABC中,∠1=∠2=∠3=∠4,则下列说法中,正确的是( )A.AD是△ABE的中线B.AE是△ABC的角平分线C.AF是△ACE的高线D.AE是△ABC的中线
∠1+∠2=∠3+∠4
(4)当BE=8,AF=7时,求△ABC的面积.
3.如图所示,已知△ABC的周长为27 cm,AC=9 cm,BC边上的中线AD为6 cm,△ABD的周长为19 cm,AB= .
AB+BC+AC=27 cm,AC=9 cm
AB+BD+AD=19 cm,AD=6 cm
AB+BC=18 cm
AB+BD=13 cm
1.(2021•重庆江津区校级期中)如图,在△ABC中,AD是边BC上的高,AE是角平分线. 若∠B=80°,∠C=30°,求∠DAE.
∵AD是边BC上的高,∴∠BAD=90°-∠B=10°,∴∠DAE=∠BAE-∠BAD=35°-10°=25°.
2.[2021四川绵阳东辰国际学校月考]如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则图中阴影部分的面积等于 ( )A.1 cm2 B.2 cm2C.4 cm2 D.6 cm2
人教版八年级上册11.1.2 三角形的高、中线与角平分线集体备课课件ppt: 这是一份人教版八年级上册11.1.2 三角形的高、中线与角平分线集体备课课件ppt,共28页。PPT课件主要包含了AP与BC垂直,AP是三角形的高,∠APC90°,相交于一点,画出或者折出高,画钝角三角形的高,任意一顶点,对边的延长线,不相交,三角形内部等内容,欢迎下载使用。
人教版八年级上册11.1.2 三角形的高、中线与角平分线优秀课件ppt: 这是一份人教版八年级上册11.1.2 三角形的高、中线与角平分线优秀课件ppt,文件包含1112《三角形的高中线与角平分线》课件-人教版数学八上pptx、1112《三角形的高中线与角平分线》教案-人教版数学八上docx等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
初中数学人教版八年级上册11.1.2 三角形的高、中线与角平分线图文ppt课件: 这是一份初中数学人教版八年级上册11.1.2 三角形的高、中线与角平分线图文ppt课件,共22页。PPT课件主要包含了学习目标,自学指导,三角形的高,三角形的中线,三角形的角平分线,角平分线的理解,课堂练习,感悟与反思等内容,欢迎下载使用。












