数学北师大版第一章 特殊平行四边形2 矩形的性质与判定导学案

章节 矩形的性质和判定        

 一：知识点回顾:

平行四边形的性质

(1)定义：两组对边分别平行的四边形是平行四边形．

(3)平行四边形性质1　　平行四边形的对边相等．

   平行四边形性质2    平行四边形的对角相等．

   平行四边形性质3   平行四边形的对角线互相平分．

平行四边形的判定：

1）定义:两组对边分别平行的四边形是平行四边形，是平行四边形.

2）定理:两组对边分别相等的四边形是平行四边形，是平行四边形.

3）定理:一组对边平行且相等的四边形是平行四边形，是平行四边形.

4）定理:对角线互相平分的四边形是平行四边形.，是平行四边形.

5）定理:两组对角分别相等的四边形是平行四边形，是平行四边形.

二：课堂引入

例1生活中常见的矩形有哪些？

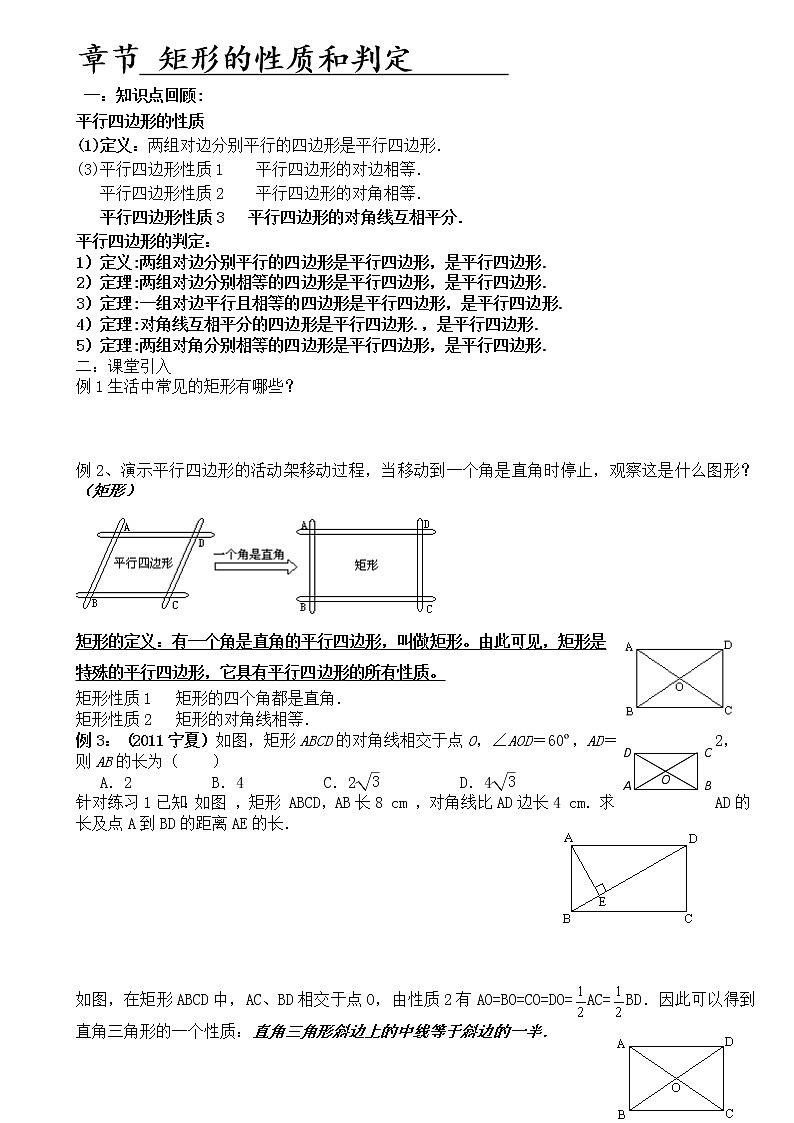
例2、演示平行四边形的活动架移动过程，当移动到一个角是直角时停止，观察这是什么图形？（矩形）

矩形的定义：有一个角是直角的平行四边形，叫做矩形。由此可见，矩形是特殊的平行四边形，它具有平行四边形的所有性质。

矩形性质1　 矩形的四个角都是直角．

矩形性质2　 矩形的对角线相等．

例3：（2011宁夏）如图，矩形ABCD的对角线相交于点O，∠AOD＝60º，AD＝2，

则AB的长为（    ）

A．2          B．4          C．2          D．4

针对练习1已知：如图 ，矩形 ABCD，AB长8 cm ，对角线比AD边长4 cm．求AD的长及点A到BD的距离AE的长．

如图，在矩形ABCD中，AC、BD相交于点O，由性质2有AO=BO=CO=DO=AC=BD．因此可以得到直角三角形的一个性质：直角三角形斜边上的中线等于斜边的一半．

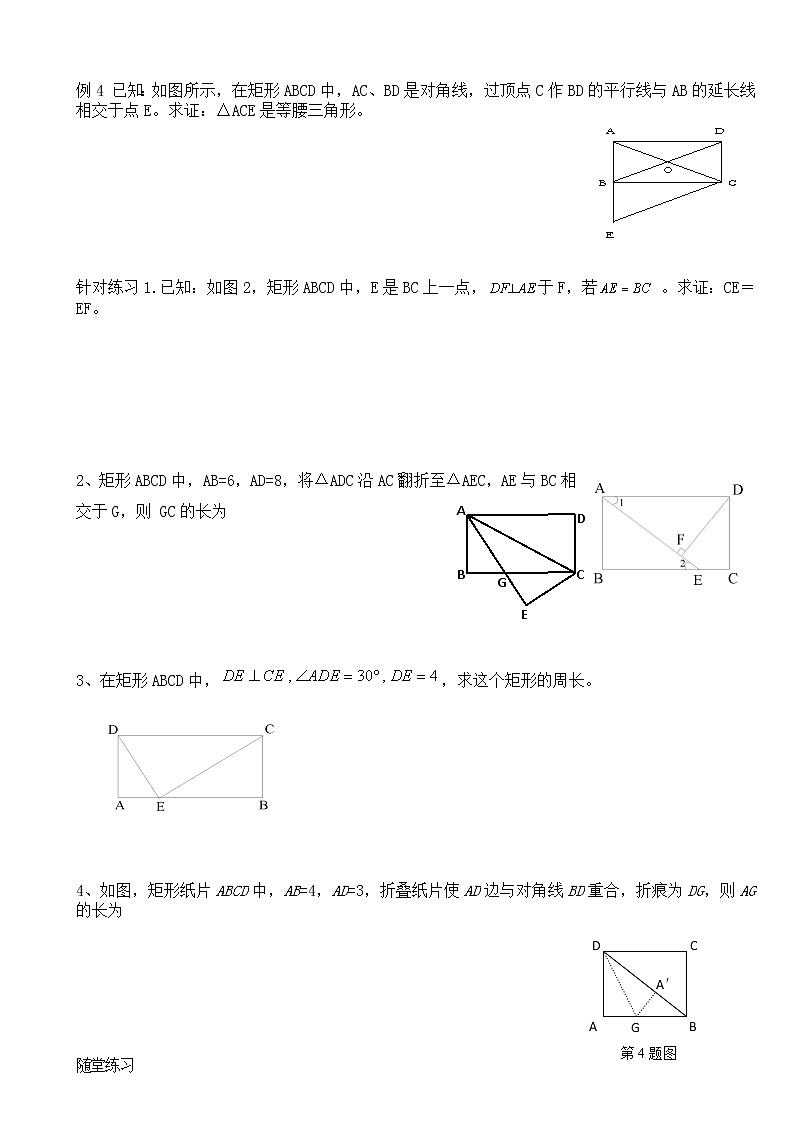
例4 已知：如图所示，在矩形ABCD中，AC、BD是对角线，过顶点C作BD的平行线与AB的延长线相交于点E。求证：△ACE是等腰三角形。

针对练习1.已知：如图2，矩形ABCD中，E是BC上一点，于F，若 。求证：CE＝EF。

2、矩形ABCD中，AB=6，AD=8，将ΔADC沿AC翻折至ΔAEC，AE与BC相交于G，则 GC的长为

3、在矩形ABCD中，，求这个矩形的周长。

4、如图，矩形纸片ABCD中，AB=4，AD=3，折叠纸片使AD边与对角线BD重合，折痕为DG，则AG的长为

随堂练习

1．（填空）

（1）矩形的定义中有两个条件：一是              ，二是                ．

（2）已知矩形的一条对角线与一边的夹角为30°，则矩形两条对角线相交所得的四个角的度数分别为        、        、        、        ．

（3）已知矩形的一条对角线长为10cm，两条对角线的一个交角为120°，则矩形的边长分别为        cm，        cm，        cm，        cm．

2．（选择）

（1）下列说法错误的是（    ）．

（A）矩形的对角线互相平分   （B）矩形的对角线相等步为营

（C）有一个角是直角的四边形是矩形  （D）有一个角是直角的平行四边形叫做矩形

（2）矩形的对角线把矩形分成的三角形中全等三角形一共有（     ）．

（A）2对   （B）4对  （C）6对  （D）8对

（选做题）3．已知：如图，O是矩形ABCD对角线的交点，AE平分∠BAD，∠AOD=120°，求∠AEO的度数．

矩形的判定定理

矩形的判定1：对角线相等的平行四边形是矩形

例1、平行四边形ABCD中，对角线AC、BD相交于点Ｏ，点Ｐ是四边形外一点，且PA⊥PC，PB⊥PD，垂足为Ｐ。求证：四边形ABCD为矩形。

矩形的判定2：有一个角是直角的平行四边形是矩形

例2、在平行四边形ABCD中，对角线AC、BD相交于O，EF过点O，且AF⊥BC，求证：四边形AFCE是矩形

矩形的判定3：有三个角是直角的四边形是矩形

例3已知：如图，平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H，求证：四边形 EFGH为矩形．

【提高练习】：

1、在矩形ABCD中，对角线AC，BD相交于点O，若对角线AC=10cm，边BC=8cm，则△ABO的周长为________．

2、矩形的一内角平分线把矩形的一条边分成3和5两部分，则该矩形的周长是（    ）

A.16   B.22   C.26   D.22或26

3、已知，在矩形ABCD中，AE⊥BD，E是垂足，

∠DAE∶∠EAB=2∶1，求∠CAE的度数.

4、如图，在矩形ABCD中，E是AD的中点，且EB⊥EC．

若矩形ABCD的周长为48cm，则矩形ABCD的面积为_______cm2．

巩固练习

一、判断题

1．矩形是轴对称图形，对角线是它的对称轴．（  ）

2．平行四边形也是轴对称图形其对称轴也是对角线．（  ）

3．AD是直角三角形ABC的中线，那么AD就等于它斜边BC的一半．（  ）

二、选择题

4．矩形ABCD的长为5，宽为3，点E、F将AC三等分，则△BEF的面积为（  ）．

    A．        D．5

5．已知矩形ABCD的AB=2BC，在CD上取点E，使AE=EB，那么∠EBC等于（  ）．

    A．60°     B．45°     C．30°     D．15°

6．如图1所示，矩形ABCD的对角线交于O，AE⊥BD于E，∠1：∠2=2：1，则∠1的度数为（  ）．

A．22．5°     B．45°     C．30°     D．60°

     (1)              (2)              (3)              (4)

7．下列叙述错误的是（  ）．

    A．平行四边形的对角线互相平分   B．对角线互相平分的四边形是平行四边形

    C．矩形的对角线相等              D．对角线相等的四边形是矩形

8．下列性质矩形不一定具备的是（  ）．

    A．对角线相等  B．四个内角都相等  C．对角线互相平分D．对角线互相垂直

三、填空题

9．如图2所示，O为矩形ABCD的对角线交点，DF平分∠ADC交AC于E，BC于F，∠BDF=15°，则∠COF=______．

10．若矩形两邻边之比为3：4，周长为28cm，则它的边长为______．

11．矩形ABCD的周长为40cm，O是它的对角线交点，△AOB比△AOD周长多4cm，则它的各边长之比为________．

12．如图3所示，矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠BAE=_____，∠EAD=_____，

∠EAC=_____．

  四、解答题

1、已知：矩形ABCD，M是BC的中点，BC＝2AB。求证：。

2、矩形的对角线的一个交角是，一条对角线长为8cm。求矩形的边长。

3．如图所示，矩形ABCD中，对角线AC、BD交于O点，CE⊥BD于E，OF⊥AB于F，BE：DE=1：3，OF=2cm，求AC的长．

4．如图所示，矩形ABCD中，长为7，宽为6，点E、F将BD三等分，求△AEF的面积．

选做题：

1、已知的两条高线BE、CF；M为BC中点，N为EF中点。求证：。

2、已知矩形ABCD中，F在CB延长线上，AE＝EF，CF＝CA。  求证：。