初中24.2.2 直线和圆的位置关系授课课件ppt

这是一份初中24.2.2 直线和圆的位置关系授课课件ppt，共25页。PPT课件主要包含了画一画，切线长定理，知识点1，切线长概念，比一比，折一折，PAPB，∠APO∠BPO，∠OPA∠OPB，几何语言等内容，欢迎下载使用。

情景：如图，纸上有一个⊙O, PA为⊙O的一条切线，沿着直线PO将纸对折，设与点A重合的点为B.
问题1：OB是⊙O的半径吗？PB是⊙O的切线吗？问题2：猜一猜图中的PA与PB有什么关系？∠APO与∠BPO有什么关系？
(1)知道什么是圆的切线长，能叙述并证明切线长定理.(2)会作三角形的内切圆，知道三角形内心的含义和性质.(3)能用切线长定理和三角形内心的性质来解决简单的问题.
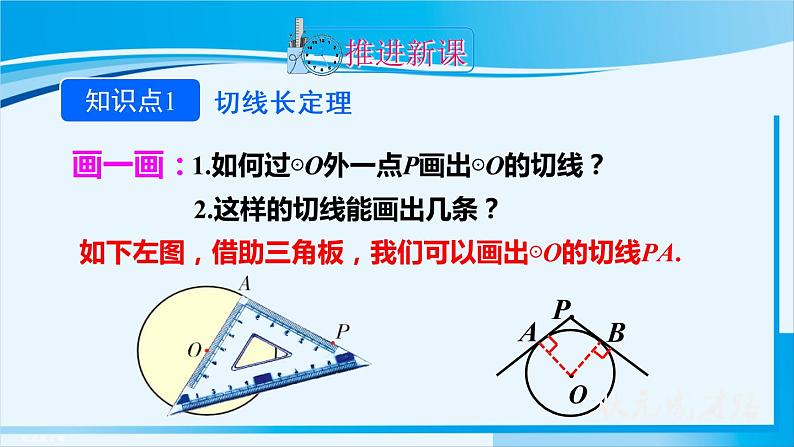
1.如何过⊙O外一点P画出⊙O的切线？
2.这样的切线能画出几条？
如下左图，借助三角板，我们可以画出⊙O的切线PA.
经过圆外一点的圆的切线上，这点和切点之间的线段的长叫做这点到圆的切线长.
切线与切线长有什么区别与联系呢？
切线和切线长是两个不同的概念：1.切线是一条与圆相切的直线；2.切线长是线段的长，这条线段的两个端点分别是圆外一点和切点.
如图，PA、PB是⊙O的两条切线，切点分别为A、B，将⊙O沿着直线OP对折，图中的PA与PB，∠APO与∠ BPO有什么关系?
请证明你所发现的结论.
证明：∵PA，PB与⊙O相切，点A，B是切点.∴OA⊥PA，OB⊥PB，即∠OAP=∠OBP=90°.∵ OA=OB，OP=OP，∴Rt△AOP≌Rt△BOP(HL).∴ PA = PB，∠OPA=∠OPB.
试用文字语言叙述你所发现的结论.
PA、PB分别切⊙O于A、B
从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.
切线长定理为证明线段相等、角相等提供新的方法.
探究：PA、PB是⊙O的两条切线，A、B为切点，直线OP交于⊙O于点D、E，交AB于C.
（1）写出图中所有的垂直关系；
OA⊥PA，OB ⊥PB，AB ⊥OP
（3）写出图中所有的全等三角形；
△AOP≌ △BOP， △AOC≌ △BOC， △ACP≌ △BCP
（4）写出图中所有的等腰三角形；
△ABP △AOB
（2）写出图中与∠OAC相等的角和图中相等的线段；
∠OAC=∠OBC=∠APC=∠BPC，OA=OB=OD=OE,PA=PB,AC=BC.
我们学过的切线，常有 五个 性质：1.切线和圆只有一个公共点；2.切线和圆心的距离等于圆的半径；3.切线垂直于过切点的半径；4.经过圆心垂直于切线的直线必过切点；5.经过切点垂直于切线的直线必过圆心；
6.从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角.
如图，一张三角形的铁皮，如何在它上面截下一块圆形的用料，并且使圆的面积尽可能大呢?
外接圆圆心(外心)：三角形三边垂直平分线的交点.外接圆的半径：交点到三角形任意一个顶点的距离.
内切圆圆心(内心)：三角形三个内角平分线的交点.内切圆的半径：交点到三角形任意一边的垂直距离.
如图, △ABC的内切圆⊙O与BC 、CA、 AB 分别相交于点D 、 E 、 F ，且AB＝9，BC ＝14, CA ＝13,求AF、BD、CE的长.
解：设AF=x,则AE=x, CD=CE=AC-AE=13-x, BD=BF=AB-AF=9-x.由BD+CD=BC,可得(13-x)+(9-x)=14.解得，x=4.因此，AF=4，BD=5，CE=9.
1.如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=11cm，BC=14cm，CA=13cm，则AF的长为( )A.3cmB.4cm C.5cmD.9cm
2.如图，点O是△ABC的内心，若∠BAC=86°，则∠BOC=( )A.172° B.130° C.133° D.100°
3.如图，已知VP、VQ为⊙T的切线，P、Q为切点，若VP=3cm，则VQ= cm.若∠PVQ＝60°，则⊙T的半径PT＝ cm.
4.如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC=25°，求∠P的度数.解：由切线长定理可知PA=PB.∵PA是⊙O的切线.∴∠OAP=90°.∵∠BAC=25°,∴∠BAP=65°.又∵PA＝PB,∴∠BAP=∠ABP=65°.∴∠P=180°-∠BAP-∠ABP=50°.
5.如图，一个油桶靠在墙边，量得WY =1.65m， 并且XY⊥WY，这个油桶底面半径是多少?
解：设圆心为O，连接OW,OX.∵YW,YX均是⊙O的切线，∴OW⊥WY,OX⊥XY，又∵XY⊥WY,∴∠OWY＝∠OXY＝∠WYX＝90°，∴四边形OWYX是矩形，又∵OW=OX.∴四边形OWYX是正方形.∴OW=WY=1.65m.即这个油桶底面半径是1.65m.
6.△ABC的内切圆半径为r，△ABC的周长为l，求△ABC的面积.(提示：设△ABC的内心为O，连接OA、OB、OC)解：设△ABC的内心为O，连接OA、OB、OC.则S△ABC=S△AOB+S△BOC+S△AOC
7.如图，AB、BC、CD分别与⊙O相切于E、F、G三点，且AB∥CD，BO＝6cm，CO＝8cm，求BC的长. 
解：∵AB、BC、CD分别与⊙O相切，则OB平分∠EBF，DC平分∠FCG.∵AB∥CD,∴∠EBF+∠GCF=180°.∴∠BOC=180°-∠OBF-∠OCF =90°. 
1.如图，PA,PB为⊙O切线，你能得到哪些信息？
(1)PA=PB；(2)OA⊥PA,OB⊥PB；(3)OP平分∠AOB和∠APB；(4)OP垂直平分AB.
连接AB以后，还能得到哪些信息？
2.如图，⊙O内切于△ABC,交点分别为D、E、F，你能得到哪些信息？
(1)AB⊥OD,BC⊥OF, AC⊥OE.(2)AO、BO、CO分别平分∠A 、∠B和∠C.