数学九年级上册22.3 实际问题与二次函数备课ppt课件

这是一份数学九年级上册22.3 实际问题与二次函数备课ppt课件，共15页。PPT课件主要包含了导入课题，学习目标，可得0≤n≤30，可得0≤m≤20，基础巩固，综合应用，拓展延伸等内容，欢迎下载使用。

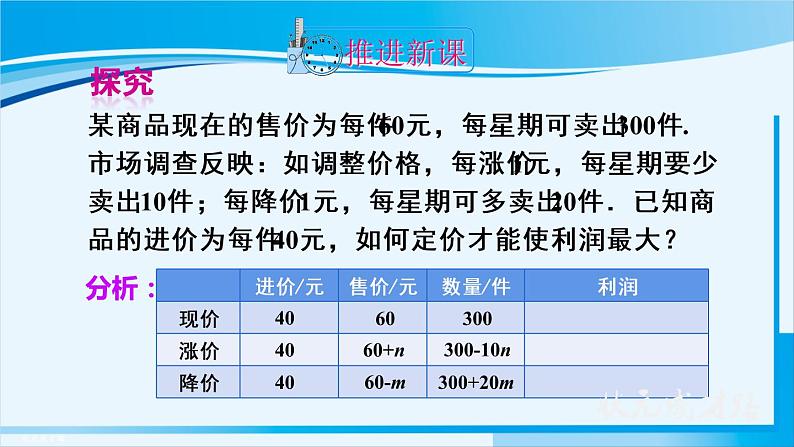
问题：某商品现在的售价为每件60元，每星期可卖出300件.市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，如何定价才能使利润最大？
(1)能用二次函数表示实际问题中的数量关系(包括写出解析式、自变量的取值范围、画图象草图).(2)会用二次函数求销售问题中的最大利润.
某商品现在的售价为每件60元，每星期可卖出300件.市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，如何定价才能使利润最大？
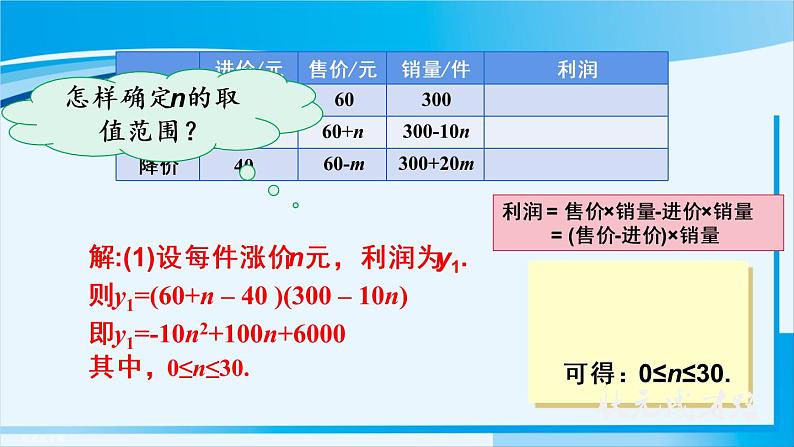
解:(1)设每件涨价n元，利润为y1.则y1=(60+n – 40 )(300 – 10n)即y1=-10n2+100n+6000其中，0≤n≤30.
利润 = 售价×销量-进价×销量 = (售价-进价)×销量
怎样确定n的取值范围？
y1=-10n2+100n+6000 （0≤n≤30）
抛物线y1 =-10n2+100n+6000顶点坐标为 ，所以商品的单价上涨 元时，利润最大，为 元.
n取何值时，y有最大值？最大值是多少？
=-10(n2-10n)+6000
=-10(n-5)2+6250
即涨价情况下，定价65元时，有最大利润6250元.
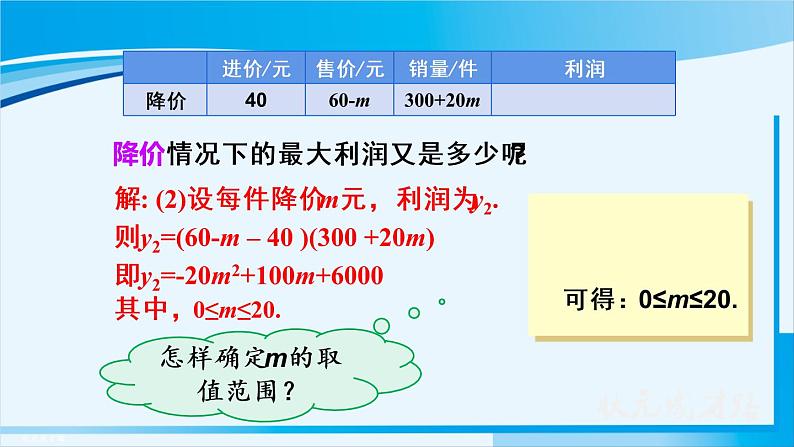
解: (2)设每件降价m元，利润为y2.则y2=(60-m – 40 )(300 +20m)即y2=-20m2+100m+6000其中，0≤m≤20.
怎样确定m的取值范围？
降价情况下的最大利润又是多少呢?
y2=-20m2+100m+6000 (0≤m≤20)
抛物线y2=-20m2+100m+6000顶点坐标为 ，所以商品的单价下降 元时，利润最大，为 元.
m取何值时，y有最大值？最大值是多少？
即降价情况下，定价57.5元时，有最大利润6125元.
=-20(m2-5m)+6000
=-20(m-2.5)2+6125
（2）降价情况下，定价57.5元时，有最大利润6125元.
（1）涨价情况下，定价65元时，有最大利润6250元.
综上可知：该商品的价格定价为65元时，可获得最大利润6250元.
1.下列抛物线有最高点或最低点吗？如果有,写出这些点的坐标(用公式)：(1)y=-4x2+3x; (2)y=3x2+x+6.
2.某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出(200-x)件，应如何定价才能使利润最大？
解：设所得利润为y元,由题意得y=x(200-x)-30(200-x) =-x2+230x-6000 =-(x-115)2+7225 (03.某种文化衫以每件盈利20元的价格出售，每天可售出40件. 若每件降价1元，则每天可多售10件，如果每天要盈利最多，每件应降价多少元？
解：设每件应降价x元，每天的利润为y元，由题意得：y=(20-x)(40+10x) =-10x2+160x+800 =-10(x-8)2+1440 (0＜x＜20).当x=8时，y取最大值1440.即当每件降价8元时，每天的盈利最多。
4.求函数y=-x2+6x+5的最大值和最小值.(1)0≤x≤6； (2) -2≤x≤2.
解：y=-x2+6x+5=-(x-3)2+14(1)当0≤x≤6时，当x=3时， y有最大值14,当x=0或6时，y有最小值5.
(2)当-2≤x≤2时，当x=2时，y有最大值13,当x=-2时，y有最小值-11.
利用二次函数解决利润问题的一般步骤：(1)审清题意，理解问题；(2)分析问题中的变量和常量以及数量之间的关系；(3)列出函数关系式；(4)求解数学问题；(5)求解实际问题.