2021年江苏省徐州市九年级中考数学模拟试卷

2021年江苏省徐州市中考数学模拟试卷

一、选择题（本大题共有8小题，每小题3分，共24分，在每小题所给出的四个选项中，恰有一项是符合要求的，请将正确选项前的字母代号填涂在答题卡相应位置）

1．﹣绝对值是（　　）

A．﹣ B．﹣ C． D．

2．如图是一个机器的零件，则下列说法正确的是（　　）

A．主视图与左视图相同 

B．主视图与俯视图相同 

C．左视图与俯视图相同 

D．主视图、左视图与俯视图均不相同

3．下列计算正确的是（　　）

A．（﹣2a3b）2＝﹣4a6b2 B．（﹣a﹣b）2＝a2﹣2ab+b2 

C．3a•（﹣a）2＝3a3 D．﹣＝

4．如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法用一个长为5m，宽为4m的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计试验结果），他将若干次有效试验的结果绘制成了图②所示的折线统计图，由此他估计不规则图案的面积大约为（　　）

A．6m2 B．7m2 C．8m2 D．9m2

5．某书店与一所山区小学建立帮扶关系，连续6个月向该小学贈送书籍的数量（单位：本）如下：300，200，200，300，300，500，则这组数据的众数、中位数分别是（　　）

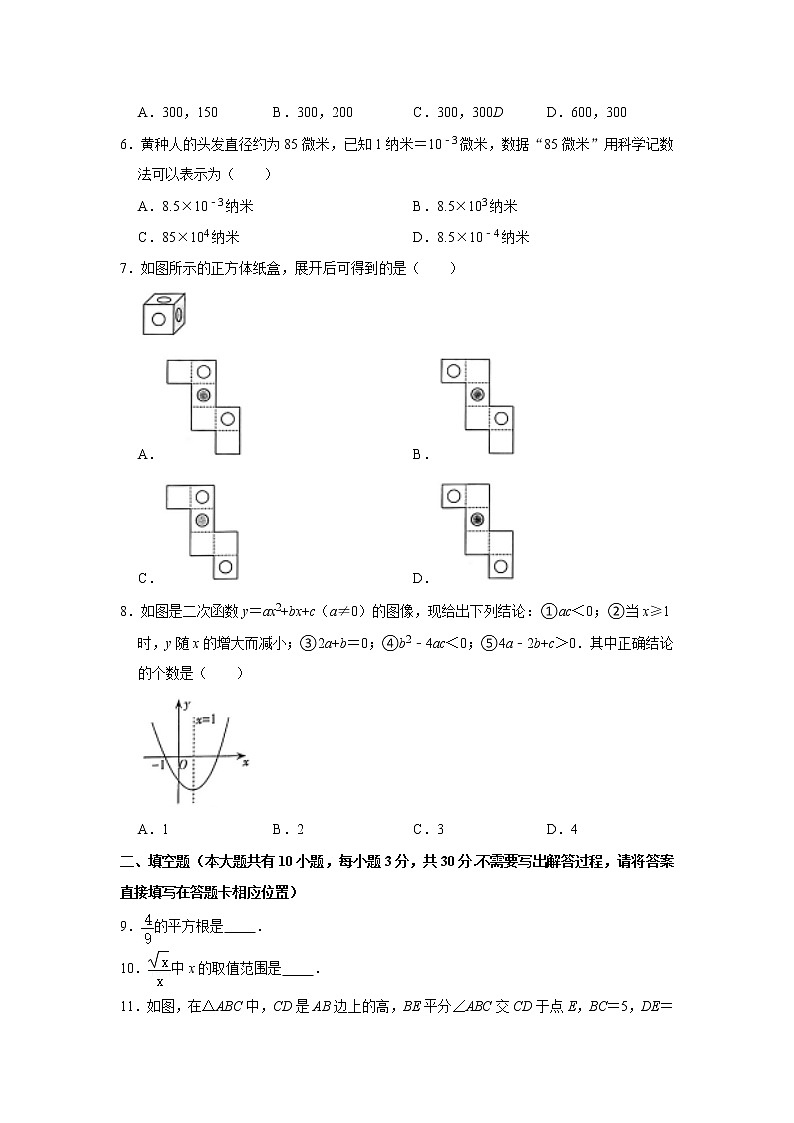
A．300，150 B．300，200 C．300，300D D．600，300

6．黄种人的头发直径约为85微米，已知1纳米＝10﹣3微米，数据“85微米”用科学记数法可以表示为（　　）

A．8.5×10﹣3纳米 B．8.5×103纳米 

C．85×104纳米 D．8.5×10﹣4纳米

7．如图所示的正方体纸盒，展开后可得到的是（　　）

A． B． 

C． D．

8．如图是二次函数y＝ax2+bx+c（a≠0）的图像，现给出下列结论：①ac＜0；②当x≥1时，y随x的增大而减小；③2a+b＝0；④b2﹣4ac＜0；⑤4a﹣2b+c＞0．其中正确结论的个数是（　　）

A．1 B．2 C．3 D．4

二、填空题（本大题共有10小题，每小题3分，共30分.不需要写出解答过程，请将答案直接填写在答题卡相应位置）

9．的平方根是　 　．

10．中x的取值范围是　 　．

11．如图，在△ABC中，CD是AB边上的高，BE平分∠ABC交CD于点E，BC＝5，DE＝2△BCE的面积等于　 　．

12．已知方程组的解也是方程4x﹣3y+k＝0的解，则k的值为　 　．

13．如图，四边形ABCD为⊙O的内接四边形，∠BOD＝110°，则∠BCD的度数是　 　．

14．一个圆锥的底面半径是2cm，母线长是6cm，若将该圆锥侧面沿着母线剪开得到一个扇形，则该扇形的圆心角的度数是　 　．

15．若正比例函数y＝2kx与反比例函数y＝（k≠0）的图像交于点A（m，1），则k的值是　 　．

16．如图，一艘船由A港沿北偏东65°方向航行30km至B港，然后沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，则A，C两港之间的距离为　 　km．

17．如图，以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO，再以BE为对角线作第三个正方形EFBO2，如此作下去，…，则所作的第2021个正方形的面积为　 　．

18．如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，将△ABC绕点B顺时针旋转60得到△BDE，连接AD，则AD的值是　 　．

三、解答题（本大题共有10小题，共86分.请在答题卡指定区域内作答，解答时应写出文宇说明、证明过程或演算步骤）

19．计算：（1）﹣+|tan45°﹣|+（3.14﹣π）°+2﹣2；

（2）﹣

20．（1）解方程：3x（x﹣2）＝x﹣2

（2）解不等式组：

21．为纪念建党100周，某校举行班级歌咏比赛，歌曲有：《十送红军》《映山红》《人民的党》（分别用字母A，B，C依次表示这三首歌曲）．比赛时，将A，B，C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，八（1）班班长先从中随机抽取一张卡片，放回后洗匀，再由八（2）班班长从中随机抽取一张卡片，从而确定歌咏比赛曲目．

（1）八（1）班抽中歌曲《十送红军》的概率是；

（2）试用画树状图或列表的方法求出八（1）班和八（2）班抽中不同歌曲的概率．

22．新学期，某校开设了“防疫宣传”“心理疏导”等课程．为了解学生对新开课程的掌握情况，从八年级学生中随机抽取部分学生进行了一次综合测试测试结果分为四个等级：A级为优秀B级为良好，C级为及格，D级为不及格将测试结果绘制了如下两幅不完整的统计图根据统计图中的信息解答下列问题：

（1）本次抽样测试的学生人数是　 　名；

（2）扇形统计图中表示A级的扇形圆心角的度数是，并把条形统计图补充完整；

（3）该校八年级共有学生500名，如果全部参加这次测试，估计优秀的人数有　 　名．

23．如图，在菱形ABCD中，对角线AC，BD相交于点O，DE∥AC，AE∥BD．

（1）求证：四边形AODE是矩形；

（2）连接CE，若AB＝2，∠BCD＝120°，求CE的长．

24．某社区拟建A，B两类摊位以搞活“地摊经济”，每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的．

（1）求每个A，B类摊位的占地面积各为多少平方米；

（2）该社区拟建A，B两类摊位共90个，且B类摊位的数量不少于A类排位数量的3倍，求最多建多少个A类摊位．

25．如图，AB是⊙O的直径，C是⊙O上一点，P是⊙O外一点，且OP∥BC，∠P＝∠BAC．

（1）求证：PA为⊙O的切线；

（2）如果OP＝AB＝10，求AC的长．

26．工匠制作某种金属工具要进行材料燬烧和锻造两个工序，即需要将材料烧到800℃，然后停止煅烧进行锻造操作，经过8min时，材料温度降为600℃．如图，煅烧时温度y（℃）与时间x（min）成一次函数关系；锻造时，温度y（℃）与时间x（min）成反比例函数关系已知该材料初始温度是32℃．

（1）分别求出材料煅烧和锻造时y与x的函数关系式，并写出自变量x的取值范围；

（2）根据工艺要求，当材料温度低于400℃时，须停止操作，那么锻造的操作时间最多有多长？

（3）如果加工每个零件需要锻造12min，并且当材料温度低于400℃时，需要重新煅烧，通过计算说明加工每个零件，一共需要多长时间？

27．如图①，在矩形ABCD中，AB＝6，BC＝8．把矩形ABCD沿对角线AC剪开，得到△ABC和△ADC，并把△ADC沿线段CB平移得到△A’D’C’，A’C’与AB相交于点N，D’C’与AC相交于点M（如图②）．

（1）四边形AMC’N一定是形；

（2）当四边形AMC’N是菱形时求平移的距离；

（3）如图③，把△ADC沿线段CB平移使DC与AB重合，得到△A’D’C’，再把△A’D’C’绕点B顺时针旋转，使点D’落在边AC上的点D1处，得到△A1D1B，求△FD1B的面积．

28．如图，在平面直角坐标系中，矩形ABCD的三个顶点B（4，0），C（8，0），D（8，﹣8），抛物线y＝ax2+bx经过A，C两点．动点P从点A出发，沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动，运动速度均为每秒1个单位长度，运动时间为t秒，过点P作PE⊥AB交AC于点E．

（1）求点A的坐标及抛物线的函数表达式；

（2）过点E作EF⊥AD于点F，交抛物线于点G．当t为何值时，线段EG的长有最大值？最大值是多少？

（3）连接EQ，是否存在t的值使△ECQ为等腰三角形？若存在，请求出t值若不存在，请说明理由．