

2021年天津市九年级数学中考全真模拟卷(一)(word版 含答案)
展开1.(3分)设[m)表示大于m的最小整数,如[5.5)=6,[﹣1.2)=﹣1,则下列结论中正确的是( )
A.[2)﹣2=0B.若[m)﹣m=0.5,则m=0.5
C.[m)﹣m的最大值是1D.[m)﹣m的最小值是0
2.(3分)计算1﹣2sin245°的结果是( )
A.﹣1B.0C.D.1
3.(3分)据统计,某城市去年接待旅游人数约为89 000 000人,89 000 000这个数据用科学记数法表示为( )
A.8.9×106B.8.9×105C.8.9×107D.8.9×108
4.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
5.(3分)如图所示的几何体的从左面看到的图形为( )
A.B.C.D.
6.(3分)估计的值应在( )
A.7和8之间B.8和9之间C.9和10之间D.10和11之间
7.(3分)若方程组的解中x+y=16,则k等于( )
A.15B.18C.16D.17
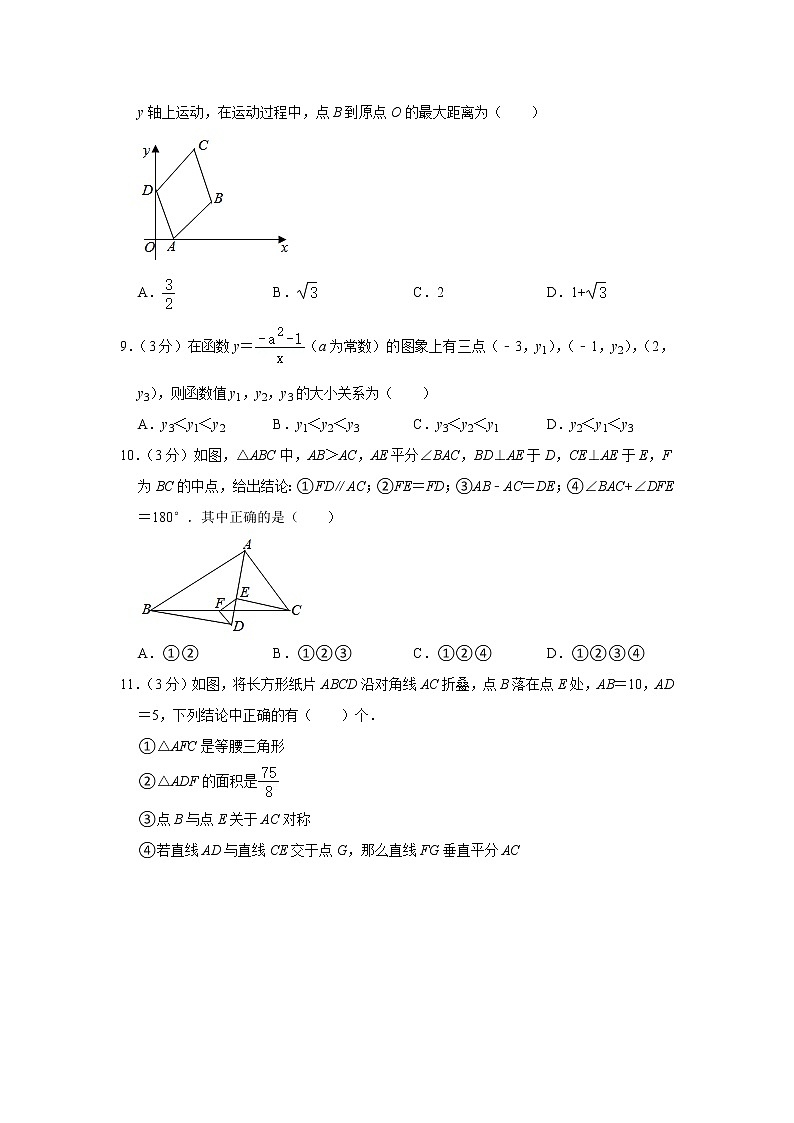
8.(3分)如图,菱形ABCD边长为2,∠C=60°.当点A在x轴上运动时,点D随之在y轴上运动,在运动过程中,点B到原点O的最大距离为( )
A.B.C.2D.1+
9.(3分)在函数y=(a为常数)的图象上有三点(﹣3,y1),(﹣1,y2),(2,y3),则函数值y1,y2,y3的大小关系为( )
A.y3<y1<y2B.y1<y2<y3C.y3<y2<y1D.y2<y1<y3
10.(3分)如图,△ABC中,AB>AC,AE平分∠BAC,BD⊥AE于D,CE⊥AE于E,F为BC的中点,给出结论:①FD∥AC;②FE=FD;③AB﹣AC=DE;④∠BAC+∠DFE=180°.其中正确的是( )
A.①②B.①②③C.①②④D.①②③④
11.(3分)如图,将长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AB=10,AD=5,下列结论中正确的有( )个.
①△AFC是等腰三角形
②△ADF的面积是
③点B与点E关于AC对称
④若直线AD与直线CE交于点G,那么直线FG垂直平分AC
A.1 个B.2 个C.3 个D.4 个
12.(3分)如图,是二次函数y=ax2+bx+c(a≠0)的图象,对称轴为直线x=2,则下列结论正确的有( )个.
①ax2+bx+c=0(a≠0)有两个不相等的实数根
②3a﹣c>0
③a﹣b+c<0
④(0,y1)、(4,y2)在此二次函数的图象上,则y1<y2
A.1B.2C.3D.4
二.填空题(共6小题,满分18分,每小题3分)
13.(3分)若﹣xay﹣2x2yc=bx2y总成立,则abc的值为 .
14.(3分)化简的结果为 .
15.(3分)在一个布袋中装有白球和红球若干个,各个球除颜色外都相同.初二(1)班40名同学做摸球试验,每两人一组,一人从袋中任意摸一个球,另一人记录颜色后将球放回袋中搅匀,每组都做50次这样的摸球试验,然后全班汇总数据.当全班试验中摸出红球的频数为90,根据这个数据,回答下列问题:
(1)全班摸球试验中,共摸出白球 个,摸出红球、白球的频率分别是 和 ;
(2)估计从袋中任意摸1个球,恰好是红球的概率约是 ,恰好是白球的概率约是 ;
(3)由此可估计,袋中红球个数与白球个数之比值约是 ;
(4)若一只袋中共有200个球,可估计袋中红球约有 个,白球约有 个.
16.(3分)直线y=5x﹣6与y轴交点坐标为 .
17.(3分)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动,同时点Q沿边AB,BC从点A开始向点C以2cm/s的速度移动,当点P移动到点A时,P、Q同时停止移动.设点P出发x秒时,△PAQ的面积为ycm2,y与x的函数图象如图②.
则下列四个结论,其中正确的有 .(填序号)
①当点P移动到点A时,点Q移动到点C;
②当AP=AQ时,△PAQ面积达到最大值;
③正方形边长为6cm;
④线段EF所在的直线对应的函数关系式为y=﹣3x+18.
18.(3分)如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,MN的长为 .
三.解答题(共7小题,满分66分)
19.(8分)解不等式组,并把解集表示在数轴上.
(1);
(2).
20.(8分)4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
一、数据收集:从全校随机抽取20名学生,进行每周用于课外阅读时间的调查,数据如下(单位:min):
二、整理数据:按如下分段整理样本数据,得到下面不完全的统计表:
三、分析数据:得到下面不完全的统计表:
四、得出结论:
①上面表格中的数据:a= ,b= ,c= ,d= ;
②这组数据用扇形统计图表示,成绩在40≤x<80范围内的扇形圆心角的大小为 ;
③如果该校现有学生600人,估计等级为“B”的学生有 人;
④假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读 本课外书.
21.(10分)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC交⊙O于点D,E是弧BD的中点,AE与BC交于点F.
(1)求证:∠C=2∠EAB;
(2)已知CD=9,CA=15,求DF的长.
22.(10分)B,D两地间有一段笔直的高速铁路,长度为100km,某时发生的地震对地面上以点A为圆心,30km为半径的圆形区域内的建筑物有影响,分别从B,D两地处测得点A的方位角如图所示,高速铁路是否会受到地震的影响?请通过计算说明理由.(结果精确到0.1km,参考数据:)
23.(10分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
24.(10分)如图①,将▱ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左边),点D坐标为(0,4),直线MN:y=x﹣6沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被▱ABCD截得的线段长度为m,平移时间为t,m与t的函数图象如图②所示.
(1)填空:点C的坐标为 ;在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)
(2)点B的坐标为 ,n= ,a= ;
(3)在平移过程中,求该直线扫过▱ABCD的面积y与t的函数关系式.
25.(10分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于A(﹣1,0),B(3,0)两点,点C为抛物线的顶点.点M(0,m)为y轴上的动点,将抛物线绕点M旋转180°,得到新的抛物线,其中B、C旋转后的对应点分别记为B'、C′.
(1)若原抛物线经过点(﹣2,5),求原抛物线的函数表达式;
(2)在(1)条件下,当四边形BCB'C′的面积为40时,求m的值;
(3)探究a满足什么条件时,存在点M,使得四边形BCB'C′为菱形?请说明理由.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、[2)﹣2=3﹣2=1,故本选项不合题意;
B、若[m)﹣m=0.5,则m不一定等于0.5,故本选项不合题意;
C、[m)﹣m的最大值是1,故本项符合题意;
D、[m)﹣m>0,但是取不到0,故本选项不合题意;
故选:C.
2.解:原式=1﹣2×()2
=1﹣2×
=1﹣1
=0.
故选:B.
3.解:89 000 000这个数据用科学记数法表示为8.9×107.
故选:C.
4.解:A、是轴对称图形,又是中心对称图形,故此选项正确;
B、不是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
5.解:从这个几何体的左面看,所得到的图形是长方形,能看到的轮廓线用实线表示,看不见的轮廓线用虚线表示,
因此,选项D的图形,符合题意,
故选:D.
6.解:∵49<63<64,
∴7<<8,
故选:A.
7.解:由题意得,
①+③得:4x=4k+11④,
①×6+②得:20x=25k﹣30,即4x=5k﹣6⑤,
⑤﹣④得:k=17,
故选:D.
8.解:取AD的中点E,连接BD、EB、EO.如图所示:
∵四边形ABCD是菱形,
∴AD=AB=2,∠BAD=∠C=60°,
∴△ABD是等边三角形,
∵E是AD的中点,
∴BE⊥AD,AE=AD=1,
∴BE=AE=,
在Rt△AOD中,OE为斜边AD上的中线,
∴OE=AD=1,可知OE为定值,
∵圆外一点到圆上一点为最大距离必过圆心,
∴当O、E、B共线时OB最大,其值为OE+BE=+1;
故选:D.
9.解:∵﹣a2﹣1<0,
∴函数y=(a为常数)的图象在二、四象限,且在每一象限内y随x的增大而增大,
∵﹣3<﹣1<0,
∴点(﹣3,y1),(﹣1,y2)在第二象限,
∴y2>y1>0,
∵2>0,
∴点(2,y3)在第四象限,
∴y3<0,
∴y3<y1<y2.
故选:A.
10.解:延长CE交AB于G,延长BD交AC延长线于H,
∵AE平分∠GAC,AE⊥GC,
∴AG=AC,GE=CE,
同理可得,AB=AH,BD=HD,
∵BF=CF,BD=HD,
∴DF∥CH,即DF∥AC,故①正确,
∴DF=CH,
∵GE=CE,BF=CF,
∴EF=BG,
∵GB=AB﹣AG=AH﹣AC=CH,即GB=CH,
∴GB=CH,即EF=DF,故②正确,
∴AB﹣AC=AB﹣AG=BG,
过G作GI⊥BH于I,
∵∠GED=∠EDI=∠GID=90°,
∴四边形GIDE是矩形,
∴GI=ED,
∴BG>GI=ED,
∴AB﹣AC>DE,故③错误;
∵EF∥BG,DF∥HC,
∴∠FED=∠BAD,∠FDE=∠HAD,
∴∠FED+∠FDE=∠BAD+∠HAD=∠BAC,
∵∠FED+∠FDE+∠EFD=180°,
∴∠BAC+∠EFD=180°,故④正确;
故选:C.
11.解:
如图所示:
①∵四边形ABCD为矩形
∴DC∥AB,
∴∠FCA=∠CAB,
由折叠可知:
∠FAC=∠CAB,
∴∠FCA=∠FAC,
∴FA=FC,
∴△AFC是等腰三角形.
∴①正确;
②设DF=x,则FC=FA=10﹣x,AD=5,
∴在Rt△ADF中,x2+52=(10﹣x)2,解得x=,
∴S△ADF=DF•AD=××5=.
∴△ADF的面积为.
∴②正确;
③∵AB=AE,CB=CE,
∴AC是BE的垂直平分线,
∴点B与点E关于AC对称.
∴③正确;
④如图:延长AD和CE交于点G,连接GF,
∵FD=FE,FG=FG,
∴Rt△GDF≌Rt△GEF(HL),
∴GD=GE,又AD=CE,
∴GA=GC,FD=FE,
∴FG是AC的垂直平分线,
∴④正确.
故选:D.
12.解:①从图象看,抛物线与x轴有两个交点,故ax2+bx+c=0(a≠0)有两个不相等的实数根,正确,符合题意;
②抛物线开口向上,则a>0,而c<0,故3a﹣c>0正确,符合题意;
③由图象看,x=﹣1时,y=a﹣b+c>0,故原答案错误,不符合题意;
④函数的对称轴为:x=2,而(0,y1)、(4,y2)与函数对称轴等间隔,故y1=y2,故原答案错误,不符合题意;
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
13.解:因为﹣xay﹣2x2yc=bx2y总成立,
所以a=2,b=﹣1﹣2=﹣3,c=1,
所以abc=2×(﹣3)×1=﹣6.
故答案为:﹣6.
14.解:原式=9﹣8
=1.
故答案为1.
15.解:(1)∵40名同学做摸球试验,每两人一组,一人从袋中任意摸一个球,另一人记录颜色后将球放回袋中搅匀,每组都做50次这样的摸球试验,
∴球的总数为(40÷2)×50=1000个,
∵红球的频数为90,
∴白球的频数为910,
∴摸出红球、白球的频率分别是和;
故答案为;;
(2)∵本次试验次数较多,
∴频率接近于概率,
∴从袋中任意摸1个球,恰好是红球的概率约是,恰好是白球的概率约是;
故答案为;;
(3)∵红球个数为90,白球个数为910,
∴袋中红球个数与白球个数之比值约是9:91;
故答案为9:91;
(4)红球个数为200×=18,
白球个数为200﹣18=182,
故答案为18;182.
16.解:当x=0时,y=5×0﹣6=﹣6,
∴直线y=5x﹣6与y轴交点坐标为(0,﹣6).
故答案为:(0,﹣6).
17.解:①∵点P沿边DA从点D开始向点A以1cm/s的速度移动,
同时点Q沿边AB,BC从点A开始向点C以2cm/s的速度移动,
当点P移动到点A时,P、Q同时停止移动.
当点P移动到点A时,点Q移动到点C.骨①正确;
②根据函数图象可知:
当2AP=AQ时,△PAQ面积达到最大值,故②错误;
③当2AP=AQ时,△PAQ面积达到最大值为9,
设正方形的边长为a(a>0),
则△PAQ面积的最大值=×a×a=9,
解得:a=6,
所以正方形的边长为6cm,故③正确;
④设线段EF所在的直线为y=kx+b,
∵当x=3时,y=9,当x=6时,y=0,
代入y=kx+b中,得:,
解得:,
∴线段EF所在的直线对应的函数关系式为y=﹣3x+18,故④正确;
故答案为:①③④.
18.解:设点P关于OA的对称点为C,关于OB的对称点为D,连接OC,OD,CD,CD分别交OA、OB于点M'、N',连接PM'、PN',如图所示:
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM'=CM',OP=OC,∠COA=∠POA;PN'=DN',OP=OD,∠DOB=∠POB.
∴OC=OD=OP=6,
∵∠AOB=30°,
∴∠COD=∠COA+∠AOP+∠POB+∠BOD
=2∠AOP+2∠POB
=2∠AOB
=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6,
∵OP平分∠AOB,
∴∠POC=∠POD,
∴OP⊥CD,
∴OQ=6sin60°=6×=3,
∴PQ=6﹣3,
设M'Q=x,则PM'=CM'=3﹣x,
∴(3﹣x)2﹣x2=,
解得x=6﹣9.
∴M'N'=2x=12﹣18.
故答案为:12﹣18.
三.解答题(共7小题,满分66分)
19.解:(1)解不等式4x+6>1﹣x,得:x>﹣1,
解不等式3(x﹣1)≤x+5,得:x≤4,
则不等式组的解集为﹣1<x≤4,
将不等式组的解集表示在数轴上如下:
(2)解不等式5x+2≥3(x﹣1),得:x≥﹣2.5,
解不等式1﹣>x﹣2,得:x<0.8,
则不等式组的解集为﹣2.5≤x<0.8,
将不等式组的解集表示在数轴上如下:
20.解:①由已知数据知a=5,b=8;
∵第10、11个数据分别为80、81,
∴中位数c==80.5(min),
∵81出现的次数最多,出现了3次,
∴众数是81min;
故答案为:5,8,80.5,81;
②成绩在40≤x<80范围内的扇形圆心角的大小是:360°×=90°;
故答案为:90°;
③估计等级为“B”的学生有:600×=240(人),
故答案为:240;
④估计该校学生每人一年(按52周计算)平均阅读课外书×52=13(本);
故答案为:13.
21.证明:(1)连接AD,
∵AC是⊙O的切线,AB是直径,
∴∠CAB=90°,
∴∠C+∠ABC=90°,
∵AB是直径,
∴∠ADB=90°,
∴∠DAB+∠ABC=90°,
∴∠C=∠DAB,
∵E是弧BD的中点,
∴=,
∴∠DAE=∠BAE,
∴∠DAB=2∠EAB,
∴∠C=2∠EAB;
(2)∵∠C+∠DAC=90°,∠C+∠ABC=90°,
∴∠DAC=∠ABC,
∴∠DAC+∠DAE=∠ABC+∠BAE,
∴∠CAF=∠CFA,
∴AC=CF=15,
∴DF=CF﹣CD=15﹣9=6.
22.解:如图,过点A作AC⊥BD于点C,
∴∠ACB=∠ACD=90°,
根据题意可知:∠ABC=45°,∠ADC=30°,
∴∠BAC=45°,
∴BC=AC,
在Rt△ACD中,tan∠ADC=,
∴CD==AC,
∵BD=BC+CD,
∴AC+AC=100,
解得AC=50(﹣1)≈36.6>30,
∴高速铁路不会受到地震的影响.
23.解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
24.解:(1)令y=0,则x﹣6=0,解得x=8,
令x=0,则y=﹣6,
∴点M(8,0),N(0,﹣6)
∴OM=8,ON=6,
由图2可知5秒后直线经过点C,
∴CM=5,OC=OM﹣CM=8﹣5=3,
∴C(3,0),
∵10秒~a秒被截线段长度不变,
∴先经过点B;
故填:(3,0);B
(2)由图2可知BM=10,
∴OB=BM﹣OM=10﹣8=2,
∴B(﹣2,0),
在Rt△OCD中,由勾股定理得,CD==5,
∴BC=CD=5,
∴▱ABCD是菱形,
∵,
∴MN⊥CD,
∴n=DO=4
∵设直线MN向x轴负方向平移的速度为每秒1个单位的长度,
平移后的直线解析式为y= (x+t)﹣6,
把点D(0,4)代入得,(0+t)﹣6=4,
解得t=,
∴a=;
故答案为:(1)(3,0),B;(2)(﹣2,0),4,;
(3)当0≤t≤5时,y=0;
当5<t≤10,如图1,该直线与BC、CD分别交于F、E,FC=t﹣5,
∵直线CD的解析式为:y=﹣x+4,
∴EF⊥CD,
∴△CEF∽△COD,
∴,
∴,
∴EF=,CE=,
∴y=××==t2﹣t+6,
当10<t≤,如图2,直线与AB、CD分别交于G、E,与射线CB交于F,FB=t﹣10,
∵△BGF∽△COD,
∴
∴FG=,BG=,
y=S△CEF﹣S△BGF=﹣=(10t﹣75)=t﹣18,
当时,如图3,BG=,AG=5﹣,
∵△EAG∽△DCO,
∵=,
∴DG=×(5﹣),
∴y=20﹣(5﹣)××(5﹣)=﹣+t﹣,
当t≥时y=20.
综上所述:
y=.
25.解:(1)由题意得:,
解得,
∴原抛物线的函数表达式为:y=x2﹣2x﹣3;
(2)连接CC′、BB′,延长BC,与y轴交于点E,
∵二次函数y=x2﹣2x﹣3的顶点为(1,﹣4),
∴C(1,﹣4),
∵B(3,0),
∴直线BC的解析式为:y=2x﹣6.
∴E(0,﹣6),
∵抛物线绕点M旋转180°,
∴MB=MB′,MC=MC′,
∴四边形BCB′C′是平行四边形,
∴S△BCM=×40=10,
∵S△BCM=S△MBE﹣S△MCE=×(3﹣1)×ME=ME,
∴ME=10,
∴m=4或m=﹣16;
(3)如图,过点C作CD⊥y轴于点D,
当平行四边形BCB'C′为菱形时,应有MB⊥MC,故点M在O、D之间,
当MB⊥MC时,△MOB∽△CDM,
∴=,
即MO•MD=BO•CD.
∵二次函数y=a(x+1)(x﹣3)的顶点为(1,﹣4a),M(0,m),B(3,0),
∴CD=1,MO=﹣m,MD=m+4a,OB=3,
∴﹣m(m+4a)=3,
∴m2+4am+3=0,
∵△=16a2﹣12≥0,a>0,
∴a≥.
所以a≥时,存在点M,使得四边形BCB'C′为菱形.30
60
81
50
44
110
130
146
80
100
60
80
120
140
75
81
10
30
81
92
课外阅读时间x(min)
0≤x<40
40≤x<80
80≤x<120
120≤x<160
等级
D
C
B
A
人数
3
a
b
4
平均数
中位数
众数
80
c
d
2021年北京市九年级数学中考全真模拟卷(一)(word版 含答案): 这是一份2021年北京市九年级数学中考全真模拟卷(一)(word版 含答案),共21页。
2021年北京市九年级数学中考全真模拟卷(二)(word版 含答案): 这是一份2021年北京市九年级数学中考全真模拟卷(二)(word版 含答案),共21页。
2021年北京市九年级数学中考全真模拟卷(五)(word版 含答案): 这是一份2021年北京市九年级数学中考全真模拟卷(五)(word版 含答案),共21页。












