_山东省日照市专用 2021年备考中考押题卷（word版 含答案）

日照市2021年备考中考押题卷

一、选择题:本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合要求的，请把符合要求的的选项选出来.

1．(本题3分)下列计算正确的是(       )

A．-|-2|=2 B．-12=-1 C．（-2）2=-4 D．33=9

2．(本题3分)下列图形是公共设施标志，其中是轴对称图形的是(    )

A． B． C． D．

3．(本题3分)下列计算正确的是（ ）

A． B． C． D．

4．(本题3分)某桑蚕丝的直径用科学记数法表示为1.6×10-5米，则这个数的原数是

A．0.0000016 B．0.000016 C．0.00016 D．0.0016

5．(本题3分)一元二次方程x2－5x＋6＝0的两根分别是x1、x2，则x1＋x2等于( )

A．5 B．6 C．－5 D．－6

6．(本题3分)如图，正方体展开图的每个面上都有一个汉字，那么在原正方体的表面上，与“一”相对面上的汉字是（    ）

A．态 B．度 C．决 D．定

7．(本题3分)如图，OA在x轴上，OB在y轴上，OA＝4，OB＝3，点C在边OA上，AC＝1，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切．若反比例函数y＝（k≠0）的图象经过圆心P，则k的值是（　　）

A． B． C． D．﹣2

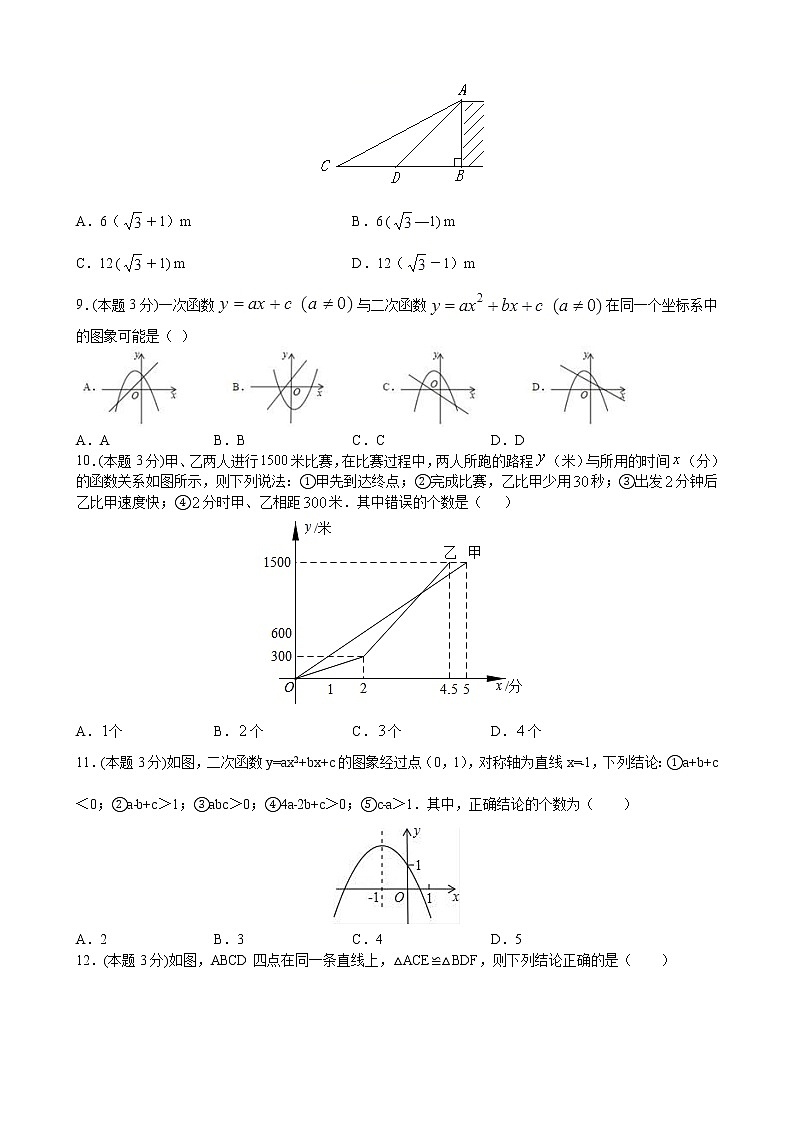
8．(本题3分)如图为了测量某建筑物AB的高度，在平地上C处测得建筑物顶端A的仰角为30°，沿CB方向前进12 m到达D处，在D处测得建筑物顶端A的仰角为45°，则建筑物AB的高度等于（ ）

A．6（＋1）m B．6 (—1) m

C．12 (＋1) m D．12（－1）m

9．(本题3分)一次函数与二次函数在同一个坐标系中的图象可能是（ ）

A．A B．B C．C D．D

10．(本题3分)甲、乙两人进行米比赛，在比赛过程中，两人所跑的路程（米）与所用的时间（分）的函数关系如图所示，则下列说法：①甲先到达终点；②完成比赛，乙比甲少用秒；③出发分钟后乙比甲速度快；④分时甲、乙相距米．其中错误的个数是（ 　）

A．个 B．个 C．个 D．个

11．(本题3分)如图，二次函数y=ax2+bx+c的图象经过点（0，1），对称轴为直线x=﹣1，下列结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④4a﹣2b+c＞0；⑤c﹣a＞1．其中，正确结论的个数为（　　）

A．2 B．3 C．4 D．5

12．(本题3分)如图，ABCD四点在同一条直线上，△ACE≌△BDF，则下列结论正确的是（　　）

A．△ACE和△BDF成轴对称

B．△ACE经过旋转可以和△BDF重合

C．△ACE和△BDF成中心对称

D．△ACE经过平移可以和△BDF重合

二、填空题:本大题共4小题，每小题4分，共16分.不需写解答过程，只要求填写最后结果.

13．(本题4分)分解因式__________________．

14．(本题4分)已知圆锥的母线长是5，侧面积是15π则这个圆锥的半径是_________．

15．(本题4分)如图，△ABC中，∠BAC＝90°，∠B＝30°，BC边上有一点P（不与点B，C重合），I为△APC的内心，若∠AIC的取值范围为m°＜∠AIC＜n°，则m+n＝_____．

16．(本题4分)如图，△OAB是等边三角形，且OA与x轴重合，点B是反比例函数y＝﹣图象上的点，则△OAB的周长为_____．

三、解答题:本大题共6小题，共68分．解答要写出必要的文字说明、证明过程或演算步骤.

17．(本题10分)（1）计算：．

（2）解方程：．

18．(本题10分)随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位及养老建筑不断增加．

（1）该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个，求该市这两年（从2017年底到2019年底）拥有的养老床位数的平均年增长率；

（2）该市某社区今年准备新建一养老中心，如果计划赡养200名老人，建筑投入平均5万元/人，且计划赡养的老人每增加5人，建筑投入平均减少1000元/人，那么新建该养老中心需申报的最高建筑投入是多少？

19．(本题10分)下表是某班21名学生的第一次数学测验成绩分配表：

若成绩的平均数为70分，

（1）求x和y的值．

（2）求中位数

20．(本题10分)如图，△ABC内接于⊙O，AB＝AC，过点A作AD⊥AB交⊙O于点D，交BC于点E,点F在DA的延长线上，且∠ABF＝∠C ．

（1）求证：BF是⊙O的切线；

（2）若AD＝4，cos∠ABF=，求BC的长．

21．(本题14分)今年．某电动车商场为适应电动车进电梯的需求，需要购进100辆某型号的小型电动车供客户作宣传，经调查，该小型电动车2015年单价为2000元，2017年单价为1620元．

（1）求2015年到2017年该小型电动车单价平均每年降低的百分率；

（2）选购期间发现该小型电动车在A，B两个厂家有不同的促销方案，A厂家买十送一，B厂家全场打九折，试问去哪个厂家买更优惠？

22．(本题14分)已知二次函数y=a（x-m）2-a（x-m）（a，m为常数，且a≠0）．

（1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；

（2）设该函数的图象与x轴的两个交点为A（x1，0），B（x2，0），且x12+x22=25，求m的值；

（3）设该函数的图象的顶点为C，与x轴交于A，B两点，且△ABC的面积为1，求a的值．

参考答案

1．B

【解析】∵-|-2|=-2，∴A错误；

∵-12=-1，∴B正确;

∵（-2）2=4，∴C错误；

∵33=27，∴D错误；

故选B.

2．C

【解析】在平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形是轴对称图形，由此判断A、B、D均不符合轴对称图形的定义.选项C符合轴对称图形的定义.

故选C.

3．C

【解析】A. ∵ 与不是同类项，不能合并，故不正确； 

B. ，故不正确；    

C. ，故正确；    

D. ，故不正确；

故选C.

4．B

【解析】根据科学记数法的定义1.6×10﹣5=0.000016.

故选 B

5．A

【解析】解：∵一元二次方程x2-5x+6=0的两根分别是x1，x2，

故选A．

6．A

【解析】解：正方形的表面展开图，相对的面之间一定相隔一个正方形，

“度”和“定”是相对面；“态”和“一”是相对面；“决“和“切”是相对面.

故选A.

7．A

【解析】解：作PM⊥AB于M，PN⊥x轴于N，如图，设⊙P的半径为r，

∵⊙P与边AB，AO都相切，

∴PM＝PN＝r，

∵OA＝4，OB＝3，AC＝1，

∴AB＝5，

∵S△PAB+S△PAC＝S△ABC，

∴•5r+•r•1＝•3•1，解得r＝，

∴BN＝，

∵OB＝OC，

∴△OBC为等腰直角三角形，

∴∠OCB＝45°，

∴NC＝NB＝，

∴ON＝3﹣＝，

∴P点坐标为（，﹣），

把P（，﹣）代入y＝得k＝×（﹣）＝﹣．

故选A．

8．A

【解析】根据题意可得：BC=

∴AB=6（+1）．

故选A．

9．D

【解析】当x＝0时，都有y＝c，所以，一次函数与二次函数都过点（0，c），排除A；对于B，由直线知a<0，由二次函数知a＞0，矛盾；对于C，由直线知a＞0，由二次函数图象知a＜0，矛盾，只有D符合．

10．A

【解析】由函数图象可以得出乙运动员先到达终点，故说法①错误；
完成比赛，乙比甲少用的时间为：5-4.5=0.5分=30秒，故说法②正确；
由函数图象可以得出出发2分钟后乙比甲速度快，故说法③正确；
由函数图象可以得出2分时甲、乙相距300米，故说法④正确．
综上所述，错误的说法有①共1个．
故选：A．

11．D

【解析】解：①由图象可知：x=1时，y＜0，

∴y=a+b+c＜0，故①正确；

②由图象可知x=﹣1时，y＞1，

∴y=a﹣b+c＞1，故②正确；

③由图象可知： 

∴ab＞0，

又∵c=1，

∴abc＞0，故③正确；

④由图象可知：（0，0）关于x=﹣1对称点为（﹣2，0）

∴令x=﹣2，y＞0，

∴4a﹣2b+c＞0，故④正确；

⑤由图象可知：a＜0，c=1，

∴c﹣a=1﹣a＞1，故⑤正确；

故选D．

12．D

【解析】解：∵△ACE≌△BDF，

∴∠A=∠FBD，∠ECA=∠D，AC=BD，

∴AE∥BF，EC∥DF，

∴△ACE经过平移可以得到△BDF，

故选：D．

13．

【解析】解：原式=x（y-3）-2（y-3）
=（y-3）（x-2）

故答案为：（y-3）（x-2）

14．3

【解析】解：设底面半径为R，则底面周长=2πR，

∴侧面积=，

∴R=3．

故答案为：3．

15．255．

【解析】解：设∠BAP＝α，则∠APC＝α+30°，

∵∠BAC＝90°，

∴∠PCA＝60°，∠PAC＝90°﹣α，

∵I为△APC的内心，

∴AI、CI分别平分∠PAC，∠PCA，

∴∠IAC＝∠PAC，∠ICA＝∠PCA，

∴∠AIC＝180°﹣（∠IAC+∠ICA）

＝180°﹣（∠PAC+∠PCA）

＝180°﹣（90°﹣α+60°）

＝α+105°

∵0＜α＜90°，

∴105°＜α+105°＜150°，即105°＜∠AIC＜150°，

∴m＝105，n＝150．

∴m+n＝255，

故答案为：255．

16．12

【解析】如图，设△OAB的边长为a，过B点作BM⊥x轴于点M．

又∵△OAB是等边三角形，

∴OM＝OA＝a，BM＝，

∴点B的坐标为（﹣a，a），

∵点B是反比例函数y＝﹣图象上的点，

∴﹣a•a＝﹣4，

解得a＝±4（负值舍去），

∴△OAB的周长为：4×3＝12．

故答案为12．

17．（1）3；（2），

【解析】解：（1）原式，

，

；

（2），

，

则或，

解得，．

18．（1）平均年增长率为20%；（2）最高建筑投入为10125000元

【解析】解：（1）设平均年增长率为，

根据题意得，，

解得或（舍去）．

答：平均年增长率为20%．

（2）设在200人的基础上增加人时，建筑总投入为元，

则，

故当时，有最大值，为10125000．

答：最高建筑投入为10125000元．

19．（1）；（2）70

【解析】（1）依题意得，

解得；

（2）∵21÷2＝10.5，而1＋4＋12＝16，

∴中位数为70．

20．（1）证明见解析；（2）

【解析】（1）证明：如图，连接BD

∵AD⊥AB，

∴DB是⊙O的直径，

∴∠D+∠ABD=90°，

又∵∠D=∠C，∠ABF=∠C，

∴∠ABD+∠ABF=90°，

∴OB⊥BF，

∴BF是⊙O的切线；

（2）如图，连接OA，交BC于点G，

∵AC=AB，

∴弧AC=弧AB

∴∠D=∠2=∠ABF，OA⊥BC，BG=CG，

∴cos∠D=cos∠2=cos∠ABF=，

在△ABD中，∠DAB=90°，

∴BD==5，

∴AB==3，

在△ABG中，∠AGB=90°，AD=4，

∴BG=AB×cos∠2=，

∴BC=2BG=．

21．（1）2015年到2017年该小型电动车单价平均每年降低的百分率为10%；（2）去B厂家购买电动车更优惠．

【解析】（1）设2015年到2017年该小型电动车单价平均每年降低的百分率为x，根据题意得：

2000×（1﹣x）2=1620

解得：x=0.1=10%，或x=1.9（舍去）．

答：2015年到2017年该小型电动车单价平均每年降低的百分率为10%．

（2）100×=≈90.91（辆），在A厂家需要的费用为1620×91=147420（元），在B厂家需要的费用为1620×100×0.9=145800（元）．

而147420＞145800，故去B厂家购买电动车更优惠．

22．（1）证明见解析；（2）m的值为-4或3；（3）a的值是±8．

【解析】（1）证明：令y=0，a（x-m）2-a（x-m）=0，

△=（-a）2-4a×0=a2，

∵a≠0，

∴a2＞0，

∴不论a与m为何值，该函数的图象与x轴总有两个公共点；

（2）解：y=0，则a（x-m）2-a（x-m）=a（x-m）（x-m-1）=0，

解得x1=m，x2=m+1，

∵x12+x22=25，

∴m2+（m+1）2=25，

解得m1=-4，m2=3．

故m的值为-4或3；

（3）解：∵x1=m，x2=m+1，

∴AB=（m+1）-m=1，

y=a（x-m）2-a（x-m）=a（x-m-）2-，

△ABC的面积=×1×|-|=1，

解得a=±8．

故a的值是±8．