1.1集合的概念及表示方法

这是一份1.1集合的概念及表示方法，文件包含第1课迎接蚕宝宝的到来pptx、第1课迎接蚕宝宝的到来docx、为蚕建造一个家mp4、蚕的孵化mp4、观察蚕卵的样子mp4等5份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

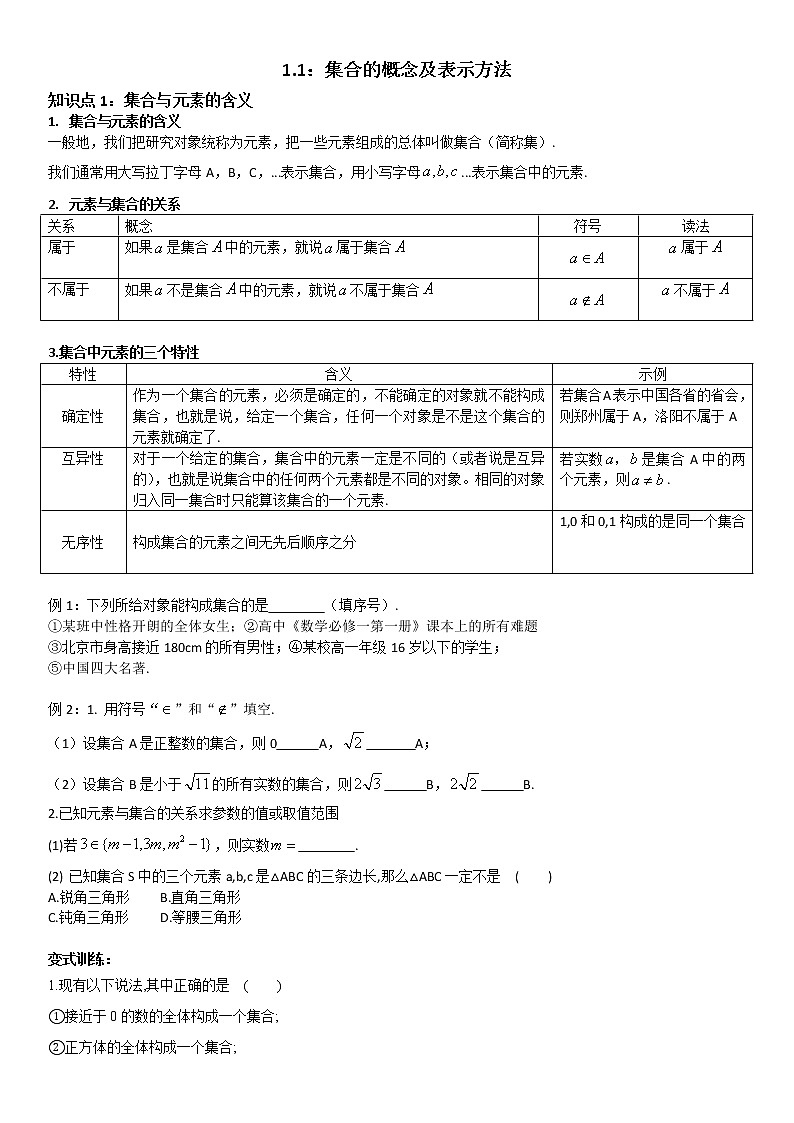
集合与元素的含义
一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合（简称集）.
我们通常用大写拉丁字母A，B，C，...表示集合，用小写字母...表示集合中的元素.
元素与集合的关系
3.集合中元素的三个特性
例1：下列所给对象能构成集合的是 （填序号）.
①某班中性格开朗的全体女生；②高中《数学必修一第一册》课本上的所有难题
③北京市身高接近180cm的所有男性；④某校高一年级16岁以下的学生；
⑤中国四大名著.
例2：1. 用符号“”和“”填空.
设集合A是正整数的集合，则0 A， A；
设集合B是小于的所有实数的集合，则 B， B.
2.已知元素与集合的关系求参数的值或取值范围
(1)若，则实数 .
已知集合S中的三个元素a,b,c是△ABC的三条边长,那么△ABC一定不是 ( )
A.锐角三角形B.直角三角形
C.钝角三角形D.等腰三角形
变式训练：
1.现有以下说法,其中正确的是 ( )
①接近于0的数的全体构成一个集合;
②正方体的全体构成一个集合;
③未来世界的高科技产品构成一个集合;
④不大于3的所有自然数构成一个集合.
A.①② B.②③ C.③④ D.②④
2.已知集合A仅含有三个元素2,4,6,且当a∈A时,6-a∈A,那么a的值为 ( )
A.2 B.2或4 C.4D.6
3.设集合，集合，已知且，则实数的值为 .
4.已知集合A中含有两个元素，若-3A，则实数的值为 .
5.设集合A=则（ ） A. B. C. D.
6.由实数x, -x, |x| ,, -所组成的集合最多含 ( )
A.2个元素B.3个元素 C.4个元素D.5个元素
4.集合相等
根据集合中元素的无序性，我们可以判断两个集合是否相等：只要构成两个集合的元素是一样的，我们就称这两个集合是相等的.集合A与集合B相等记作A=B.
例1：集合A中含有两个元素和，集合B中含有两个元素0和，若A，B相等，则实数的值为 ，实数的值为 .
变式训练：
1：（2020·山东省泰安市名校联考）设若集合则= .
集合的分类
空集：不含任何元素的集合称为空集，记为
知识点二：集合的表示方法
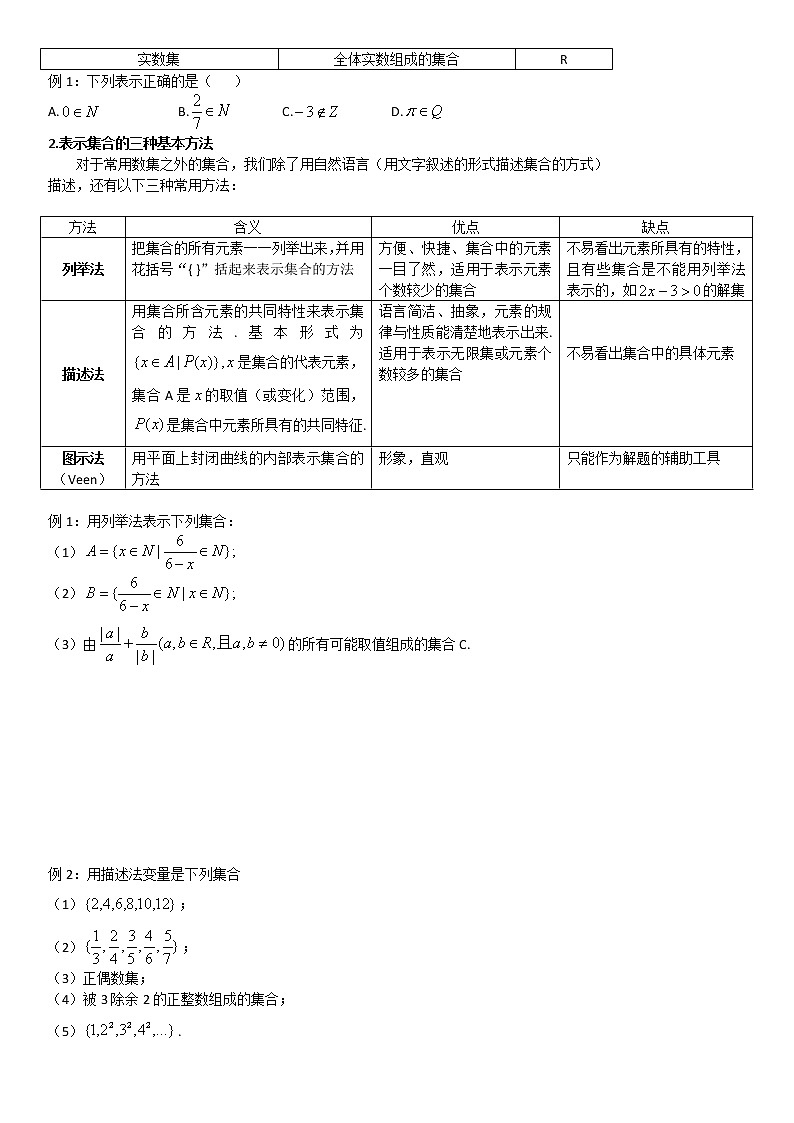
1.常用数集及其记法
例1：下列表示正确的是（ ）
A. B. C. D.
2.表示集合的三种基本方法
对于常用数集之外的集合，我们除了用自然语言（用文字叙述的形式描述集合的方式）
描述，还有以下三种常用方法：
例1：用列举法表示下列集合：
由的所有可能取值组成的集合C.
例2：用描述法变量是下列集合
；
；
正偶数集；
被3除余2的正整数组成的集合；
.
变式训练：
1：用适当的方法表示下列集合
方程组的解集；
所有小于13的既是奇数又是素数的自然数组成的集合；
方程的实数根组成的集合；
平面直角坐标系内所有第二象限的点组成的集合；
二次函数的图像上所有的点组成的集合；
二次函数的图像上所有点的纵坐标组成的集合；
知识点3：数集和点集与集合与方程
集合的元素类型以数、点、图形或方程等形式出现，对于已知集合必须弄清集合元素的形式，特别是对于用描述法给定的集合，要弄清楚它的代表元素是什么，代表元素有何属性.
题型一：区分并判断点集与数集

题型2：集合与方程的综合问题
例1：（江西高考题）若集合中只有一个元素，则（ ）.
4 B. 2 C. 0 D. 0或4
变式训练：
1：若集合中至多有一个元素，则实数的取值范围 （用集合表示）
2：满足，且关于的方程有实数解的有序数对的个数为（ ）
14 B. 13 C. 12 D. 10
3：设，若，试用列举法表示集合B.
题型3： 集合新定义题
例1：定义集合运算：；设，则集合中元素的个数为（ ）
0 B. 2 C.3 D.6
例2: 设P、Q为两个非空数集，定义集合，若，则P+Q中元素的个数是（ ）.
A.9 B. 8 C.7 D. 6
变式训练：
1:（新课标全国卷）已知集合，则B中所含元素的个数为（ ）.
A.3 B. 6 C.8 D. 10
2：（福建高考题改编）在正数集Z中，被5除所得余数为的所有整数组成一个“类”，记为[]，即[]=，给出如下四个结论：
①；②；③若整数属于同一“类”，则④若，则整数属于同一“类”.
其中，正确结论的个数是（ ）
1 B. 2 C. 3 D.4
基础巩固
1.（多选题）下列各组对象能构成集合的有（ ）
A.接近于0的实数 B.小于0的实数
C.（2020,1）与（1,2020） D.1，2，3，1
2.下列集合中与{2,3}是同一集合的是（ ）
A.{{2}，{3}} B.{（2,3）} C.{（3,2）} D.{3,2}
3.已知，且，则的值为（ ）
A. 0 B. 1 C. 2 D.3
4.已知集合中的三个元素是△ABC的三边长，那么三角形ABC一定不是（ ）
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
5.下列结合中恰有两个元素的是（ ）
A. B.
C. D.
6.已知集合，其中.若1是集合A中的一个元素，则集合（ ）
A. B. C. D.
7.已知集合，则A可用列举法表示为 .
8.已知，若，则实数的值为 .
9.用适当的方法表示下列集合：
（1）一年中有31天的月份的全体；
（2）大于-3.5小于12.8的整数的全体；
（3）梯形的全体构成的集合；
（4）所有能被3整除的集合；
（5）方程的解集；
（6）不等式的解集.
综合提升：
10.已知集合，若A=B，则（ ）.
A. 1 B. 2 C. -1 D. -2
11.若集合则集合中元素的个数为（ ）.
A. 5 B. 4 C. 3 D. 2
12.已知为非零实数，则集合为（ ）.
A. B. C. D.
13.若集合，且，则有（ ）
A. B.
C. D.不属于中的任意一个
14.对于任意两个正整数，定义某种运算：当都为偶数或奇数时，；当中一个为奇数，另一个为偶数时，在上述定义下，集合中元素的个数为（ ）
A.48 B.41 C.40 D.39
15.已知集合A中的元素均为整数，对于，如果，那么称是A的一个“孤立元”.给定集合，由S中的3个元素构成的所有集合中，不含“孤立元”的集合共有 个.
16.已知，若A中有且只有一个元素，求的值，并求出这个集合.
参考答案
BCD
D
D
D
C
C
{-1,2,3,4}
1
（1）{1月，3月，5月，7月，8月，10月，12月}
（2）{-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11,12}
（3）{x|x是梯形}或{梯形}
（4）
（5）{1,2}
（6）
10.B
11.C
12.C
13.B
14.B
15. 6
16.时，；时，.
关系
概念
符号
读法
属于
如果是集合中的元素，就说属于集合
属于
不属于
如果不是集合中的元素，就说不属于集合
不属于
特性
含义
示例
确定性
作为一个集合的元素，必须是确定的，不能确定的对象就不能构成集合，也就是说，给定一个集合，任何一个对象是不是这个集合的元素就确定了.
若集合A表示中国各省的省会，则郑州属于A，洛阳不属于A
互异性
对于一个给定的集合，集合中的元素一定是不同的（或者说是互异的），也就是说集合中的任何两个元素都是不同的对象。相同的对象归入同一集合时只能算该集合的一个元素.
若实数是集合A中的两个元素，则.
无序性
构成集合的元素之间无先后顺序之分
1,0和0,1构成的是同一个集合
数集
意义
符号
非负整数集（或自然数集）
全体非负整数组成的集合
N
正整数
全体正整数组成的集合
N或N
整数集
全体整数组成的集合
Z
有理数集
全体有理数组成的集合
Q
实数集
全体实数组成的集合
R
方法
含义
优点
缺点
列举法
把集合的所有元素一一列举出来，并用花括号“{ }”括起来表示集合的方法
方便、快捷、集合中的元素一目了然，适用于表示元素个数较少的集合
不易看出元素所具有的特性，且有些集合是不能用列举法表示的，如的解集
描述法
用集合所含元素的共同特性来表示集合的方法.基本形式为是集合的代表元素，集合A是的取值（或变化）范围，是集合中元素所具有的共同特征.
语言简洁、抽象，元素的规律与性质能清楚地表示出来.适用于表示无限集或元素个数较多的集合
不易看出集合中的具体元素
图示法（Veen）
用平面上封闭曲线的内部表示集合的方法
形象，直观
只能作为解题的辅助工具