八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形课前预习ppt课件

这是一份八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形课前预习ppt课件，共15页。PPT课件主要包含了课件说明，∴ACBD，课堂小结等内容，欢迎下载使用。

本课是在学习菱形概念及性质的基础上，通过类比　平行四边形和矩形的判定定理的探究过程，探索和　证明菱形的两个判定定理．
学习目标：　1．掌握菱形的三种判定方法，能根据不同的已知条　　 件，选择适当的判定定理进行推理和计算；　2．经历菱形判定定理的探究过程，渗透类比思想， 体会研究图形判定的一般思路．学习重点： 菱形判定条件的探索、证明和应用．
回顾反思 类比猜想
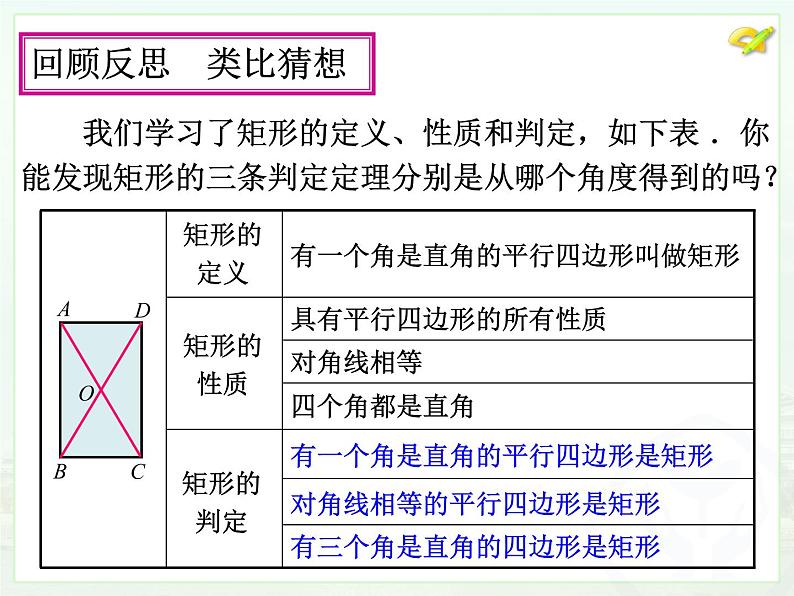
　　我们学习了矩形的定义、性质和判定，如下表 ．你能发现矩形的三条判定定理分别是从哪个角度得到的吗？
有一个角是直角的平行四边形叫做矩形
具有平行四边形的所有性质
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
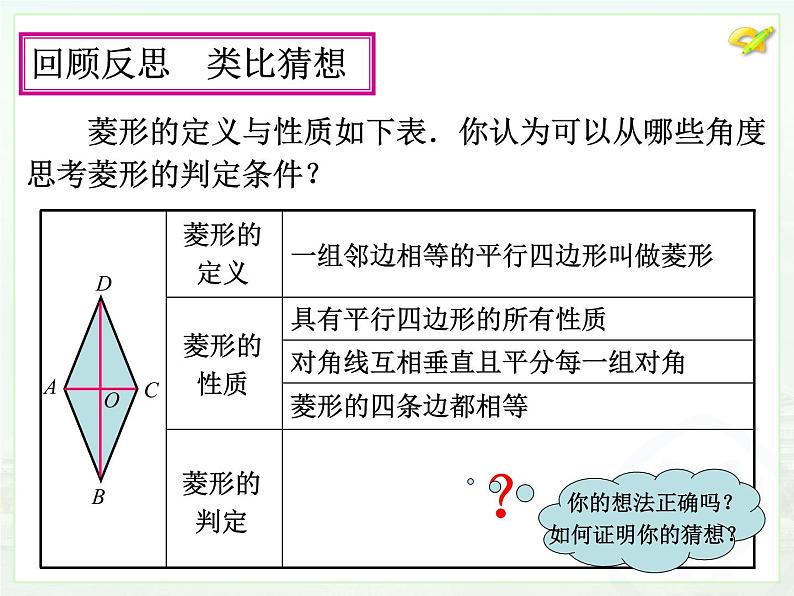
　　菱形的定义与性质如下表．你认为可以从哪些角度思考菱形的判定条件？
一组邻边相等的平行四边形叫做菱形　
对角线互相垂直且平分每一组对角　
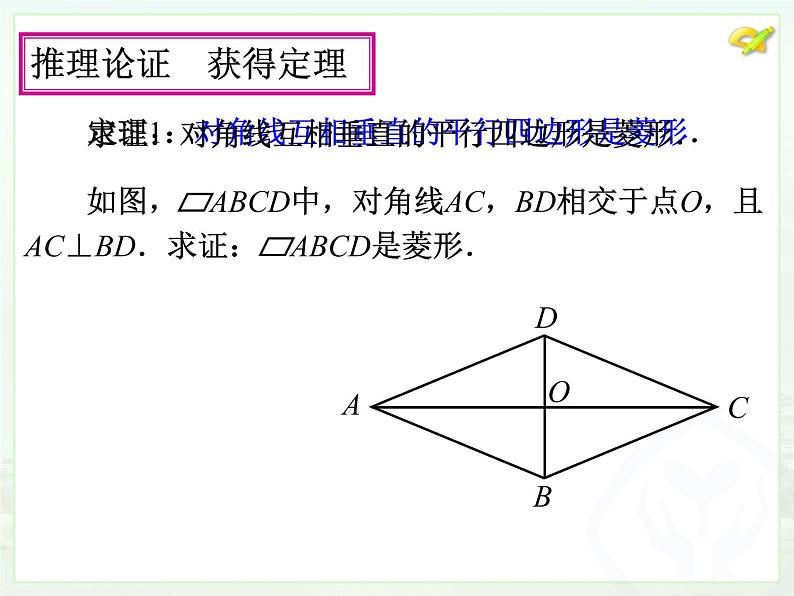
　　定理1：对角线互相垂直的平行四边形是菱形．
推理论证　获得定理　
　　求证：对角线互相垂直的平行四边形是菱形．　　　
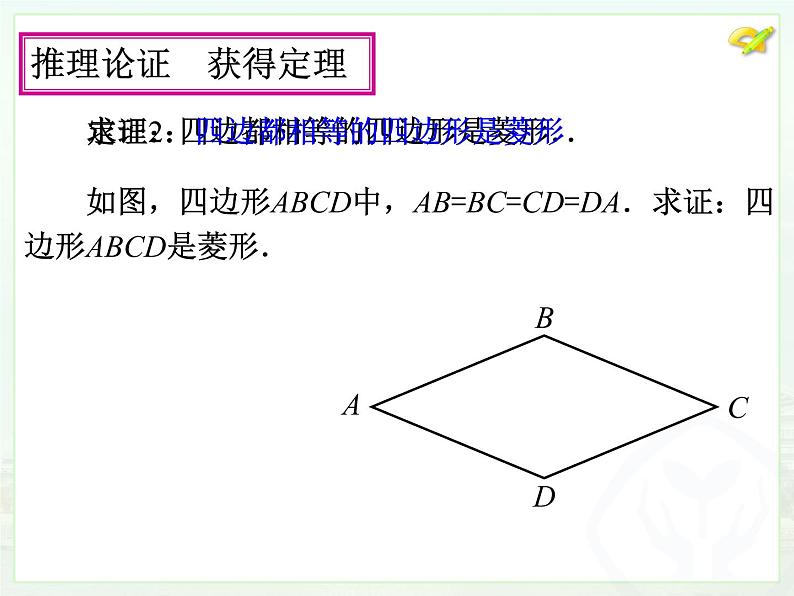
　　求证：四边都相等的四边形是菱形．　　　
　　如图，四边形ABCD中，AB=BC=CD=DA．求证：四边形ABCD是菱形．
　　定理2：四边都相等的四边形是菱形．
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
应用练习 巩固知识 　
　　如图，用一长一短两根木条，在它们的中点处固定一个小钉，做成一个可转动的十字，四周围上一根橡皮　筋，做成一个四边形．转动木条，这个四边形什么时候变成菱形？请说明理由．
　　如图，先画两条等长的线段AB，AD，然后分别以B，D为圆心，AB长为半径画弧，两弧交点为C，连接BC，CD．得到的四边形ABCD是菱形吗？请说明理由．
∴四边形ABCD是菱形.
∴OA=OC=4 OB=OD=3
又∵ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
∴AB2=AO2+BO2
如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边形EFGH是菱形。
∵四边形ABCD是矩形
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
综合运用　发展能力 　
　　如图，AD平分∠BAC，DE∥AC交AB于点E，DF∥AB交AC于点F．求证：四边形AEDF是菱形．
一组对边平行且相等两组对边分别相等　
两组对角分别相等对角线互相平分