初中数学人教版八年级下册17.1 勾股定理图文课件ppt

这是一份初中数学人教版八年级下册17.1 勾股定理图文课件ppt，共25页。PPT课件主要包含了考考你的记性，勾股定理的应用之，问题情境，牛刀小试，正方体中的最值问题，检测题四，台阶中的最值问题，AB25等内容，欢迎下载使用。

1、勾股定理的文字及符号语言2、在平面上如何求点与点、点与线的最短路径，依据什么？（1）两点之间线段最短（2）垂线段最短3、那么如何求某些几何体中的最短路径呢？
求解几何体的最短路线长
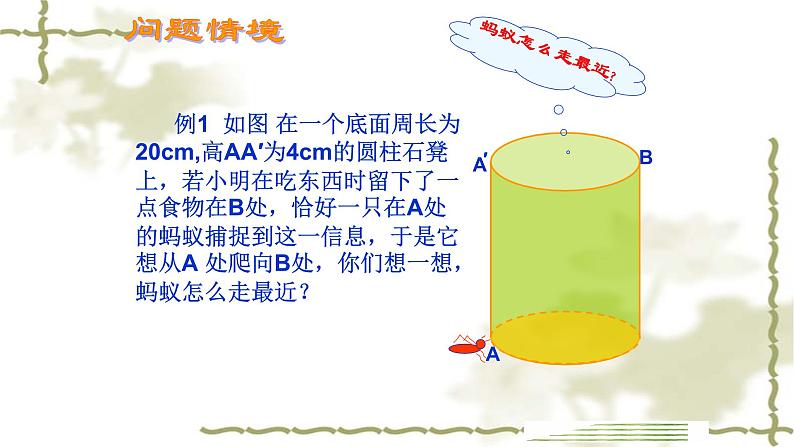
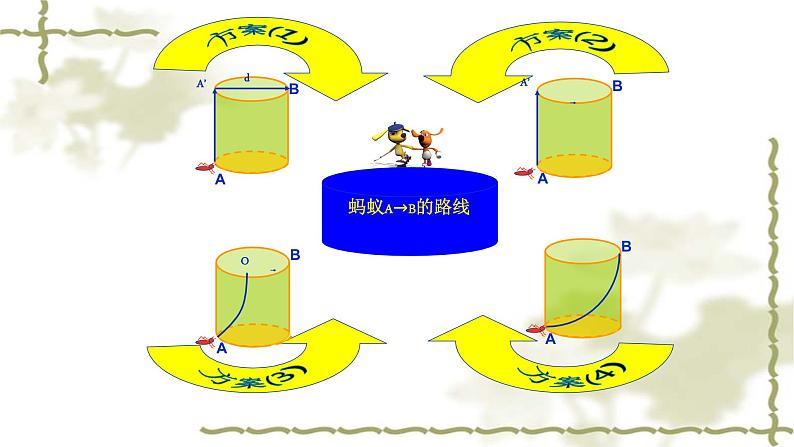
例1 如图 在一个底面周长为20cm,高AA′为4cm的圆柱石凳上，若小明在吃东西时留下了一点食物在B处，恰好一只在A处的蚂蚁捕捉到这一信息，于是它想从A 处爬向B处，你们想一想，蚂蚁怎么走最近？
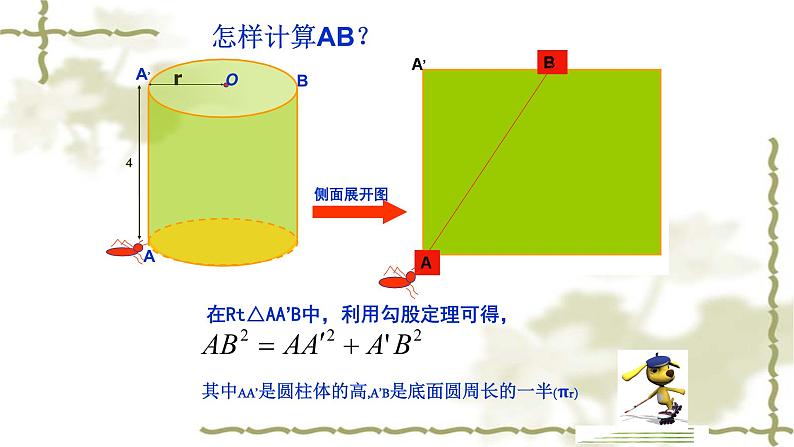
在Rt△AA’B中，利用勾股定理可得，
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
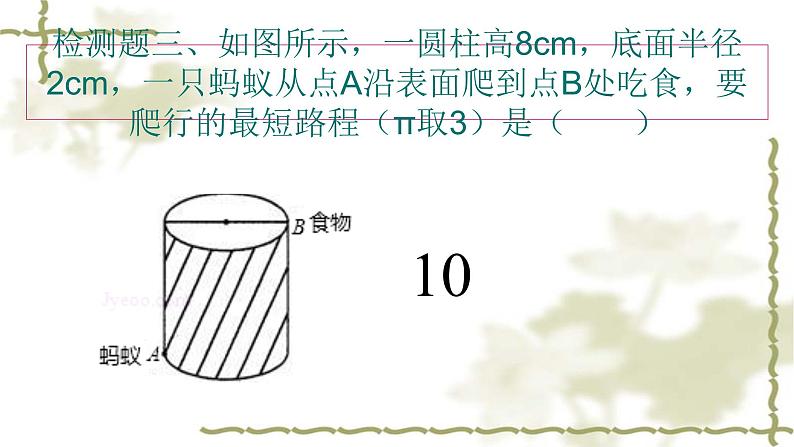
检测题三、如图所示，一圆柱高8cm，底面半径2cm，一只蚂蚁从点A沿表面爬到点B处吃食，要爬行的最短路程（π取3）是（　　）
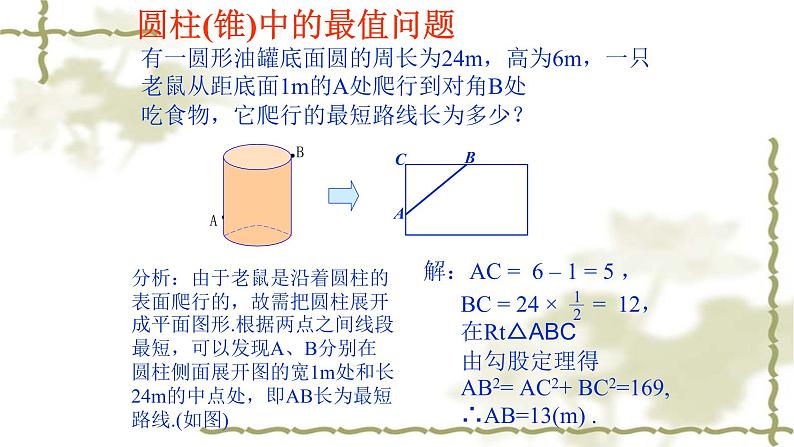
圆柱(锥)中的最值问题
有一圆形油罐底面圆的周长为24m，高为6m，一只老鼠从距底面1m的A处爬行到对角B处吃食物，它爬行的最短路线长为多少？
分析：由于老鼠是沿着圆柱的表面爬行的，故需把圆柱展开成平面图形.根据两点之间线段最短，可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处，即AB长为最短路线.(如图)
如图，有一圆柱形油罐，现要从油罐底部的一点A环绕油罐建梯子，并且要正好建到A点正上方的油罐顶部的B点，已知油罐高AB=5米，油罐底部周长为12米，那么梯子最短要多少米？
例2、如图，边长为1的正方体中，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是（ ）. （A）3 （B） √5 （C）2 （D）1
分析： 由于蚂蚁是沿正方体的外表面爬行的，故需把正方体展开成平面图形（如图）.
检测题一：如图，一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B，则它走过的路程最短为（　　）
检测题二、如图是一个棱长为4cm的正方体盒子，一只蚂蚁在D1C1的中点M处，它到BB1的中点N的最短路线是（　　）
如图是一块长，宽，高分别是6cm，4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（　　）
第一种情况：把我们所看到的前面和上面组成一个平面，
则这个长方形的长和宽分别是9和4，
第二种情况：把我们看到的左面与上面组成一个长方形，
则这个长方形的长和宽分别是7和6，
第三种情况：把我们所看到的前面和右面组成一个长方形，
则这个长方形的长和宽分别是10和3，
三种情况比较而言，第二种情况最短
例4、如图，长方体的长为15 cm，宽为 10 cm，高为20 cm，点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B，需要爬行的最短距离是多少？
长方体中的最值问题（续）
如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
例1、如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是多少？
小 结： 把几何体适当展开成平面图形，再利用“两点之间线段最短”，或点到直线“垂线段最短”等性质来解决问题。
二、正方体中的最值问题
三、长方体中的最值问题