人教版八年级上册11.1.1 三角形的边学案

展开

这是一份人教版八年级上册11.1.1 三角形的边学案，共4页。学案主要包含了自主学习，合作探究，交流展示，拓展延伸，课堂检测等内容，欢迎下载使用。

学习目标：
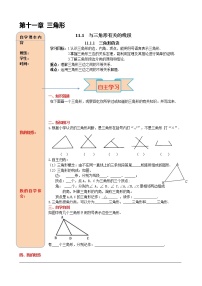
1、知识与技能: 了解三角形的意义,认识三角形的边、内角、顶点，能用符号语言表示三角形；理解三角形三边不等的关系，会判断三条线段能否构成一个三角形,并能运用它解决有关的问题.
2、过程与方法:在观察、操作、推理、归纳等探索过程中，发展合情推理能力，逐步养成数学推理的习惯.
3、情感、态度与价值观:体会数学与现实生活的联系，增强克服困难的勇气和信心.
学习重点:三角形的有关概念和符号表示，三角形三边间的不等关系.
学习难点：用三角形三边不等关系判定三条线段可否组成三角形.
学习过程：
一、自主学习：
认真阅读课本（P2至P3 “探究”前），完成检测练习一：
1. 的图形叫三角形。
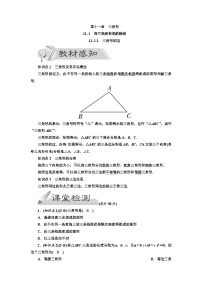
2.如图线段AB，BC，CA是三角形的，
点A，B，C是三角形的，∠ A、∠ B、 ∠ C是，叫做，简称。
3.用符号语言表示上图的三角形。
顶点是的三角形，记作，读作：。
4.按照三个内角的大小，可以将三角形分为
5.三角形按边可分为
二、合作探究，交流展示：
认真阅读课本（ P64“探究”）完成检测练习二：
1.在三角形ABC中，
AB+BC AC AC+BC AB AB+AC BC
2.假设一只小虫从点B出发，沿三角形的边爬到点C，
有路线。路线最近，根据是：，于是有：（得出的结论）。
3.下列长度的三条线段能否构成三角形，为什么？
(1)3、4、8 (2)5、6、11 (3)5、6、10
4.一个等腰三角形的周长为28cm.①已知腰长是底边长的3倍，求各边的长；
②已知其中一边的长为6cm,求其它两边的长.
解：
三、拓展延伸：
已知线段3cm,5cm,xcm,x为偶数，以3，5，x为边能组成______个三角形
四、课堂检测:
1.下列说法：
等边三角形是等腰三角形
三角形按边分类课分为等腰三角形、等边三角形、不等边三角形
三角形的两边之差大于第三边
三角形按角分类应分锐角三角形、直角三角形、钝角三角形
其中正确的是（）
A、1个 B、2个 C、3个 D、4个
2.一个不等边三角形有两边分别是3、5另一边可能是（）
A、1 B、2 C、3 D、4
3.下列长度的各边能组成三角形的是（）
A、3cm、12cm、8cm B、6cm、8cm、15cm C、3cm、5cm 、2 cm
D、6.3cm、6.3cm、12cm
4.已知等腰三角形的一边长等于4，另一边长等于9，求这个三角形的周长。
5.已知三角形的一边长为5cm,另一边长为3cm.则第三边的长取值范围是多少？
学（教）后反思：
答案
一、自主学习：
1.由三条线段首尾连接围成
2.边，顶点，相邻两边组成的角，三角形的内角，三角形的角。
3.A,B,C；△ABC；三角形ABC
4.锐角三角形、直角三角形、钝角三角形
不等边三角形
等腰三角形底和腰不相等的三角形
底和腰相等的三角形
二、合作探究，交流展示：
1.> > >
2.两；B-C；两点之间，线段最短；三角形两边的和大于第三边
3.(1)3、4、8 3+4<8,不能组成三角形
(2)5、6、11 5+6=11，不能组成三角形
(3)5、6、10 5+6>10，能组成三角形
4.解：①设底边长为xcm，则腰长是3xcm，
x+3x+3x=28，
解得：x=4,所以3x=12(cm)，
故，该等腰三角形的各边长为：4cm，12cm，12cm；
②若底边长为6cm，设腰长为ycm，
则：6+2y=28，
得：y=11，所以三边长分别为：6cm，11cm，11cm，
若腰长为6cm，设底边长为acm，
则：6+6+a=28，得a=16，又因为6+6=12<16，故舍去，
综上所述，该等腰三角形的三边长分别为：6cm，11cm，11cm.
三、拓展延伸：
2
四、课堂检测:
1. B 2.D 3.D
4.22
解：设第三边长为xcm，则5−3即2cm故答案为2cm

相关学案更多