2021年广西河池市凤山县初中学业水平模拟考试（二）数学试题（word版 含答案）

2021年广西河池市凤山县初中学业水平模拟考试（二）数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．下列各数中，比-2大的数是（    ）

A．-1 B．-2.5 C．-3 D．-3.5

2．如图，若，则的度数为（   ）

A． B． C． D．

3．下列调查中，适宜采用全面调查的是（     ）．

A．调查某池墙中现有鱼的数量

B．调查某批次汽车的抗撞击能力

C．选出某班短跑最快的学生参加全校短跑比赛

D．调查市场上某种食品的色素含量是否符合国家标准

4．下列几何体中的俯视图是三角形的是（    ）

A． B． C． D．

5．若6（y+2）=30,则y的值是(    )

A．6 B．3 C．2 D．1

6．因式分解（    ）

A． B． C． D．

7．下列计算中正确的是（   ）

A． B．

C． D．

8．一次函数的图象不经过（    ）．

A．第一象限 B．第二象限 C．第三象限 D．第四象限

9．已知点P（m﹣3，m﹣1）在第二象限，则m的取值范围在数轴上表示正确的是（　　）

A． B．

C． D．

10．如图，内接于，若，的半径，则阴影部分的面积为（    ）

A． B． C． D．

11．如图，在长为100 m，宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644m2，则道路的宽应为多少米？设道路的宽为x m，则可列方程为 (      )

A．100×80－100x－80x=7644 B．(100－x)(80－x)＋x2=7644

C．(100－x)(80－x)=7644 D．100x＋80x－x2=7644

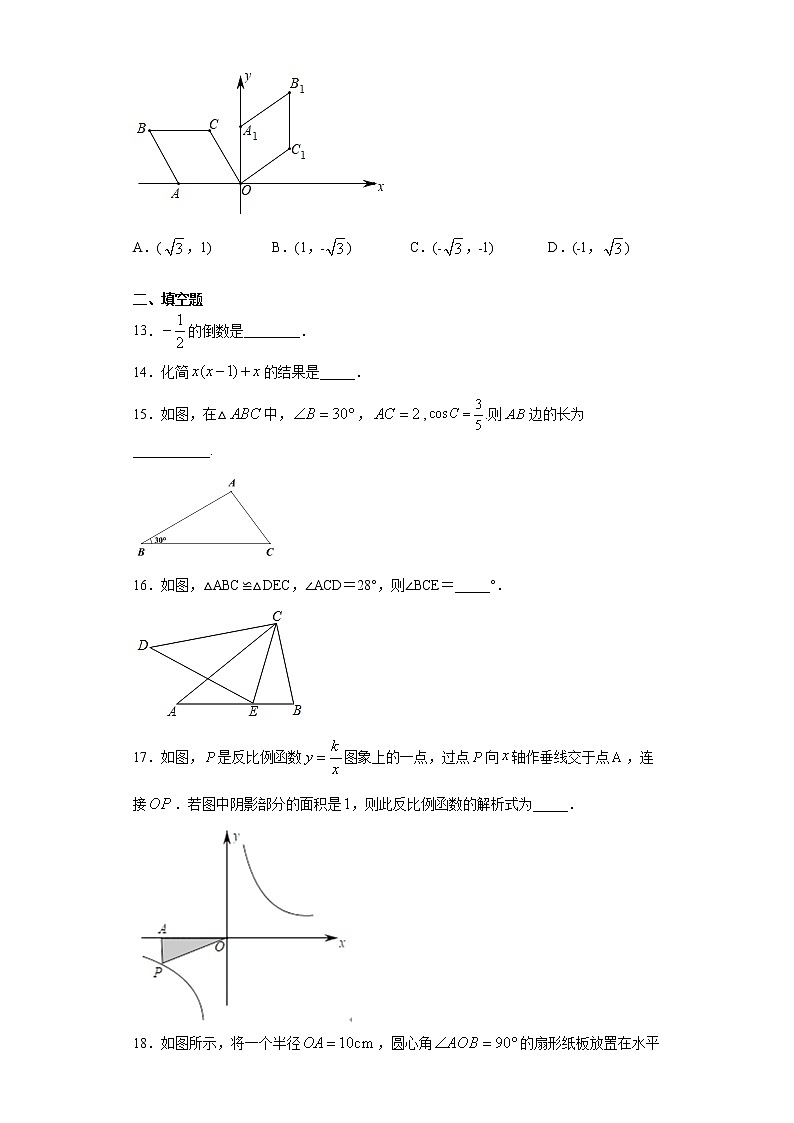
12．如图，菱形OABC的顶点O(0，0)，A(﹣2，0)，∠B＝60°，若菱形绕点O顺时针旋转90°后得到菱形OA1B1C1，依此方式，绕点O连续旋转2020次得到菱形OA2020B2020C2020，那么点C2020的坐标是（    ）

A．(，1) B．(1，﹣) C．(﹣，﹣1) D．(﹣1，)

二、填空题

13．的倒数是________．

14．化简的结果是_____．

15．如图，在△中，，,.则边的长为___________.

16．如图，△ABC≌△DEC，∠ACD＝28°，则∠BCE＝_____°．

17．如图，是反比例函数图象上的一点，过点向轴作垂线交于点，连接．若图中阴影部分的面积是，则此反比例函数的解析式为_____．

18．如图所示，将一个半径，圆心角的扇形纸板放置在水平面的一条射线上．在没有滑动的情况下，将扇形沿射线翻滚至再次回到上时，则半径的中点P运动的路线长为_____________．

三、解答题

19．计算：

20．解方程：．

21．如图，在平面直角坐标系中，已知的三个顶点坐标分别是，，．

（1）将向下平移5个单位长度后得到，请画出．

（2）将绕原点逆时针旋转90°后得到，请画出．

（3）判断以，，为顶点的三角形的形状．（无须说明理由）

22．甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等.比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）.依据统计数据绘制了如图所示的尚不完整的统计图表.

甲校成绩统计表

（1）在图①中，“7分”所在扇形的圆心角等于______；

（2）请你将②的统计图补充完整；

（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好；

（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？

23． 如图，在平行四边形ABCD中，E为BC边上一点，连结AE、BD且AE=AB

（1）求证：∠ABE=∠EAD；

（2）若∠AEB=2∠ADB，求证：四边形ABCD是菱形．

24．我市正在创建“全国文明城市”，某校拟举办“创文知识”抢答赛，欲购买A、B两种奖品以鼓励抢答者．如果购买A种20件，B种15件，共需380元；如果购买A种15件，B种10件，共需280元．

（1）A、B两种奖品每件各多少元？

（2）现要购买A、B两种奖品共100件，总费用不超过900元，那么A种奖品最多购买多少件？

25．如图，以AB为直径的经过的顶点C，过点O作交于点D，交AC于点F，连接BD交AC于点G，连接CD，在OD的延长线上取一点E，连接CE，使．

（1）求证：EC是的切线

（2）若的半径是3，，求CE的长．

26．抛物线与轴交于，两点，与轴交于点，已知点的坐标为，点的坐标为．

（1）求抛物线的解析式．

（2）如图甲，若为上方抛物线上的一个动点，当的面积最大时，求点的坐标．

（3）如图乙，为该抛物线的顶点，直线轴于点，在直线上是否存在点，使点到直线的距离等于点到点的距离？若存在，求出点的坐标；若不存在，请说明理由．

参考答案

1．A

【分析】

两个负数，绝对值大的其值反而小，据此判断即可．

【详解】

解：根据有理数比较大小的方法，可得
-3.5＜-2.5＜-2＜-1，
所以各数中，比-2大的数是-1．
故选：A．

【点睛】

此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确两个负数，绝对值大的其值反而小．

2．B

【分析】

根据两直线平行，同位角相等即可得出答案．

【详解】

，

，

故选：B．

【点睛】

本题主要考查平行线的性质，掌握平行线的性质是解题的关键．

3．C

【分析】

根据全面调查和抽样调查的特点逐一分析即可．

【详解】

解：A．调查某池塘中现有鱼的数量，应采用抽样调查，故此选项不合题意；

B．调查某批次汽车的抗撞击能力，应采用抽样调查，故此选项不合题意；

C．选出某班短跑最快的学生参加全校短跑比赛，适宜采用全面调查，故此选项符合题意；

D．调查市场上某种食品的色素含量是否符合国家标准，应采用抽样调查，故此选项不合题意．

故选：C．

【点睛】

本题考查了抽样调查和全面调查的区别，选择全面调查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

4．C

【分析】

根据从上面看得到的图象是俯视图，可得答案．

【详解】

解：A、圆柱的俯视图是圆，故此选项不合题意；

B、圆锥的俯视图是有圆心的圆，故此选项不合题意；

C、三棱柱的俯视图是三角形，故此选项符合题意；

D、四棱锥的俯视图是矩形，故此选项不合题意；

故选：C．

【点睛】

本题考查了简单组合体的三视图，从上面看的到的视图是俯视图．

5．B

【分析】

将方程化简计算即可.

【详解】

解：，两边除以6得：

所以，

故选：B．

【点睛】

本题主要考查一元一次方程的解法，熟悉解方程的步骤是解题的关键.

6．C

【分析】

根据完全平方公式进行因式分解即可．

【详解】

．

故选C．

【点睛】

本题考查运用公式法进行因式分解，解题关键在于对公式的熟练掌握与应用，题目比较简单．

7．C

【分析】

各项分别计算得到结果，即可作出判断.

【详解】

A. ,故本选项错误.

B．，本选项错误；

C. ,本选项正确；

D. ,本选项错误.

故选C.

【点睛】

本题考查学生的计算能力，解题的关键是熟练运用整式的运算法则，本题属于基础题型．

8．C

【分析】

根据一次函数图像、直角坐标系的性质分析，即可得到答案．

【详解】

当时，

当时，

∴一次函数的图象如下：

∴一次函数的图象不经过第三象限

故选：C．

【点睛】

本题考查了一次函数、直角坐标系的知识；解题的关键是熟练掌握一次函数的图像，从而完成求解．

9．D

【分析】

先根据题意列出不等式组，求出其中各不等式的解集，再求出这些解集的公共部分即可．

【详解】

解：∵点P（m﹣3，m﹣1）在第二象限，

∴，

解得：1＜m＜3，

故选D．

【点睛】

本题考查不等式组的解法，在数轴上表示不等式组的解集等知识，解题的关键是熟练掌握不等式组的解法，属于中考常考题型．

10．A

【分析】

根据圆周角定理，再结合扇形面积公式和三角形面积公式，即可得出答案.

【详解】

解：∵，

∴，

∴阴影部分的面积，

故选A．

【点睛】

本题考查圆周角定理、结合扇形面积公式、三角形面积公式，解题的关键是熟练掌握圆周角定理、结合扇形面积公式、三角形面积公式.

11．C

【详解】

试题分析：设道路的宽应为x米，由题意有

（100﹣x）（80﹣x）=7644，

故选C

考点: 由实际问题抽象出一元二次方程

12．D

【分析】

如图（见解析），作于D，先根据菱形的性质得出，再根据直角三角形的性质得出，从而可得点C的坐标为，然后菱形OABC绕点O连续旋转2020次，旋转4次为一周，绕点O连续旋转2020次得到菱形与菱形OABC重合，从而可得点与C重合，由此即可得出答案．

【详解】

如图，作于点D，则，

∵四边形OABC是菱形，，，

∴，

∴，

∴，

∴点C的坐标为，

若菱形绕点O顺时针旋转后得到菱形，依此方式，绕点O连续旋转2020次得到菱形，则菱形OABC绕点O连续旋转2020次，旋转4次为一周，旋转2020次为（周），

∴绕点O连续旋转2020次得到菱形与菱形OABC重合，

∴点与C重合，

∴点的坐标为，

故选：D．

【点睛】

本题考查了菱形的性质、直角三角形的性质、图形的旋转，根据图形的旋转方式，正确得出一般规律是解题关键．

13．－2

【详解】

的倒数是：，本题考查了倒数的概念，即当a≠0时,a与互为倒数．特别要注意的是：负数的倒数还是负数，此题难度较小．

14．

【分析】

直接去括号然后合并同类项即可．

【详解】

解：，

故答案为：．

【点睛】

本题考查了整式运算，涉及了单项式乘以多项式、合并同类项等知识点，熟练掌握运算性质是解题的关键．

15．

【分析】

过A作AD⊥BC于D点，根据，可求得CD，在Rt△ACD中由勾股定理可求得AD，再利用Rt△ADB中，可知AB=2AD，即可解题

【详解】

过A作AD⊥BC于D点，

∵，AC=2

∴CD=

在Rt△ACD中由勾股定理得：AD=

又∵∠B=30°

∴AB=2AD=.

【点睛】

本题考查了锐角三角函数，勾股定理求线段长度，30°所对的直角边是斜边的一半，灵活联合运用即可解题.

16．28

【分析】

根据全等三角形对应角相等可得∠ACB＝∠DCE，再根据等式的性质两边同时减去∠ACE可得结论．

【详解】

证明：∵△ABC≌△DEC，

∴∠ACB＝∠DCE，

∴∠ACB﹣∠ACE＝∠DCE﹣∠ACE，

即∠ACD＝∠BCE＝28°．

故答案是：28．

【点睛】

本题考查了全等三角形的性质，三角形的内角和定理的应用，能熟记全等三角形的性质是解此题的关键，注意：全等三角形的对应角相等．

17．．

【分析】

根据反比例函数系数的几何意义可知，的面积，再根据图象所在象限求出的值即可．

【详解】

解：依据比例系数的几何意义可得，

面积等于，

即，

，

由于函数图象位于第一、三象限，则，

反比例函数的解析式为；

故答案为．

【点睛】

本题考查反比例系数的几何意义，过双曲线上的任意一点分别向两条坐标作垂线，与坐标轴围成的矩形面积就等于．

18．无解

【详解】

中考错题无解

19．

【分析】

根据绝对值、零指数幂、三角函数、负指数幂、二次根式的运算法则计算即可．

【详解】

=

【点睛】

本题考查绝对值、零指数幂、三角函数、负指数幂、二次根式的混合运算,关键在于牢记运算法则．

20．

【分析】

等式两边同时乘以去分母，将分式方程化为整式方程，求解即可．

【详解】

解：去分母，得．

去括号，得．

解得．

经检验，是原方程的解．

原方程的解是．

【点睛】

本题考查解分式方程，掌握分式方程的求解方法是解题的关键，注意要验根．

21．（1）作图见解析；（2）作图见解析；（3）等腰直角三角形．

【分析】

（1）分别作出、、的对应点、、，然后再连接、、，即可；

（2）分别作出、、绕原点逆时针旋转90°后的对应点、、，然后再连接、、即可；

（3）以，，为顶点的三角形的是等腰直角三角形，利用勾股定理以及勾股定理的逆定理判断即可．

【详解】

解：（1）如图所示，即为所求；

（2）如图所示，即为所求；

（3）为等腰直角三角形；

理由：∵，,，

∴，OB=OA1，

所以为等腰直角三角形．

【点睛】

本题考查平移作图，旋转作图，勾股定理以及逆定理等知识，熟练掌握基本知识是解题的关键．

22．（1）144°；（2）乙校得8分的学生的人数为3人，据此可将图②的统计图补充完整如图③见解析；（3）从平均分和中位数的角度分析乙校成绩较好；（4）应选甲校.

【分析】

(1)观察图①、图②，根据10分的人数以及10分的圆心角的度数可以求出乙校参赛的人数，然后再用360度乘以“7分”学生所占的比例即可得；

(2)求出8分的学生数，据此即可补全统计图；

(3)先求出甲校9分的人数，然后利用加权平均数公式求出甲校的平均分，根据中位数概念求出甲校的中位数，结合乙校的平均分与中位数进行分析作出判断即可；

(4)根据两校的高分人数进行分析即可得.

【详解】

(1)由图①知“10分”的所在扇形的圆心角是90度，由图②知10分的有5人，所以乙校参加英语竞赛的人数为：5÷=20(人)，

所以“7分”所在扇形的圆心角=360°×=144°，

故答案为144；

(2)乙校得8分的学生的人数为(人)，

补全统计图如图所示：

(3)由(1)知甲校参加英语口语竞赛的学生人数也是20人，

故甲校得9分的学生有(人)，

所以甲校的平均分为：(分)，中位数为7分，

而乙校的平均数为8.3分，中位数为8分，

因为两校的平均数相同，但甲校的中位数要低于乙校，所以从平均分和中位数的角度分析乙校成绩较好；

(4)选8名学生参加市级口语团体赛，甲校得10分的有8人，而乙校得10分的只有5人，所以应选甲校.

【点睛】

本题考查了条形统计图和扇形统计图的综合运用，中位数等知识，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．

23．（1）证明见解析；（2）证明见解析．

【分析】

（1）根据平行四边形的对边互相平行可得AD∥BC，再根据两直线平行，内错角相等可得∠AEB=∠EAD，根据等边对等角可得∠ABE=∠AEB，即可得证．

（2）根据两直线平行，内错角相等可得∠ADB=∠DBE，然后求出∠ABD=∠ADB，再根据等角对等边求出AB=AD，然后利用邻边相等的平行四边形是菱形证明即可．

【详解】

证明：（1）∵在平行四边形ABCD中，AD∥BC，

∴∠AEB=∠EAD．

∵AE=AB，

∴∠ABE=∠AEB．

∴∠ABE=∠EAD．

（2）∵AD∥BC，

∴∠ADB=∠DBE．

∵∠ABE=∠AEB，∠AEB=2∠ADB，

∴∠ABE=2∠ADB．

∴∠ABD=∠ABE－∠DBE=2∠ADB－∠ADB=∠ADB．

∴AB=AD．

又∵四边形ABCD是平行四边形，

∴四边形ABCD是菱形．

24．（1）A种奖品每件16元，B种奖品每件4元．（2）A种奖品最多购买41件．

【详解】

【分析】（1）设A种奖品每件x元，B种奖品每件y元，根据“如果购买A种20件，B种15件，共需380元；如果购买A种15件，B种10件，共需280元”，即可得出关于x、y的二元一次方程组，解之即可得出结论；

（2）设A种奖品购买a件，则B种奖品购买（100﹣a）件，根据总价=单价×购买数量结合总费用不超过900元，即可得出关于a的一元一次不等式，解之取其中最大的整数即可得出结论．

【详解】（1）设A种奖品每件x元，B种奖品每件y元，

根据题意得：，

解得：，

答：A种奖品每件16元，B种奖品每件4元；

（2）设A种奖品购买a件，则B种奖品购买（100﹣a）件，

根据题意得：16a+4（100﹣a）≤900，

解得：a≤，

∵a为整数，

∴a≤41，

答：A种奖品最多购买41件．

【点睛】本题考查了一元一次不等式的应用以及二元一次方程组的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据不等关系，正确列出不等式.

25．（1）见解析；（2）

【分析】

（1）连接OC,由AB是直径及可得，进而得到，再根据圆周角定理推导出，进而得到，再根据OC是半径即可得证；

（2）由（1）得，进而得到，再通过证明得到，再由即可求出CE的值.

【详解】

（1）证明：如图，连接OC，

∵AB是直径，

∴，

∵，

∴，

∴，

∵，

∴，

∵，

∴，

∴，

∵，

∴，即，

∴，

又∵OC是半径，

∴是切线．

（2）由（1）得，

∴，

∵，

∴，

∴ ，

∴，

又∵，

∴，

∴，

∴ ，

∴，

∵，

∴是等边三角形，

∴ ，

在中，

∴，

∴.

【点睛】

本题考查切线的判定、圆周角定理、相似三角形的判定等知识，熟知切线的判定方法以及相似三角形的性质是解题的关键.

26．（1）；（2）；（3）存在；点的坐标为或．

【分析】

（1）用待定系数法求出抛物线解析式；

（2）过点作轴于点，交于点，设点的坐标为，先求出直线的解析式，再用m表示，得出，配方即可得出结论

（3）先根据抛物线的解析式得出顶点M的坐标, 设点坐标为，得出，从而确定NG的长，再根据得到关于n的方程，解方程即可

【详解】

（1）由题意得解得

抛物线的解析式为．

（2）设点的坐标为，如图，

过点作轴于点，交于点．

点的坐标为，点的坐标为，

直线的解析式为．

点的坐标为．

．

当时，取得最大值，此时点的坐标为．

（3）存在点满足要求．

，

顶点的坐标为．

直线的解析式为．

设直线与轴交于点，

则点的坐标为．

．

．

设满足要求的点坐标为，

则．

如图，过点作于点，

则．

，

．

又，

．

整理得．

解得．

存在点满足要求，点的坐标为或．

【点睛】

本题是二次函数的综合题，解题的关键是熟练掌握待定系数法可求抛物线的解析式，三角形面积公式，二次函数的最值，抛物线的顶点坐标，两点间的距离公式，以及方程思想的应用，综合性较强．