

广东省中山市2020-2021学年八年级数学下学期期末预测卷(word版 含答案)
展开2021年广东省中山市八年级数学下册期末预测卷
一、单项选择题(共10个小题,每小题3分,满分30分)
1.已知x>2,则下列二次根式定有意义的是( )
A. 2-x B. x-1 C. x-3 D. x-4
2.小明同学一周的体温监测结果如表:
星期
一
二
三
四
五
六
日
体温(单位:°C)
36.7
36.0
36.6
36.3
36.2
36.6
36.4
分析表中的数据,众数、中位数、平均数分别是( )
A. 36.6,36.4,36.4 B. 36.0,36.4,36.7 C. 36.0,36.3,36.4 D. 36.6,36.3,36.7
3.如图,小明将一张长为 20cm ,宽为 15cm 的长方形纸 (AE>DE) 剪去了一角,量得 AB=3cm , CD=4cm ,则 BC 长为( )
A. 20cm B. 16cm C. 12cm D. 5cm
4.下列计算正确的是( )
A. 2 + 3 = 5 B. 2 - 3 =1 C. 2 ÷ 3 = 63 D. 2 × 3 =6
5.数据2021, 2021, 2021, 2021 , 2021, 2021, 2021, 2021的方差是( )
A. 2021 B. 0 C. -2021 D. 2020
6.已知▱ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A. DE=BE B. ∠DEA= 12 ∠DAB C. ∠DEA=∠BAE D. AD=DE
7.如图,矩形纸片ABCD中,点E是AD的中点,且AE=2,BE的垂直平分线MN恰好过点C,则矩形的一边AB的长度为( )
A. 2 B. 2 5 C. 4 D. 2 3
8.如果函数 y=kx-2021 中的 y 随 x 的增大而减小,那么这个函数的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
9.已知点A(a,m)和点B(﹣a﹣2,n)都在正比例函数y=﹣3x的图象上,则m+n的值为( )
A. 3 B. ﹣3 C. ﹣6 D. 6
10.如图,如图正方形 ABCD 内一点E , 满足 △CDE 为正三角形,直线AE交BC于F点,过E点的直线 GH⊥AF ,交AB于点G , 交CD于点H . 以下结论:① ∠AFC=105° ;② GH=2EF ;③ 2CE=EF+EH ;④ AEEH=23 ,其中正确的有( )
A. ①②③ B. ①③④ C. ①④ D. ①②③④
二、填空题(共7个小题,每小题4分,满分28分)
11.某校,为从甲、乙两名初三学生中选出一人参加长沙市一中2020年生物夏令营海滨野外实习活动,特统计了他们最近10次生物考试成绩.其中,他们的平均成绩都为95分,方差分别是 S甲2 =0.8, S乙2 =1.3,从稳定性的角度来看,________的成绩更稳定.(填“甲”或“乙”)
12.若 y=x-4+4-x2-2 则 (x+y)y ________.
13.如图,在△ABC中,AB=AC,延长CB至点E,点D在AC边上,以CE,CD为边作Y ▱ DCEF.若∠F=70°,则∠A的度数为________度.
14.在边长为2的正方形 ABCD 中,点E是 AB 的中点, EF⊥BD 于点F , 则 EF 的长度________.
15.已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:
x
- 2
- 1
0
1
2
3
y
6
4
2
0
- 2
- 4
那么方程ax+b =0的解是________;不等式ax+b>0的解集是________.
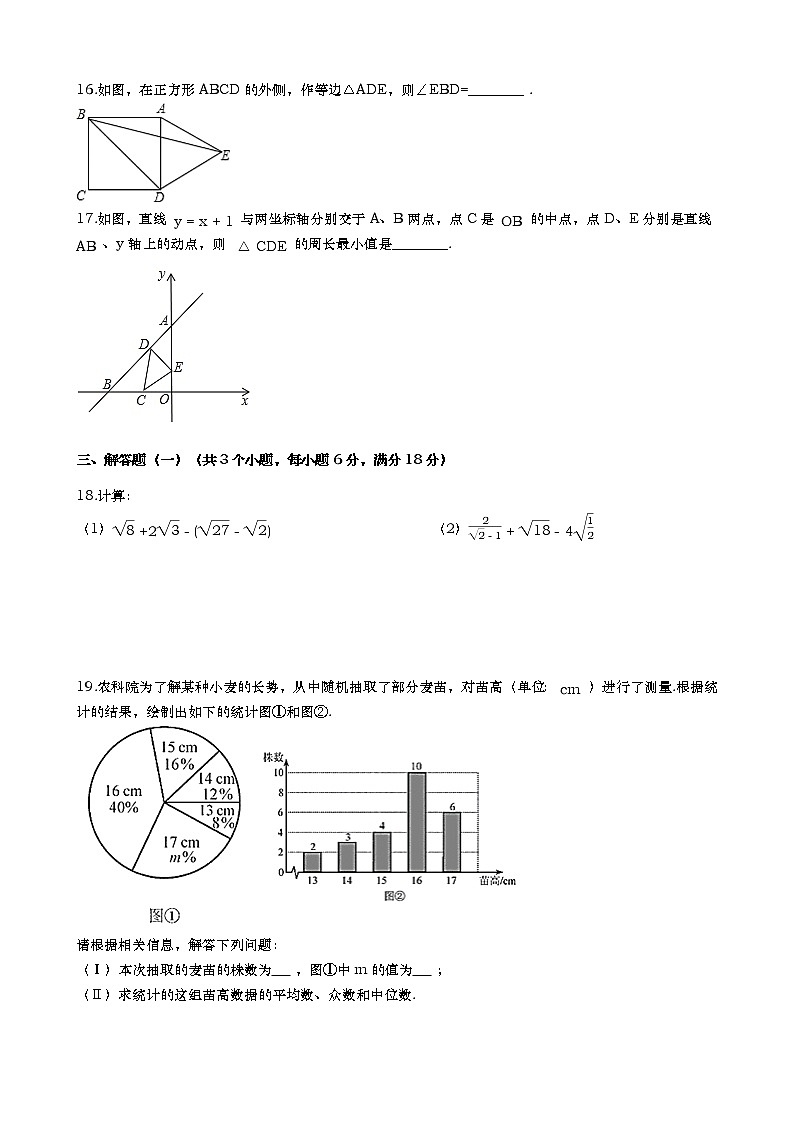
16.如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=________ .
17.如图,直线 y=x+1 与两坐标轴分别交于A、B两点,点C是 OB 的中点,点D、E分别是直线 AB 、y轴上的动点,则 △CDE 的周长最小值是________.
三、解答题(一)(共3个小题,每小题6分,满分18分)
18.计算:
(1)8+23-(27-2) (2)22-1+18-412
19.农科院为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: cm )进行了测量.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次抽取的麦苗的株数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组苗高数据的平均数、众数和中位数.
20.如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,6秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果精确到0.1米, 2 =1.414, 3 =1.732)
四、解答题(二)(共3个小题,每小题8分,满分24分)
21.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离)(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:
(1)A,B两城相距________千米;
(2)分别求甲、乙两车离开A城的距离y与x的关系式。
(3)求乙车出发后几小时追上甲车?
22.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为________,CD的长为________,AD的长为________.
23.如图,四边形 ABCD 为矩形,G是对角线 BD 的中点.连接 GC 并延长至F,使 CF=GC ,以 DC 、 CF 为邻边作 ▱DCFE ,连接 CE .
(1)若四边形 DCFE 是菱形,判断四边形 CEDG 的形状,并证明你的结论.
(2)在(1)条件下,连接 DF ,若 BC=3 ,求 DF 的长.
五、解答题(三)(共2个小题,每小题10分,满分20分)
24.如图, RtΔABC 中, ∠C=90° , D 是 AB 上一点, DE⊥AC 于点 E , F 是 AD 的中点, FG⊥BC 于点 G ,与 DE 交于点 H ,若 FG=AF , AG 平分 ∠CAB ,连结 GE , GD .
(1)求证: ΔECG≌ΔGHD ;
(2)求证: AD=AC+EC .
(3)若 ∠B=30° ,判定四边形 AEGF 是否为菱形,并说明理由.
25.如图,直角坐标系 xOy 中,过点 A(6,0) 的直线 l1 与直线 l2 : y=kx-1 相交于点 C(4,2) ,直线 l2 与x轴交于点B.
(1)k的值为________;
(2)求 l1 的函数表达式和 S△ABC 的值;
(3)直线 y=a 与直线 l1 和直线 l2 分别交于点M,N,(M,N不同)
①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以 MN 为边作正方形 MNDE ,边 DE 恰好在x轴上,直接写出此时a的值.
答案
一、选择题
1.解:∵x>2,
∴x﹣2>0,
∴2﹣x<0,x﹣1>0,x﹣3与x﹣4不一定大于0,
则当x>2时, x-1 有意义.
故答案为:B.
2.解:这组数据中36.6出现了2次,次数最多,所以众数是36.6;
将数据按照从小到大(或从大到小)的顺序排列为36.0,36.2,36.3,36.4,36.6,36.6,36.7
处于中间的数据是36.4,所以中位数是36.4;
平均数是=17×(36.0+36.2+36.3+36.4+36.6+36.6+36.7)=36.4.
故答案选:A.
3.延长AB,DC交于点F,
∵四边形AFDE是矩形,
∴ AF⊥DF ,
∴∠AFC=90° .
∵BF=AF-AB=15-3=12cm,FC=FD-CD=20-4=16cm ,
∴BC=BF2+FC2=122+162=20cm .
故答案为:A.
4.解:A.2和3不是同类二次根式,不能合并,故选项A错误;
B.2和3不是同类二次根式,不能合并,故选项B错误;
C.2÷3=23=63 , 故选项C正确;
D.2×3=6 , 故选项D错误.
故答案为:C.
5.解:∵这组数据全部相等,均为2021,
∴这组数据没有波动,
∴这组数据的方差为0,
故答案为:B.
6.解:由作法得AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠DEA=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE,∠DEA= 12 ∠DAB,
当AD=AB时可得到ED=EB,此时四边形ABCD为菱形,
∴DE=BE不一定成立.
故答案为:A.
7.解:连接EC,
∵矩形ABCD,点E是AD的中点,AE=2
∴AD=BC=2AE=4,DE=AE=2,∠D=90°,
∵BE的垂直平分线MN恰好过点C,
∴CE=BC=4,
在Rt△CDE中,
AB=CD=CE2-DE2=42-22=23.
故答案为:D.
8.解:∵一次函数 y=kx-2021 ,y随x的增大而减小,
∴k<0,
∵b=-2021<0,
∴此函数的图象经过二、三、四象限,不经过第一象限.
故答案为:A.
9.∵点A(a,m)和点B(﹣a﹣2,n)都在正比例函数y=﹣3x的图象上,
∴m=-3a,n=3a+6,
∴m+n=-3a+3a+6=6,
故答案为:D.
10.解: ∵ΔCDE 为正三角形,
∴∠CDE=60° ,
∴∠ADE=90°-60°=30° ,
∵AD=DE=CD ,
∴∠DAE=∠DEA=12(180°-30°)=75° ,
∴∠BAF=90°-75°=15° ,
∴∠AFC=90°+15°=105° ,故①符合题意;
过点H作 HK⊥AB ,
则 HK=AD ,
∵GH⊥AF ,
∴∠BAF+∠AGE=90° ,
又 ∵∠AGE+∠KHG=90° ,
∴∠BAF=∠KHG ,
在 ΔABF 和 ΔHKG 中,
{∠BAF=∠KHG∠B=∠HKG=90°HK=AB ,
∴ΔABF≅ΔHKG(AAS) ,
∴AF=GH ,
∵ΔCDE 为正三角形,
∴ 点E在 CD 的垂直平分线上,
根据平行线分线段成比例定理,点E是 AF 的中点,
∴AF=2EF ,
∴GH=2EF ,故②符合题意;
∵GH⊥AF , ∠DEA=75° ,
∴∠DEH=90°-75°=15° ,
∴∠CEH=60°-15°=45° ,
∴∠CEF=90°-45°=45° ,
过点F作 FM⊥CE 于M,过点H作 HN⊥CE 于N,
则 MF=EM , NH=EN ,
∵ΔCDE 是等边三角形,
∴∠DCE=60° ,
∴∠ECF=90°-60°=30° ,
∴CM=3MF , NH=3CN ,
∴CE=3MF+MF=3CN+CN ,
∴MF=CN ,
∴CE=22EF+22EH ,
∴ 2CE=EF+EH ,故③符合题意;
AEEH=EFEH=2MF3CN⋅2=33 ,故④不符合题意.
综上所述,正确的结论是①②③.
故答案为:A.
二、填空题
11.解:∵ S甲2 =0.8, S乙2 =1.3,
∴ S甲2
故答案为:甲.
12.解:∵x-4和4-x有意义,
∴x-4≥04-x≥0 ,
∴x=4,
∴y=-2,
∴(x+y)y=(4-2)-2=14.
13.解:∵ ▱ DCEF ,
∴∠C=∠F=70°,
∵AB=AC,
∴∠A=180°-2∠C=180°-140°=40°,
故答案为:40.
14.解:∵四边形 ABCD 是正方形,
∴ ∠ABD=45° ,
∵ AB=2 ,点E是 AB 的中点,
∴ BE=12AB=1 ,
∵ EF⊥BD , ∠ABD=45° ,
∴ ∠EFB=90° ,EF=BF ,
∴ BE=EF2+BE2=EF2+EF2=2EF ,
∴ EF=22BE=22
故答案为: 22 .
15.由表格可以看出,y=0时,即ax+b=0时,x=1;y>0,即ax+b>0时,x<1.
16.解:因为四边形ABCD是正方形,
所以AB=AD,∠BAD=90°,∠ABD=45°.
因为△ADE是等边三角形,
所以AD=AE,∠DAE=60°,
所以AB=AE,∠BAE=150°,
所以∠EBA= 12 (180°-150°)=15°,
所以∠EBD=∠ABD-∠EBA=45°-15°=30°.
故答案为30°.
17.解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,此时三角形CDE的周长最小,
∵直线y=x+1与两坐标轴分别交于A、B两点,
∴A(0,1),B(-1,0),
∴OA=OB,
∴∠ABC=45°,
∴△BCF是等腰直角三角形,
∵点C是OB的中点,
∴C( 12 ,0),
∴OG= 12 ,BG= 32 ,
∴ BF=BC=12 ,
由轴对称的性质,可得DF=DC,EC=EG,
△CDE的周长=CD+DE+CE=DF+DE+EG=FG,此时△DEC周长最小,
∵在Rt△BFG中,FG= BF2+BG2=(12)2+(32)2=102 ,
故答案为: 102 .
三、解答题
18. (1)解:原式= 22+23-33+2
=32-3
(2)解:原式= 2(2+1)(2-1)(2+1)+32-4×22
=22+2+32-22
=2+32
19. 解:(Ⅰ)由图②可知:
本次抽取的麦苗株数为:2+3+4+10+6=25(株),
其中17cm的麦苗株数为6株,故其所占的比为6÷25=0.24=24%,即m=24.
故答案为:25,24;(Ⅱ)观察条形统计图,
这组麦苗得平均数为: x=13×2+14×3+15×4+16×10+17×62+3+4+10+6=15.6 ,
∵ 在这组数据中,16出现了10次,出现的次数最多,
∴ 这组数据的众数为16.
∵ 将这组数据按从小到大的顺序排列,其中处于中间位置的数是16,
∴ 这组数据的中位数为16.
故答案为:麦苗高的平均数是15.6,众数是16,中位数是16.
20. 解:在Rt△ABC中,∠ABC=90°,BC=13m,AC=5m
∴AB= 132-52 =12
∵此人以0.5m/s的速度收绳,6s后移动到点D的位置
∴CD=13-0.5×6=10m
∴AD= CD2-AC2 = 102-52 = 53 m
∴BD=AB-AD=12- 53 ≈3.3m
答:船向岸边移到了大约3.3m
21.(1)300
(2)解:设甲对应的函数解析式为: y=kx,300=5k,
解得, k=60,
即甲对应的函数解析式为: y=60x ,
设乙对应的函数解析式为 y=mx+n ,
{m+n=04m+n=300 .
解得 m=100,n=-100.
即乙对应的函数解析式为 y=100x-100
(3)解:解方程组 {y=60xy=100x-100 ,
得: {x=2.5y=150 ,
2.5-1=1.5 ,即乙车出发后1.5小时追上甲车.
(1)由图像可知 A,B两城相距300千米,
故答案为:300.
22. (1)解:如图所示,AD为所求作的线段.
(2)25;5;5
23. (1)解:四边形 CEDG 是菱形,理由如下:
∵四边形 ABCD 为矩形,G是对角线 BD 的中点,
∴ GB=GC=GD ,
∵ CF=GC ,
∴ GB=GC=GD=CF ,
∵四边形 DCFE 是菱形,
∴ CD=CF=DE , DE//CG ,
∴ DE=GC ,
∴四边形 CEDG 是平行四边形,
∵ GD=GC ,
∴四边形 CEDG 是菱形
(2)解:∵ CD=CF , GB=GD=GC=CF ,
∴ △CDG 是等边三角形,
∴ CD=BG , GCD=∠DGC=60° ,
∴ ∠DCF=∠BGC=120° ,
∴ △BGC≌△DCF(SAS) ,
∴ DF=BC=3 .
24. (1)证明:∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∴∠CGE=∠GDE,
∴△ECG≌△GHD;
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)解:四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE= 12 AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
25. (1)k=34
(2)解:设直线 l1 的表达式为 y=k1x+b
将点 A(6,0) , C(4,2) 代入 {6k1+b=04k1+b=2 ,解得 {b=6k1=-1
直线 l1 的表达式为 y=-x+6 ,
当y=0时, 0=34x-1 ,解得 x=43 ,点B的坐标为 (43,0)
∴ SΔABC=12×(6-43)×2=143 ;
(3)① -1
解得:k= 34 ;
(3)
①当x=0时,y= 34 x﹣1=﹣1,y=﹣x+6=6,
∴M , N(M,N不同)都在y轴右侧时a的取值范围为﹣1<a<6且 a≠2 .
②当y=a时, 34 x﹣1=a ,
解得:x= 43 a+ 43 ,
∴点N的坐标为( 43 a+ 43 ,a);
当y=a时,﹣x+6=a ,
解得:x=6﹣a ,
∴点M的坐标为(6﹣a , a),
∴MN=|6﹣a﹣ 43 a﹣ 43 |=| 143 ﹣ 73 a|.
∵四边形MNDE为正方形,
∴| 143 ﹣ 73 a|=|a|,
解得:a1= 75 ,a2= 72 ,
∴a的值为 75 或 72 .
2020-2021学年广东省中山市八年级(上)期末数学试卷: 这是一份2020-2021学年广东省中山市八年级(上)期末数学试卷,共19页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
广东省中山市2020-2021学年九年级数学上期末模拟试卷(PDF版,含答案): 这是一份广东省中山市2020-2021学年九年级数学上期末模拟试卷(PDF版,含答案),共22页。
2021年广东省中山市香山区八年级(下)期末数学复习试卷 word版,含答案: 这是一份2021年广东省中山市香山区八年级(下)期末数学复习试卷 word版,含答案,共13页。试卷主要包含了下列运算正确的是,点P,如图为正比例函数y=kx等内容,欢迎下载使用。












