数学七年级上册1.4.1 有理数的乘法说课课件ppt

这是一份数学七年级上册1.4.1 有理数的乘法说课课件ppt，共20页。PPT课件主要包含了学习目标，多个有理数相乘，新课引入，一个负因数，积是负数，两个负因数，积是正数，三个负因数，四个负因数，例1计算等内容，欢迎下载使用。
1.理解并掌握多个有理数相乘时积的符号的确定;2.掌握有理数乘法交换律、结合律及乘法分配律；3.能够利用有理数的乘法运算律进行简便计算.
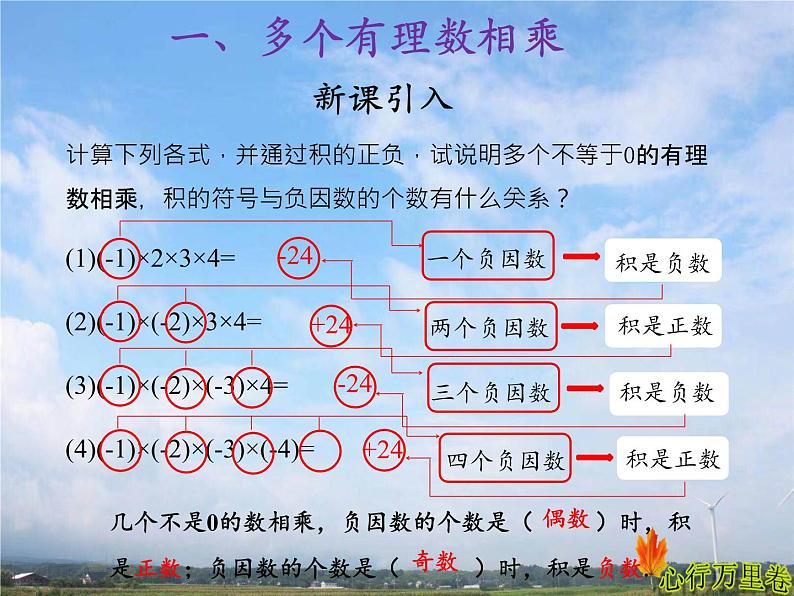
计算下列各式，并通过积的正负，试说明多个不等于0的有理数相乘，积的符号与负因数的个数有什么关系？(1)(-1)×2×3×4=(2)(-1)×(-2)×3×4=(3)(-1)×(-2)×(-3)×4=(4)(-1)×(-2)×(-3)×(-4)=
几个不是0的数相乘，负因数的个数是（ ）时，积是正数；负因数的个数是（ ）时，积是负数.
下式的结果是多少？为什么？(-1)×(-2)×(-3)×(-4)×0=
因为：几个数相乘，只要其中有一个因数为0，积就等于( ).
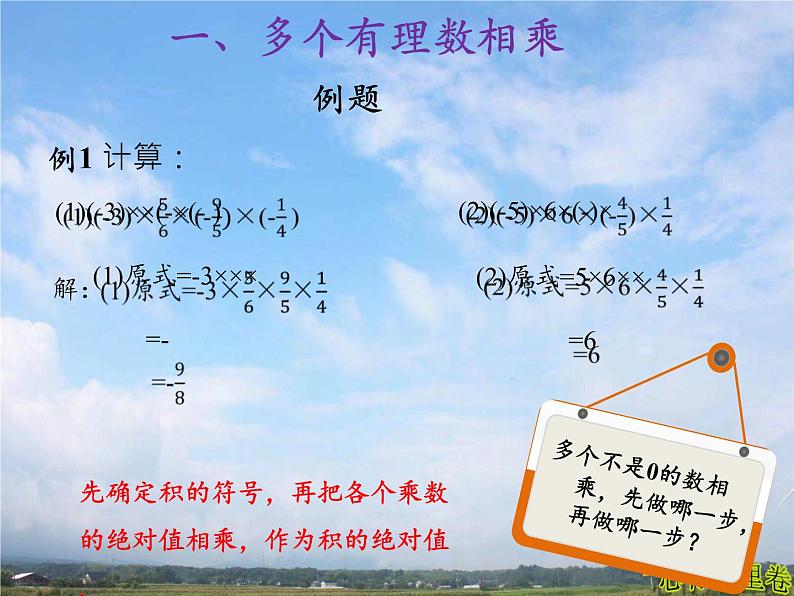
(1)(-3)××(-×(- )
(2)(-5)×6×(-)×
(1)原式=-3××× =-
(2)原式=5×6×× =6
先确定积的符号，再把各个乘数的绝对值相乘，作为积的绝对值.
积的符号确定几个不等于0的因数相乘，积的符号由负因数的个数决定.当负因数有奇数个时，积的符号为负；当负因数有偶数个时，积的符号为正.只要有一个因数为0，积就为0.
多个有理数相乘的解题步骤第一步：是否有因数0；第二步：确定符号（奇负偶正）；第三步：绝对值相乘.
1.几个不等于0的有理数相乘，积的符号由( )A.正因数的个数决定 B.负因数的个数决定C.因数的个数决定 D.负数的大小决定
2.若三个有理数的积为0，则(　　 )A.三个数都为0 B.两个数为0C.一个为0，另两个不为0 D.至少有一个为0
小学学过的乘法运算律有：乘法交换律、乘法结合律、乘法分配律.
用式子表示运算律为：乘法交换律：ab=ba乘法结合律：(ab)c=a(bc)乘法分配律：a(b+c)=ab+ac
思考：在有理数乘法中，上述运算律还成立吗？
(-7)×88×(-7)
(-7)×8=8×(-7)
两个数相乘，交换因数的位置，积相等.
[(-2)×(-6)]×5(-2)×[(-6)×5]
[(-2)×(-6)]×5=(-2)×[(-6)×5]
三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等.
(ab)c=a(bc)
4×[(-3)+5]4×(-3)+4×5
4×[(-3)+5]=4×(-3)+4×5
一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加.
a(b+c)=ab+ac
下列各式中用了哪条运算律？如何用字母表示？1.(-4)×8=8 ×(-4)2.[(-8)+5]+(-4)=(-8)+[5+(-4)]3.(-6)×[ +(- )]=(-6)× +(-6)×(- )4.[29×(- )] ×(-12)=29 ×[(- )×(-12)]
乘法交换律：ab=ba
分配律：a(b+c)=ab+bc
乘法结合律：(ab)c=a(bc)
加法结合律：（a+b)+c=a+(b+c)
例2 用两种方法计算：( - - )×16.
原式=( - - )×16 =- ×16 =-6
原式= ×16- ×16- ×16 =4-8-2 =-6
解法1先算括号里面的，再算括号外面的；解法2直接用括号里面的数分别和括号外面的数相乘,再进行计算.相比较来说，解法2的运算量小一些.
1.下列各式变形各用了哪些运算律？(1)1.25×(-4)×(-25)×8=(1.25×8)×[(-4)×(-25)](2)(+ - )×(-8)=( )×(-8)+( - )×(-8)(3)25×[+(-5)+ ]×(-)= 25×(- )×[(-5)+ + ]
（乘法交换律和结合律）
（加法结合律和乘法分配律）
（乘法交换律和加法结合律）
2.为使运算简便，如何把下列算式变形？(1)(- )×1.25×(-8)(2)(-10)×(-8.24) ×(-0.1)(3)(-)×2.4×
(1)(-85)×(-25)×(-4)；
3.用简便方法计算：
解：原式= (-85)×[(-25) ×(-4 )] =(-85)×100 =-8500
(2) ( - ) ×30；
解：原式= ×30- ×30 =27-2 =25
(3) (-)×(-)+(- )×
解：原式=-×(-+ ) =-×5 =-6
(4) -×15×(-1)
解：原式=-×15×(-) =-×(-)×15 =15