初中数学人教版九年级上册24.1.1 圆复习练习题

这是一份初中数学人教版九年级上册24.1.1 圆复习练习题，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(每小题的4个选项中只有一个符合题意，请将符合题目要求答案的英文字母代号填写在括号内，每题3分，共36分)
1．给定下列条件可以确定一个圆的是（ ）
A．已知圆心 B．已知半径
C．已知直径 D．不在同一直线上三点
2．如图，在⊙O中，弦AB为8cm，圆心O到AB的距离为3cm，则⊙O的半径等于（ ）
A．3cmB．4cmC．5cmD．8cm

2题图 4题图 6题图
3．下列命题：①同圆中等弧对等弦；②垂直于弦的直径平分这条弦；③平分弦的直径垂直于这条弦；④相等的圆心角所的弧相等．其中是真命题的是（ ）
A．①②B．①②③C．①③④D．②③④
4．如图，⊙O是△ABC的外接圆，∠BCO=20°，则∠A的度数为( )
A．60°B．65°C．70°D．75°
5．在Rt△ABC中，∠ACB=90°，AC=6，AB=10，以C为圆心，BC为半径作⊙C，则点A与⊙C的位置关系是（ ）
A．点A在⊙C内B．点A在⊙C上
C．点A在⊙C外D．无法确定
6．如图，△ABC内接于圆，∠ACB=90°，过点C的切线交AB的延长线于点P，∠P=28°．则∠CAB=（ ）
A．62°B．31°C．28°D．56°
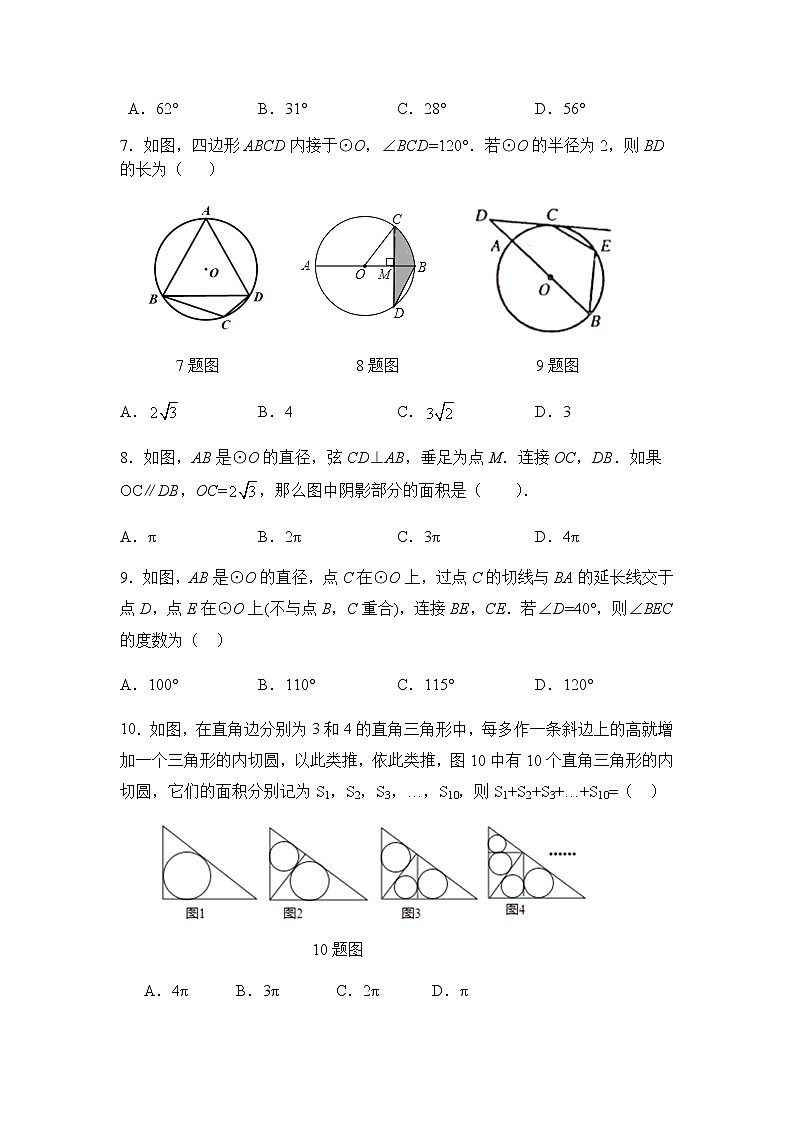
7．如图，四边形ABCD内接于⊙O，∠BCD=120°．若⊙O的半径为2，则BD的长为（ ）

7题图 8题图 9题图
A．B．4C．D．3
8．如图，AB是⊙O的直径，弦CD⊥AB，垂足为点M．连接OC，DB．如果OC∥DB，OC=，那么图中阴影部分的面积是（ ）．
A．πB．2πC．3πD．4π
9．如图，AB是⊙O的直径，点C在⊙O上，过点C的切线与BA的延长线交于点D，点E在⊙O上(不与点B，C重合)，连接BE，CE．若∠D=40°，则∠BEC的度数为（ ）
A．100°B．110°C．115°D．120°
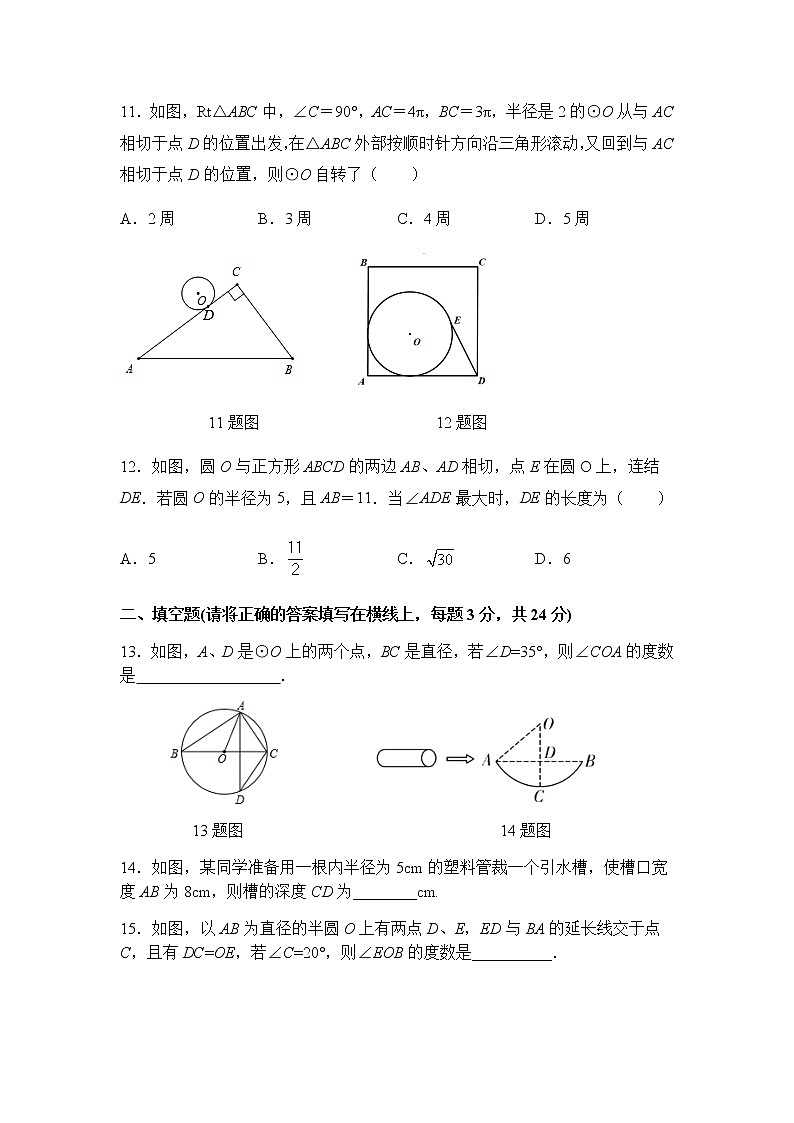
10．如图，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，以此类推，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10=（ ）

10题图
A．4π B．3π C．2π D．π
11．如图，Rt△ABC中，∠C＝90°，AC＝4π，BC＝3π，半径是2的⊙O从与AC相切于点D的位置出发，在△ABC外部按顺时针方向沿三角形滚动，又回到与AC相切于点D的位置，则⊙O自转了（ ）
A．2周B．3周C．4周D．5周

11题图 12题图
12．如图，圆O与正方形ABCD的两边AB、AD相切，点E在圆O上，连结DE．若圆O的半径为5，且AB＝11．当∠ADE最大时，DE的长度为（ ）
A．5B．C．D．6
二、填空题(请将正确的答案填写在横线上，每题3分，共24分)
13．如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠COA的度数是 ．

13题图 14题图
14．如图，某同学准备用一根内半径为5cm的塑料管裁一个引水槽，使槽口宽度AB为8cm，则槽的深度CD为________cm.
15．如图，以AB为直径的半圆O上有两点D、E，ED与BA的延长线交于点C，且有DC=OE，若∠C=20°，则∠EOB的度数是__________．

15题图 16题图
16．如图，A．B．C．D四点在⊙O上，OC⊥AB，∠AOC=40°，则∠BDC的度数是 .
17．如图，⊙O中，AC为直径，MA，MB分别切⊙O于点A，B．过点B作BD⊥AC于点E，交⊙O于点D，若BD=MA，则∠AMB的大小为 （度）．

17题图 18题图 20题图
18．如图，⊙O的半径为4，直线AB与⊙O相切于点A，AC平分∠OAB，交⊙O于点C．则的长为 ．
19．平面直角坐标系内，A(-1,0)，B(1,0)，C(4，﹣3)，P 在以 C 为圆心 1 为 半径的圆上运动，连接 PA，PB，则PA2+PB2的最小值是 .
20．将正方形ABCD绕点A按逆时针方向旋转30°，得正方形AB1C1D1，B1C1交CD于点E，AB＝，则四边形AB1ED的内切圆半径为 .
三、解答题(本题共8个小题，共60分)
21．(本题6分)已知：如图，四边形ABCD的顶点都在⊙O上，BD平分∠ADC，且BC=CD．求证： AB=CD．
21题图
22．(本题6分)在⊙O中，AB是非直径弦，弦CD⊥AB，
（1）当CD经过圆心时(如图①)，∠AOC+∠DOB= __________；
（2）当CD不经过圆心时(如图②)，∠AOC+∠DOB的度数与（1）的情况相同吗?试说明你的理由．
22题图
23．(本题6分)尺规作图：已知△ABC，如图．
（1）求作：△ABC的外接圆⊙O；
（2）若AC＝4，∠B＝30°，求△ABC的外接圆⊙O的半径．
23题图
24．(本题7分)如图，在△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．
（1）试判断直线BC与⊙O的位置关系，并说明理由；
（2）若BD＝2，BF＝2，求阴影部分的面积（结果保留π）．
24题图
25．(本题7分)如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为弧BE的中点，连接AD交BC于F，AC=FC，连接BD.
（1）求证：AC是⊙O的切线；
（2）已知⊙O的半径R=5cm，AB=8cm，求△ABD的面积.
25题图
26．(本题8分)如图，在所给的正方形网格中，每个小正方形的边长均为1个单位，每个小正方形的顶点称为格点．格点△ABD中，A(－3，5)、B(－7，2)、
D(0，2) ．
(1) 作出平行四边形ABCD，并直接写出C点坐标为_______；
(2) 作出BD的中点M；
(3) 在y轴上作出点N（不与点D重合），使得∠NAD＝∠NBD．
26题图
27．(本题10分)如图，AB为⊙O的直径，点C为⊙O上一点，若∠BAC=∠CAM，过点C作直线l垂直于射线AM，垂足为点D．
（1）试判断CD与⊙O的位置关系，并说明理由；
（2）若直线l与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°．
求图中所示阴影部分的面积．
27题图
28．(本题10分)如图，在Rt△ABC中，∠ACB＝90°，BO平分∠ABC，交AC于点O，以O为圆心，OC为半径作圆，交OB于点E．
（1）求证：AB与⊙O相切；
（2）连接CE并延长，交AB于点F，若CF⊥AB，且CF＝3，求⊙O的半径．
28题图
第24章 圆 单元检测题参考答案
1．D. 解析：A. 不能确定．因为半径不确定，故不符合题意；
B. 不能确定．因为圆心的位置不确定，故不符合题意；
C. 不能确定，因为圆心的位置不确定，故不符合题意；
D．不在同一直线上三点可以确定一个圆．故符合题意；故选D．
2．C. 解析：连接OA，∵OD⊥AB，
∴AD=AB=4，由勾股定理得，OA==5，故选C．

2题图 4题图 6题图
3．A. 解析：同圆中等弧对等弦，则命题①是真命题
垂直于弦的直径平分这条弦，则命题②是真命题
平分弦（非直径）的直径垂直于这条弦，则命题③是假命题
在同圆或等圆中，相等的圆心角所的弧相等，则命题④是假命题
综上，是真命题的有①②， 故选：A．
4．C. 解析：连接OB，∵OC＝OB，∠BCO＝20°，∴∠OBC＝20°，
∴∠BOC＝180°−20°−20°＝140°，∴∠A＝140°×＝70°，故选：C．
5．A. 解析：∵ R t △ABC中，∠ACB=90°，AC=6，AB=10，
∴，则AC=6＜BC，∴点A在⊙C内，故选：A．
6．B. 解析：连接OC，∵CP与圆O相切，∴OC⊥CP，
∵∠ACB=90°，∴AB为直径，
∵∠P=28°，∴∠COP=180°-90°-28°=62°，
而OC=OA，∴∠OCA=∠OAC，2∠CAB=∠COP，
即∠CAB=31°，故选B.
7．A. 解析：连结OB、OD，过点O作OE⊥BD于点E，
∵∠BOD＝120°，∠BOD＋∠A＝180°，
∴∠A＝60°，∠BOD＝2∠A＝120°，
∵OB＝OD，OE⊥BD，
∴∠EOD＝∠BOD＝60°，BD＝2ED，
∵OD＝2，∴OE＝1，ED＝，∴BD＝2，故选A．

7题图 9题图
8．B. 解析：∵AB是⊙O的直径，弦CD⊥AB，
∴∠OMC=90°，CM=DM．
∴∠MOC+∠MCO =90°.
∵OC∥DB，∴∠MCO=∠CDB.
又∵∠CDB=∠BOC. ∴∠MOC+∠MOC=90°.
∴∠MOC=60°.
在△OMC和△BMD中，
∴△OMC≌△BMD，∴S△OMC =S△BMD .
, 故选：B.
9．C. 解析：如图， 连接OC，
∵过点C的切线与BA的延长线交于点D，
∴∠DCO=90°, 又∵∠D=40°，
∴∠COB=90°+40°=130°，∴ 的度数是130°，
∴的度数是360°-130°=230°，
∴∠BEC=×230°=115°，故选：C；
10．D. 解析：
（1）图1，过点O作OE⊥AC，OF⊥BC，垂足为E、F，则∠OEC=∠OFC=90°
∵∠C=90°，∴四边形OECF为矩形.
∵OE=OF，∴矩形OECF为正方形.
设圆O的半径为r，则OE=OF=r，AD=AE=3-r，BD=4-r
∴3-r+4-r=5，r=1, ∴S1=π×12=π.
（2）图2，由S△ABC=×3×4=×5×CD，∴CD=
由勾股定理得：AD==，BD=5-=
由（1）得：⊙O的半径=，⊙E的半径=
∴S1+S2=π×（）2+π×（）2=π
（3）图3，由S△CDB=××=×4×MD， ∴MD=.
由勾股定理得：CM=，MB=4-=
由（1）得：⊙O的半径，
⊙E的半径=：⊙F的半径=
∴S1+S2+S3=π×（）2+π×（）2+π×（）2=π
∴图4中的S1+S2+S3+S4=π, 则S1+S2+S3+…+S10=π. 故选D．
11．C. 解：Rt△ABC中，AC＝4π，BC＝3π，∴AB＝5π，
圆在三边运动自转周数：＝3，
圆绕过三角形外角时，共自转了三角形外角和的度数：360°，即一周；
可见，⊙O自转了3+1＝4周．故选：C．
12．D. 解析：连接OE、OF、OD、OM，
∵四边形ABCD是正方形，
∴AD＝AB＝11，∠A＝90°，
∵圆O与正方形ABCD的两边AB、AD相切，
∴∠OMA＝∠OFA＝90°＝∠A，
∵OM＝OF，∴四边形AFOM是正方形，
∴AM＝OM＝5，
当点E在圆O最外端时，即：DE与圆O相切时，∠ADE最大，
∵OE＝OF，OD＝OD，∴Rt△OFD ≌Rt△OED，
∴DE＝DF＝AD –AF＝11－5＝6，故选：D．
12题图
13．70°．解析：在同圆和等圆中,同弧所对的圆心角是圆周角的2倍,所以∠COA=2∠D=70°．故答案是70°．
14．2. 解析：由题可得AD=DB=AB=4，在Rt△ADO中，
由勾股定理得OD=3，∴CD=OC-OD=5-3=2(cm), 故答案为2.
15．60°．解析：∵CD=OD=OE，∴∠C=∠DOC=20°，
∴∠EDO=∠E=40°，∴∠EOB=∠C+∠E=20°+40°=60°．故答案是：60°．
16．20° . 解析：连接OB，OA=OB，
∵OC⊥AB，∴∠BOC=∠AOC=40°，∴∠D=∠BOC=20°. 故答案为20°.

16题图 17题图
17．60. 解析：连接AD，AB，
∵MA切⊙O于A，∴AC⊥AM，
∵BD⊥AC，∴BD//AM，
∵DB=AM，∴四边形BMAD是平行四边形，
∵MA、MB分别切⊙O于A、B，
∴MA=MB，∴四边形BMAD是菱形，
∵BD⊥AC，AC过O，∴BE=DE，
∴AB=AD，∴BM=MA=AB，
∴△BMA是等边三角形，∴∠AMB=60°．故答案为：60．
18．2π．解析：∵直线AB与⊙O相切于点A，∴∠OAB＝90°．
∵AC平分∠OAB，∴∠OAC＝∠OAB＝45°．
∵OA＝OC，∴∠OAC＝∠OCA＝45°，∴∠AOC＝90°．
∴的长为： =2π．故答案是：2π．
19．34. 解析：设P (x，y)， ∴OP2=x2+y2,
∵A(-1,0)，B(1,0)，∴PA2=(x+1)2+y2, PB2=(x-1)2+y2
∴PA2+PB2=2x2+2y2+2=2(x2+y2)+2 ,
∴PA2+PB2=2OP2+2
当点P处于OC与圆的交点上时，OP取得最值,
∴OP的最小值为OC-PC=5-1=4.
∴PA2+PB2最小值为2OP2+2 =2×42+2=34.
故答案为: 34.

19题图 20题图
20．. 解析：作∠DAF与∠AB1C1的角平分线，交于点O，
过O作OF⊥AB1交AB1于点F，AB=AB1=，∠BAB1=30°，
∵四边形AB1C1D1是正方形，∠DAF与∠AB1C1的角平分线交于点O，∠BAB1=30°
∴∠OAF=30°，∠AB1O=45°.
∵OF⊥AB1， ∴B1F=OF=OA，
设B1F=x，则AF=-x， ∴（-x）2+x2=（2x）2
解得x=或x=（舍去）
即四边AB1ED的内切圆的半径为. 故答案为：.
21．解：∵BD平分∠ADC，∴∠ADB=∠CDB，
∴，∴AB=BC，∵BC=CD，∴AB=CD.
22．（1）180°；（2）相同，
(1)∵CD是直径，弦CD⊥AB，∴，
∴∠AOD=∠DOB，
∴∠AOC+∠DOB=∠AOC+∠AOD =180；
(2)相同，连接BC，
∵∠AOC=2∠ABC，∠DOB=2∠DCB，
∴∠AOC+∠DOB=2(∠CBA+∠BCD)
又∵AB⊥CD，∴∠ABC+∠DCB=90°，
∴∠AOC+∠DOB=2×90°=180°．
22题图
23．解：（1）作法如下：
①作线段AB的垂直平分线，
②作线段BC的垂直平分线，
③以两条垂直平分线的交点O为圆心，OA长为半圆画圆，
则圆O即为所求作的圆；
（2）连接OA，OC，
∵∠B＝30°，∴∠AOC＝60°，
∵OA＝OC，∴△AOC是等边三角形，
∵AC＝4，∴OA＝OC＝4，即圆的半径是4，
故答案为4．
24．（1）BC与⊙O相切，证明见解析；（2）2﹣．
解：（1）BC与⊙O相切．
证明：连接OD．
∵AD是∠BAC的平分线，
∴∠BAD＝∠CAD．
又∵OD＝OA，∴∠OAD＝∠ODA．
∴OD//AC．
∴∠ODB＝∠C＝90°，即OD⊥BC．
又∵BC过半径OD的外端点D，
∴BC与⊙O相切．

24题图
（2）设OF＝OD＝x，则OB＝OF+BF＝x+2，
根据勾股定理得：OB2＝OD2+BD2，即(x+2)2＝x2+12，
解得：x＝2，即OD＝OF＝2，
∴OB＝2+2＝4，
∵Rt△ODB中，OD＝OB，
∴∠B＝30°，∴∠DOB＝60°，
∴S扇形DOF＝＝，
则阴影部分的面积为S△ODB﹣S扇形DOF＝×2×2﹣＝2﹣．
故阴影部分的面积为2﹣．
25．（1）证明：如图，连接OA，OD.
∵点D是弧BE的中点
∴∠BOD=∠EOD=90°（四分之一圆所对的圆心角）.
∴∠ODF+∠OFD=90°.
又∵∠OFD=∠AFC, ∴∠ODF+∠AFC=90°.
又∵AC=FC, ∴∠AFC=∠CAF.
∵OA=OD, ∴∠ODF=∠OAF.
∴∠OAF+∠CAF=90°, 即∠OAC=90°.
∴AC是⊙O的切线.
（2）如图，过点B作BG⊥AD于G.
∵∠BOD=90°, OB=OD=R=5,
∴BD==5, ∠BAD=∠BOD=45°,
∵∠AGB=90°, ∴∠ABG=∠BAD=45°, ∴BG=AG.
由勾股定理得BG2+AG2=AB2，则2BG2=AB2=82,
∴BG=AG=4.
又∵DG==3,
∴AD=AG+DG=4+3=7.
.
故△ABD的面积为28cm2．
25题图
26．解：（1）分别过点B作AD的平行线、过点D作AB的平行线，两条平行线的交点即为点C，作图结果如下所示：
由平行四边形的性质可知，
点A平移到点D的平移方式与点B平移到点C的平移方式相同
∵A(-3, 5), D(0, 2)，∴点A平移到点D的平移方式为：
先向右平移3个单位长度，再向下平移3个单位长度，
∵B(-7, 2),，∴点C的坐标为C(-7+3, 2-3)，即C(-4, -1).
故答案为：C (-4, -1).
（2）平行四边形的性质：对角线互相平分
连接AC，与BD的交点即为中点M，如图所示：
（3）如图，过点A作AB的垂线，与y轴的交点即为点N，理由如下：
设BN的中点为点P，连接PA、PD
∵点P为BN的中点
∴PA为Rt△ABN斜边上的中线，PD为Rt△BDN斜边上的中线
∴PA=PB=PN，PD=PB=PN，
∴PA=PB=PD=PN.
则以点P为圆心，PA的长为半径画圆，一定经过点B，D，N，
由圆周角定理得：∠NAD=∠NBD．
26题图
27．（1）CD与⊙O相切．理由如下：
连结OC，如图，

27题图
∵OA=OC，∴∠1=∠2，
∵∠2=∠3，∴∠1=∠3，∴OC∥AD，
而CD⊥AD，∴OC⊥CD，
∴CD为⊙O的切线；
（2）解：∵∠EOC=∠1+∠2，∠2=30°，∴∠EOC=60°，
∵OC⊥CD，∴∠OCE=90°，
在Rt△OCE中，∵∠EOC=60°，OC=3，
∴OE=6,由勾股定理得，CE=33，
∴S阴影部分=S△OOE-S扇形COB
=12×3×33-60π×32360=93-3π2．
28．（1）证明：作OD⊥AB于D，如图，
∵BO平分∠ABC，OC⊥BC，OD⊥AB，
∴OD＝OC，而OC为⊙O的半径，∴AB与⊙O相切；
（2）作OH⊥CE于H，如图，设⊙O的半径为r，
∵CF⊥AB，OD⊥AB，
∴四边形OHFD为矩形，∴HF＝OD＝r，
∵OC＝OE，OH⊥CE，∴∠COH＝∠EOH，
∵OH∥BF，∴∠CBO＝∠BOH，
∵∠COH+∠BOH+∠CBO＝90°，
∴∠COH＝30°，
在Rt△OCH中，CH＝CF﹣HF＝3﹣r，
∵CH＝OC，∴3﹣r＝r，解得r＝2，
即⊙O的半径为2．
28题图