初中数学人教版九年级上册24.3 正多边形和圆教案

这是一份初中数学人教版九年级上册24.3 正多边形和圆教案，共7页。教案主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
专题24.14  正多边形和圆（专项练习）一、选择题
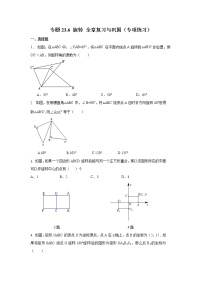
1．一个正多边形的一个内角为120°，则这个正多边形的边数为(    )A．9          B．8         C．7           D．62．如图所示，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是(    )    A． cm    B． cm    C．cm     D．1 cm                    第2题图                                第5题图3．  已知圆的半径是2，则该圆的内接正六边形的面积是（　　）　 A．3 B． 9 C． 18 D． 364．正三角形、正方形、圆三者的周长都等于，它们的面积分别为S1，S2、S3，则(    )．    A．S1＝S2＝S3    B．S3＜S1＜S2    C．S1＜S2＜S3    D．S2＜S1＜S35．中华人民共和国国旗上的五角星的画法通常是先把圆五等分，然后连接五个等分点而得到的(如图所示)．五角星的每一个角的度数是(    )．A．30°         B．35°        C．36°         D．37°              第6题图                      第7题图                第9题图6．如图所示，是由5把相同的折扇组成的“蝶恋花”（如图①）和梅花图案（如图②）（图中的折扇无重叠），则梅花图案中的五角星的五个锐角均为（   ）A．36°        B．42°          C．45°       D．48° 二、填空题7．如图所示，平面上两个正方形与正五边形都有一条公共边，则∠等于________．8．要用圆形铁片裁出边长为4的正方形铁片，则选用的圆形铁片的直径最小是________．9．如图所示，等边△ABC内接于⊙O，AB＝10cm，则⊙O的半径是________．10. 如图，点O是正五边形ABCDE的中心，则∠BAO的度数为　　．11．正六边形的半径是5cm，则边长________，周长________ ，边心距________，面积________． 12. 正六边形的外接圆的半径与内切圆的半径之比为            .三、解答题13．如图所示，正△ABC的外接圆的圆心为O，半径为2，求△ABC的边长a，周长P，边心距r，面积S． 14. 如图所示，半径为R的圆绕周长为10πR的正六边形外边作无滑动滚转，绕完正六边形后，圆一共转了多少圈？    一位同学的解答过程：圆的周长为2πR，所以它绕完正六边形后一共转了圈，结果一共转了5圈．你认为这位同学的解答有无错误？如有错误，请更正． 15．如图，已知等边△ABC内接于⊙O，BD为内接正十二边形的一边，CD=5cm，求⊙O的半径R．
【答案与解析】一、选择题1.【答案】D；【解析】可求每个外角为60°，∴  360÷60＝6或  ∴  n＝6．     2.【答案】A；【解析】较长对角线与较短对角线及一边长构成一直角三角形，用勾股定理求解．3.【答案】C；【解析】连接正六边形的中心与各个顶点，得到六个等边三角形，等边三角形的边长是2，高为3，因而等边三角形的面积是3，∴正六边形的面积=18，故选C．    4.【答案】C；【解析】当周长一定时，边数越多的正多边形其面积越大，当它成为圆时面积最大．5.【答案】C；【解析】五角星的每一个角所对的弧为圆的，∴  弧的度数为72°，因而每个角的度数为36°，故选C．6.【答案】D.【解析】如图③所示，正五边形ABCDE的中心角为72°，各内角为108°，故五角星五个锐角均为48°．  二、填空题7．【答案】72°；  【解析】＝360°－90°－90°－108°＝72°．8．【答案】；【解析】如图所示，△ABC为等腰Rt△，．9．【答案】cm；【解析】过O作OD⊥BC于D，连接OB，在Rt△BOD中，BD＝BC＝＝5(cm)．∠BOD＝，∴  ．∴  BO＝(cm)．10．【答案】54°；【解析】连接OB，则OB=OA，∴∠BAO=∠ABO，∵点O是正五边形ABCDE的中心，∴∠AOB==72°，∴∠BAO=（180°﹣72°）=54°；故答案为：54°．11．【答案】5cm，30cm，cm，；12．【答案】2：．   【解析】设正六边形的半径是r，则外接圆的半径r，
内切圆的半径是正六边形的边心距，因而是，
因而正六边形的外接圆的半径与内切圆的半径之比为2：．
 三、解答题13.【答案与解析】  作AD⊥BC于D．∵  △ABC是正三角形，∴  点O在AD上，a＝BC＝2CD，∠OCD＝30°，在Rt△COD中，，，∴  ，．又∵  AD＝OA+OD＝2+1＝3，∴  ，∴  ，，，．               14.【答案与解析】有错误，由正六边形的每个顶点外圆要转60°角，应转了（圈）．15.【答案与解析】解：连接OB，OC，OD，∵等边△ABC内接于⊙O，BD为内接正十二边形的一边，∴∠BOC=×360°=120°，∠BOD=×360°=30°，∴∠COD=∠BOC﹣∠BOD=90°，∵OC=OD，∴∠OCD=45°，∴OC=5×=5（cm）．即⊙O的半径R=5cm．