人教版九年级上册24.4 弧长及扇形的面积教学设计

专题24.16  弧长和扇形面积（专项练习）

一、选择题

1.一圆锥的侧面展开图是半径为2的半圆，则该圆锥的全面积是（     ）

A.5π           B. 4π         C.3π        D.2π

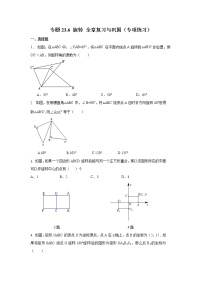
2．如图所示，边长为12m的正方形池塘的周围是草地，池塘边A、B、C、D处各有一棵树，

且AB＝BC＝CD＝3m．现用长4m的绳子将一头羊拴在其中的一棵树上，为了使羊在草地上活动区域的面积最大，应将绳子拴在(    )．

    A．A处        B．B处        C．C处       D．D处

3．劳技课上，王红制作了一顶圆锥形纸帽，已知纸帽底面圆半径为10 cm，母线长为50 cm，则制作一顶这样的纸帽所需纸的面积至少为(    )．

    A．250πcm2    B．500πcm2    C．600πcm2     D．1000πcm2

4．一圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图所对应的扇形的圆心角是(    )．

    A．120°       B．180°      C．240°       D．300°

5．底面圆半径为3cm，高为4cm的圆锥侧面积是(    )．

    A．7.5π cm2    B．12π cm2    C．15πcm2     D．24π cm2

6．  如图，半径为1的圆O与正五边形ABCDE相切于点A、C，劣弧AC的长度为（　　）

　 A．π B． π C． π D．π

二、填空题

7．已知扇形圆心角是150°，弧长为20πcm，则扇形的面积为________．

8．如图，某传送带的一个转动轮的半径为40cm，转动轮转90°传送带上的物品A被传送        厘米.

            第8题图             第9题图                  第11题图

9．如图所示，已知扇形的半径为3cm，圆心角为120°，则扇形的面积为________cm2(结果保留π)．

10. 用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是　　．

11．如图所示，把一块∠A＝30°的直角三角板ABC，在水平桌面上绕点C按顺时针方向旋转到的位置．若BC的长为15cm，求顶点A从开始到结束所经过的路径长           ．

12．如图所示，边长为1的菱形ABCD绕点A旋转，当B、C两点恰好落在扇形AEF的弧EF上时，弧BC的长度等于          ．

三、解答题

13．如图是两个半圆，点O为大半圆的圆心， AB是大半圆的弦关与小半圆相切，且AB=24．

问：能求出阴影部分的面积吗？若能，求出此面积；若不能，试说明理由．

14. 圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起，连接AC、BD．

    (1)求证：△AOC≌△BOD；

(2)若OA＝3cm，OC＝1cm，求阴影部分的面积．

15．如图所示，线段AB与⊙O相切于点C，连接OA、OB，OB交⊙0于点D，已知OA＝OB＝6cm，AB＝cm，求：(1)⊙O的半径；(2)图中阴影部分的面积．

16. 已知：如图△ABC内接于⊙O，OH⊥AC于H，过A点的切线与OC的延长线交于点D，∠B=30°，．请求出：

（1）∠AOC的度数；

（2）线段AD的长（结果保留根号）；

（3）求图中阴影部分的面积．

【答案与解析】

一、选择题
1.【答案】C .

【解析】圆锥的侧面展开图的弧长为2π，

圆锥的侧面面积为2π，底面半径为1，

圆锥的底面面积为π，则该圆锥的全面积是2π+π=3π.

故选C.

2.【答案】B 

【解析】小羊的活动区域是扇形，或是扇形的组合图形，只要算出每个扇形的面积，

即可比较出拴在B处时活动区域的面积最大．

3.【答案】B；

4.【答案】B；

【解析】由得，  ∴  ．∴  n＝180°．

5.【答案】C； 

【解析】可求圆锥母线长是5cm．

6.【答案】B；

【解析】因为正五边形ABCDE的内角和是（5﹣2）×180=540°，

则正五边形ABCDE的一个内角==108°；

连接OA、OB、OC，

∵圆O与正五边形ABCDE相切于点A、C，

∴∠OAE=∠OCD=90°，

∴∠OAB=∠OCB=108°﹣90°=18°，

∴∠AOC=144°

所以劣弧AC的长度为=π．故选B．

二、填空题

7.【答案】240πcm2 ；

【解析】先由弧长求出扇形的半径，再计算扇形的面积．

8．【答案】20π（cm）；

【解析】(cm)．

9．【答案】3π；

【解析】由扇形面积公式得(cm2)．

10．【答案】2 ；

【解析】扇形的弧长==4π，

∴圆锥的底面半径为4π÷2π=2．

故答案为：2．．

11．【答案】；

   【解析】顶点A经过的路径是一段弧，弧所在的扇形的圆心角是120°，半径AC=2BC=30cm, .

12．【答案】 ；

【解析】 连接AC，知AC＝AB＝BC，

∴  ∠BAC＝60°，

∴  弧．

三、解答题

13.【答案与解析】

将小圆向右平移，使两圆变成同心圆，如图，连OB，
过O作OC⊥AB于C点，则AC=BC=12，
∵AB是大半圆的弦且与小半圆相切，
∴OC为小圆的半径，
∴S阴影部分=S大半圆-S小半圆
=π•OB2-π•OC2
=π（OB2-OC2）
=πAC2
=72π．
故答案为72π．

14.【答案与解析】

(1)证明：同圆中的半径相等，即OA＝OB，OC＝OD．

再由∠AOB＝∠COD＝90°，得∠1＝∠2，

所以△AOC≌△BOD．

    (2)解：．

15.【答案与解析】

 (1)如图所示，连接OC，则OC⊥AB，

∴  OA＝OB，

       ∴  AC＝BC＝．

在Rt△AOC中，

．

       ∴  ⊙O的半径为3 cm．

    (2)∵  OC＝3cmOB，∠B＝30°，∠COD＝60°．

       ∴  扇形OCD的面积为．

       ∴  阴影部分的面积为 ．

16. 【答案与解析】

解：（1）∵∠B=30°，

∴∠AOC=2∠B=60°；

（2）∵∠AOC=60°，AO=CO，

∴△AOC是等边三角形；

∵OH=，

∴AO=4；

∵AD与⊙O相切，

∴AD=；

（3）∵S扇形OAC==π，S△AOD=×4×4=8；

∴．