2020-2021学年京改版七年级下册数学期末冲刺试题（word版 含答案）

这是一份2020-2021学年京改版七年级下册数学期末冲刺试题（word版 含答案），共13页。试卷主要包含了下列说法中正确的是，下列不等式变形正确的是，如图，下列条件，下列四个命题中，真命题有等内容，欢迎下载使用。

1．下列说法中正确的是（ ）
A．不循环小数是无理数B．分数不是有理数
C．有理数都是有限小数D．3.1415926是有理数
2．下列不等式变形正确的是（ ）
A．由 a＞b，得 a﹣2＜b﹣2B．由 a＞b，得|a|＞|b|
C．由 a＞b，得﹣2a＜﹣2bD．由 a＞b，得 a2＞b2
3．能够直观、形象地显示各个量在总量中所占份额的是（ ）
A．扇形统计图B．条形统计图
C．折线统计图D．频数分布直方图
4．如图，下列条件：①∠1＝∠2，②∠3+∠4＝180°，③∠5+∠6＝180°，④∠2＝∠3，⑤∠7＝∠2+∠3，⑥∠7+∠4﹣∠1＝180°中能判断直线a∥b的有（ ）
A．3个B．4个C．5个D．6个
5．下列四个命题中，真命题有（ ）
①两条直线被第三条直线所截，内错角相等．
②如果∠1和∠2是对顶角，那么∠1＝∠2．
③三角形的一个外角大于任何一个内角．
④如果x2＞0，那么x＞0．
A．1个B．2个C．3个D．4个
6．坐标平面内下列个点中，在坐标轴上的是（ ）
A．（3，3）B．（﹣3，0）C．（﹣1，2）D．（﹣2，﹣3）
7．下列方程中，不是二元一次方程的是（ ）
A．3x＝2yB．2y﹣5x＝0C．4x﹣＝0D．2x+y＝1
8．已知不等式2x﹣a≤0的正整数解恰好是1，2，3，4，5，那么a的取值范围是（ ）
A．a＞10B．10≤a≤12C．10＜a≤12D．10≤a＜12
9．如果∠A和∠B的两边分别平行，那么∠A和∠B的关系是（ ）
A．相等B．互余或互补C．互补D．相等或互补
10．下列x的值不是不等式﹣2x+4＜0的解，答案是（ ）
A．﹣2B．3C．3.5D．10
二．填空题
11．一个数的相反数是，这个数是 ．
12．把命题“锐角小于90°”改写成“如果…那么…”的形式： ．
13．已知|a+1|+＝0，则ab＝ ．
14．如图，直线AB、CD相交于点O，EO⊥AB，垂足为O，DM∥AB，若∠EOC＝35°，则∠ODM＝ 度．
15．如图，将一副三角板按如图方式叠放，则∠α等于 °．
16．在一列数a1，a2，a3，a4，…an中，已知a1＝2，a2＝，a3＝，a4＝，…an＝，则a2020＝ ．
三．解答题
17．已知关于x，y的二元一次方程组，若方程组的解互为相反数，求k的值．
18．如果不等式组的解集是0≤x＜1．求：|a+3b|﹣3（a+b）2的值．
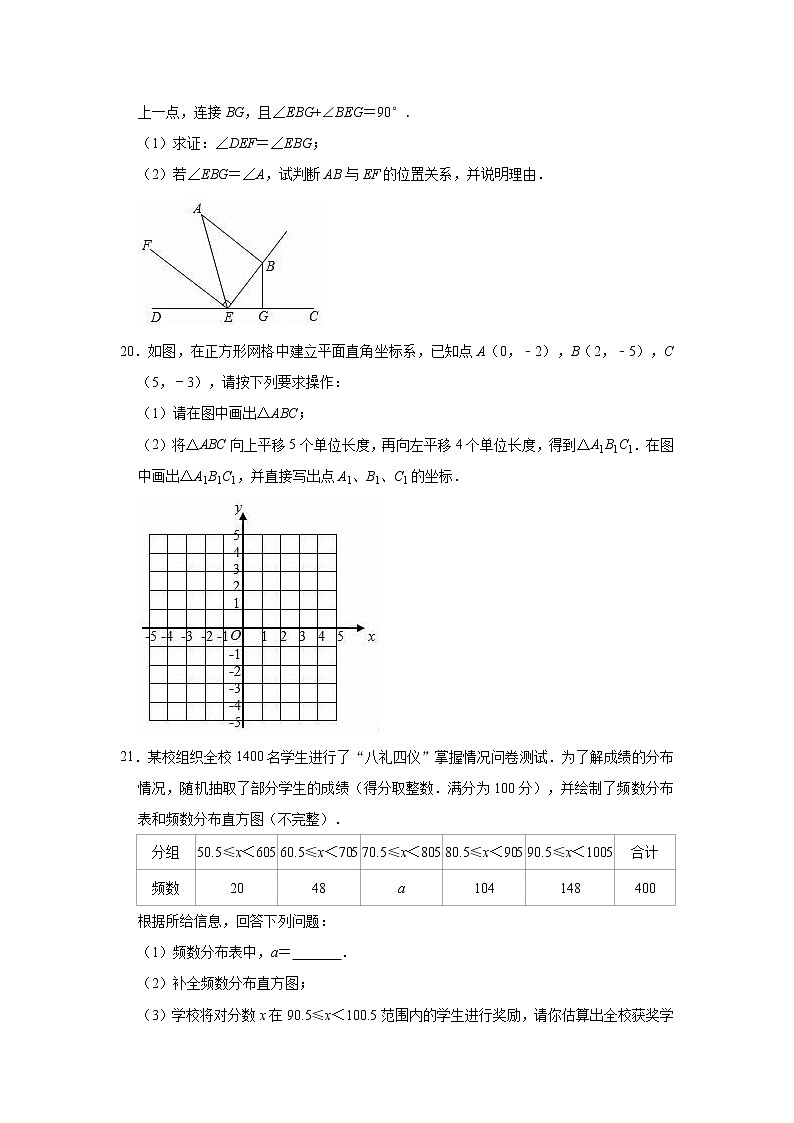
19．如图，已知点E在直线DC上，射线EF平分∠AED，过E点作EB⊥EF，G为射线EC上一点，连接BG，且∠EBG+∠BEG＝90°．
（1）求证：∠DEF＝∠EBG；
（2）若∠EBG＝∠A，试判断AB与EF的位置关系，并说明理由．
20．如图，在正方形网格中建立平面直角坐标系，已知点A（0，﹣2），B（2，﹣5），C（5，﹣3），请按下列要求操作：
（1）请在图中画出△ABC；
（2）将△ABC向上平移5个单位长度，再向左平移4个单位长度，得到△A1B1C1．在图中画出△A1B1C1，并直接写出点A1、B1、C1的坐标．
21．某校组织全校1400名学生进行了“八礼四仪”掌握情况问卷测试．为了解成绩的分布情况，随机抽取了部分学生的成绩（得分取整数．满分为100分），并绘制了频数分布表和频数分布直方图（不完整）．
根据所给信息，回答下列问题：
（1）频数分布表中，a＝ ．
（2）补全频数分布直方图；
（3）学校将对分数x在90.5≤x＜100.5范围内的学生进行奖励，请你估算出全校获奖学生的人数．
22．如图，E点为DF上的点，B为AC上的点，∠1＝∠2，∠C＝∠D．试说明：AC∥DF．
解：∵∠1＝∠2（已知），
∠1＝∠3（ ），
∴∠2＝∠3（等量代换）．
∴ ∥ （同位角相等，两直线平行）．
∴∠C＝∠ABD（ ）．
又∵∠C＝∠D（已知），
∴∠D＝∠ABD（等量代换）．
∴AC∥DF（ ）．
23．某工厂第一季度生产甲、乙两种机器共450台，改进技术后，计划第二季度生产这两种机器520台，其中甲种机器增产10%，乙种机器增产20%，该厂第二季度计划生产甲、乙机器各多少台？
24．某电视厂要印刷产品宣传材料，甲印刷厂提出：每份材料收1元印刷费，另收1000元制版费，乙厂提出：每份材料收2元印刷费，不收制版费．
（1）分别写出两厂的收费y（元）与印制数量x（份）之间的函数解析式；
（2）电视机厂拟拿出3000元用于印刷宣传材料，找哪家印刷厂印刷的宣传材料能多一些？
（3）印刷数量在什么范围时，在甲厂印刷合算？
25．在△ABC中，∠BAC＝60°，AD平分∠BAC交边BC于点D，分别过D作DE∥AC交边AB于点E，DF∥AB交边AC于点F．
（1）如图1，试判断四边形AEDF的形状，并说明理由；
（2）如图2，若AD＝4，点H，G分别在线段AE，AF上，且EH＝AG＝3，连接EG交AD于点M，连接FH交EG于点N．
（i）求EN•EG的值；
（ii）将线段DM绕点D顺时针旋转60°得到线段DM′，求证：H，F，M′三点在同一条直线上
参考答案与试题解析
一．选择题
1．解：A、无理数是无限不循环小数，故选项错误；
B、有理数包括分数，故选项错误；
C、无限循环小数也是有理数，故选项错误；
D、有限小数是有理数，故选项正确．
故选：D．
2．解：A、在不等式a＞b的两边同时减去2，不等式仍成立，即a﹣2＞b﹣2，故本选项错误；
B、当a＞b＞0时，不等式|a|＞|b|成立，故本选项错误；
C、在不等式a＞b的两边同时乘以﹣2，不等式的符号方向改变，即﹣2a＜﹣2b成立，故本选项正确；
D、当a＞b＞0时，不等式a2＞b2成立，故本选项错误；
故选：C．
3．解：条形统计图比较直观的反映各个数量的多少，
折线统计图则反映数量增减变化情况，
扇形统计图则比较直观反映各个部分占整体的百分比，
故选：A．
4．解：①由∠1＝∠2，可得a∥b；
②由∠3+∠4＝180°，可得a∥b；
③由∠5+∠6＝180°，∠3+∠6＝180°，可得∠5＝∠3，即可得到a∥b；
④由∠2＝∠3，不能得到a∥b；
⑤由∠7＝∠2+∠3，∠7＝∠1+∠3可得∠1＝∠2，即可得到a∥b；
⑥由∠7+∠4﹣∠1＝180°，∠7﹣∠1＝∠3，可得∠3+∠4＝180°，即可得到a∥b；
故选：C．
5．解：两条平行直线被第三条直线所截，内错角相等，所以①错误；
如果∠1和∠2是对顶角，那么∠1＝∠2，所以②正确；
三角形的一个外角大于任何一个不相邻的一个内角，所以③错误；
如果x2＞0，那么x≠0，所以④错误．
故选：A．
6．解：A、点（3，3）在第一象限，所以A选项错误；
B、点（﹣3，0）在x轴上，所以B选正确；
C、点（﹣1，2）在第二象限，所以C选项错误；
D、点（﹣2，﹣3）在第三象限，所以D选项错误．
故选：B．
7．解：A．3x＝2y是二元一次方程；
B．2y﹣5x＝0是二元一次方程；
C．4x﹣＝0不是整式方程，不是二元一次方程；
D．2x+y＝1是二元一次方程；
故选：C．
8．解：解不等式2x﹣a≤0得：x≤a．
根据题意得：5≤a＜6，
解得：10≤a＜12．
故选：D．
9．解：如图知∠A和∠B的关系是相等或互补．
故选：D．
10．解：不等式﹣2x+4＜0，
解得：x＞2，
则﹣2不是不等式的解．
故选：A．
二．填空题
11．解：∵一个数的相反数是，
∴这个数是：．
故答案为：．
12．解：命题“锐角小于90°”改写成“如果…那么…”的形式为：如果一个角是锐角，那么这个角小于90°；
故答案为：如果一个角是锐角，那么这个角小于90°．
13．解：由题意得，a+1＝0，b﹣2＝0，
解得a＝﹣1，b＝2，
所以，ab＝﹣1×2＝﹣2．
故答案为：﹣2．
14．解：∵EO⊥AB，
∴∠EOB＝90°，
∴∠BOC＝∠BOE+∠EOC＝90°+35°＝125°，
∵DM∥AB，
∴∠ODM＝∠BOC＝125°．
故答案为125°．
15．解：如图所示，
∵∠BAC＝∠ACD＝90°，
∴∠BAC+∠ACD＝180°，
∴AB∥CD，
∴∠1＝∠B＝45°，
∴∠α＝∠1+∠D＝75°．
故答案是75°．
16．解：∵a1＝2，
∴a2＝＝﹣1；
a3＝＝；
a4＝＝2；
…，
发现规律：每3个数一个循环，
所以2020÷3＝673…1，
则a2020＝a1＝2．
故答案为：2．
三．解答题
17．解：，
①+②得：3x+3y＝2k，即x+y＝k，
由题意得：x+y＝0，即k＝0，
解得：k＝0．
18．解：
解①得x≥4﹣2a；
解②得x＜．
∵不等式组的解集是0≤x＜1．
∴4﹣2a＝0，解得a＝2；
＝1，解得b＝﹣1．
则|a+3b|﹣3（a+b）2＝|2﹣3|﹣3×（2﹣1）2＝1﹣3＝﹣2．
19．证明：（1）∵EB⊥EF，
∴∠FEB＝90°，
又∵∠DEF+∠BEG＝180°﹣90°＝90°，∠EBG+∠BEG＝90°，
∴∠DEF＝∠EBG，
（2）AB∥EF，理由如下：
∵EF平分∠AED，
∴∠AEF＝∠DEF＝∠AED，
∵∠EBG＝∠A，∠DEF＝∠EBG，
∴∠A＝∠DEF，
又∵∠DEF＝∠AEF
∴∠A＝∠AEF，
∴AB∥EF．
20．解：（1）如图，△ABC即为所求；
（2）如图，△A1B1C1即为所求，A1（﹣4，3），B1（﹣2，0），C1（1，2）．
21．解：（1）a＝400﹣（20+48+104+148）＝80，
故答案为：80；
（2）补全频数分布直方图如下：
（3）1400×＝518（人），
答：估计全校获奖学生的人数为518人．
22．解：∵∠1＝∠2（已知），
∠1＝∠3（对顶角相等），
∴∠2＝∠3（等量代换），
∴EC∥DB（同位角相等，两直线平行），
∴∠C＝∠ABD （两直线平行，同位角相等），
又∵∠C＝∠D（已知），
∴∠D＝∠ABD（等量代换），
∴AC∥DF（内错角相等，两直线平行）．
23．解：设该厂第一季度计划生产甲机器x台，乙机器y台，由题意可知
，
解得：，
（1+10%）x＝1.1×200＝220；
（1+20%）y＝1.2×250＝300．
答：该厂第二季度生产甲机器220台，乙机器300台．
24．解：（1）甲厂的收费y（元）与印刷数量x（份）之间的函数解析式为：y＝x+1000；
乙厂的收费y（元）与印刷数量x（份）之间的函数解析式为：y＝2x；
（2）根据题意可知，若找甲厂印刷，设可以印制x份，则：3000＝x+1000，
解得：x＝2000；
若找乙厂印刷，设可以印制x份，则：3000＝2x，
解得：x＝1500．
所以，甲厂印制的宣传材料多一些；
（3）设印刷x份时，在甲厂印刷合算．
根据题意可得：x+1000＜2x，
解得：x＞1000．
∴当印制数量大于1000份时，在甲厂印刷合算．
25．（1）解：四边形AEDF的形状是菱形；理由如下：
∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∵AD平分∠BAC，
∴∠EAD＝∠FAD，
∵DE∥AC，
∴∠EDA＝∠FAD，
∴∠EAD＝∠EDA，
∴AE＝DE，
∴四边形AEDF是菱形；
（2）（i）解：连接EF交AD于点Q，如图2所示：
∵∠BAC＝60°，四边形AEDF是菱形，
∴∠EAD＝30°，AD、EF相互垂直平分，△AEF是等边三角形，
∴∠EAF＝∠AEF＝∠AFE＝60°，
∵AD＝4，
∴AQ＝2，
在Rt△AQE中，cs∠EAQ＝，即cs30°＝，
∴AE＝＝＝4，
∴AE＝AF＝EF＝4，
在△AEG和△EFH中，，
∴△AEG≌△EFH（SAS），
∴∠AEG＝∠EFH，
∴∠ENH＝∠EFH+∠GEF＝∠AEG+∠GEF＝60°，
∴∠ENH＝∠EAG，
∵∠AEG＝∠NEH，
∴△AEG∽△NEH，
∴＝，
∴EN•EG＝EH•AE＝3×4＝12；
（ii）证明：如图3，连接FM'，
∵DE∥AC，
∴∠AED＝180°﹣∠BAC＝120°，
由（1）得：△EDF是等边三角形，
∴DE＝DF，∠EDF＝∠FED＝∠EFD＝60°，
由旋转的性质得：∠MDM'＝60°，DM＝DM'，
∴∠EDM＝∠FDM'，
在△EDM和△FDM'中，，
∴△EDM≌△FDM'（SAS），
∴∠MED＝∠DFM'，
由（i）知，∠AEG＝∠EFH，
∴∠DFM'+∠EFH＝∠MED+∠AEG＝∠AED＝120°，
∴∠HFM'＝∠DFM'+∠HFE+∠EFD＝120°+60°＝180°，
∴H，F，M′三点在同一条直线上．
分组
50.5≤x＜60.5
60.5≤x＜70.5
70.5≤x＜80.5
80.5≤x＜90.5
90.5≤x＜100.5
合计
频数
20
48
a
104
148
400