数学3.5 探索与表达规律巩固练习
展开一、选择题
1.一列数按某规律排列如下:,,,,,,,,,,…,若第n个数为,则n=( )
A.50 B.60 C.62 D.71
2.如下表从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2013个格子中的整数为( )
A.3 B.2 C.0 D.﹣1
3.任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如:23=3+5,33=7+9+11,43=13+15+17+19,…按此规律,若m3分裂后其中有一个奇数是2015,则m的值是( )
A.46 B.45 C.44 D.43
4.计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳各计算结果中的个位数字的规律,猜测32017+1的个位数字是( )
A.0 B.2 C.4 D.8
5.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是103,则m的值是( )
A.9 B.12 C.11 D.10
6.下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑨个图形中菱形的个数为( )
A.73 B.81 C.91 D.109
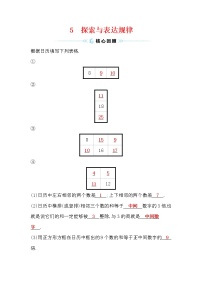
7.下列图案是用长度相同的火柴按一定规律拼搭而成,第一个图案需8根火柴,第二个图案需15根火柴,…,按此规律,第n个图案需几根火柴棒( )
A.2+7n B.8+7n C.7n+1 D.4+7n
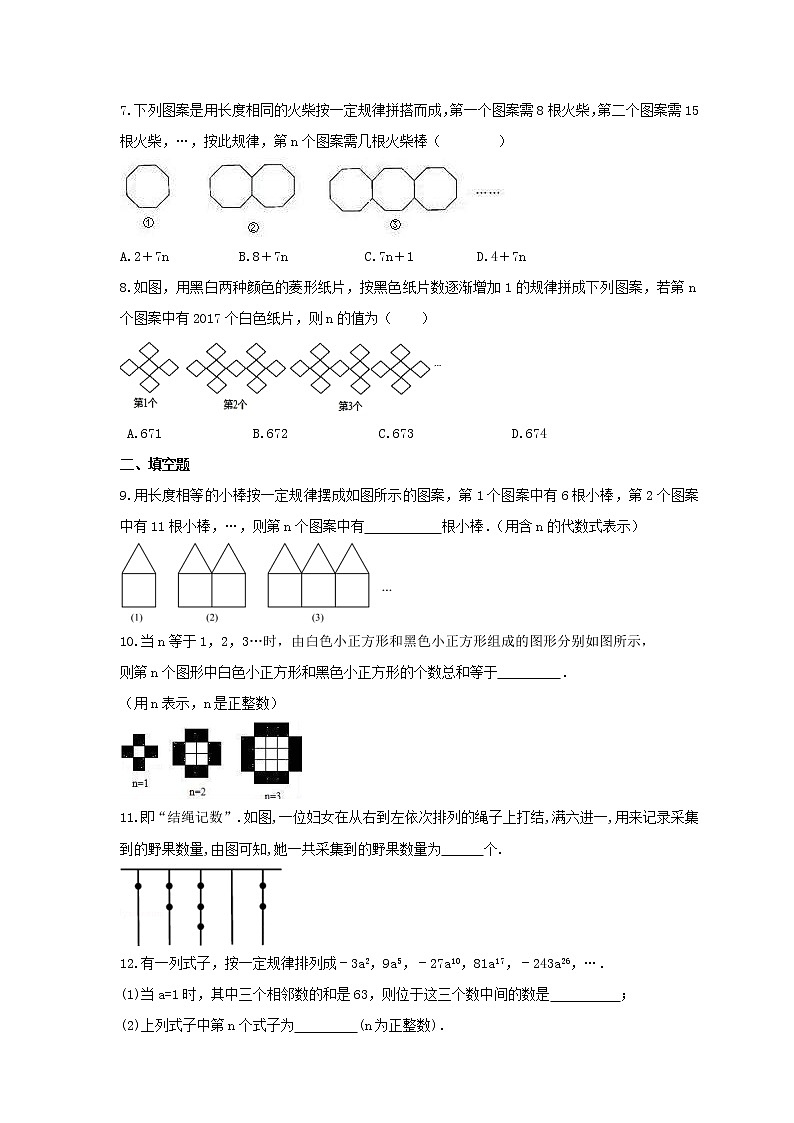
8.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2017个白色纸片,则n的值为( )
A.671 B.672 C.673 D.674
二、填空题
9.用长度相等的小棒按一定规律摆成如图所示的图案,第1个图案中有6根小棒,第2个图案中有11根小棒,…,则第n个图案中有 根小棒.(用含n的代数式表示)
10.当n等于1,2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,
则第n个图形中白色小正方形和黑色小正方形的个数总和等于 .
(用n表示,n是正整数)
11.即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为 个.
12.有一列式子,按一定规律排列成﹣3a2,9a5,﹣27a10,81a17,﹣243a26,….
(1)当a=1时,其中三个相邻数的和是63,则位于这三个数中间的数是 ;
(2)上列式子中第n个式子为 (n为正整数).
13.有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,
第2次输出的结果是6,第3次输出的结果是 ,
依次继续下去…,第2020次输出的结果是 .
14.(1)观察下列图形与等式的关系,并填空:
(2)观察下图,根据(1)中结论,计算图中黑球的个数,用含有n的代数式填空:
1+3+5+…+(2n﹣1)+( )+(2n﹣1)+…+5+3+1= .
参考答案
1.答案为:B.
解析:,,,,,,,,,,…,
可写为:,(,),(,,),(,,,),…,
∴分母为11开头到分母为1的数有11个,分别为,
∴第n个数为,则n=1+2+3+4+…+10+5=60,
2.答案为:B
3.答案为:C
4.答案为:C
5.答案为:D;
6.答案为:C.
7.答案为:C;
8.答案为:B
9.答案为:5n+1;
10.答案为:n2+4n.
11.答案为:1946.解析:2+0×6+3×6×6+2×6×6×6+1×6×6×6×6=1946.
12.答案为:(1)﹣27;(2)
13.答案为:2;
解析:根据题意得:开始输入x的值是7,可发现第1次输出的结果是7+5=12;
第2次输出的结果是×12=6;
第3次输出的结果是×6=3;
第4次输出的结果为3+5=8;
第5次输出的结果为×8=4;
第6次输出的结果为×4=2;
第7次输出的结果为×2=1;
第8次输出的结果为1+5=6;
归纳总结得到输出的结果从第2次开始以6,3,8,4,2,1循环,
∵(2020﹣1)÷6=336…5,则第2020次输出的结果为2.故答案为:2.
14.解:(1)1+3+5+7=16=42,设第n幅图中球的个数为an,
观察,发现规律:a1=1+3=22,a2=1+3+5=32,a3=1+3+5+7=42,…,
∴an﹣1=1+3+5+…+(2n﹣1)=n2.故答案为:42;n2.
(2)观察图形发现:
图中黑球可分三部分,1到n行,第n+1行,n+2行到2n+1行,
即1+3+5+…+(2n﹣1)+[2(n+1)﹣1]+(2n﹣1)+…+5+3+1,
=1+3+5+…+(2n﹣1)+(2n+1)+(2n﹣1)+…+5+3+1,
=an﹣1+(2n+1)+an﹣1=n2+2n+1+n2=2n2+2n+1.
故答案为:2n+1;2n2+2n+1.
3
a
b
c
﹣1
2
…
北师大版七年级上册3.5 探索与表达规律巩固练习: 这是一份北师大版七年级上册3.5 探索与表达规律巩固练习,共8页。试卷主要包含了单选题,填空题,应用题等内容,欢迎下载使用。
数学七年级上册3.5 探索与表达规律巩固练习: 这是一份数学七年级上册3.5 探索与表达规律巩固练习,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版七年级上册3.5 探索与表达规律课后作业题: 这是一份初中数学北师大版七年级上册3.5 探索与表达规律课后作业题,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。