中考压轴题全面突破之四：三角形的存在性(含答案13页)

这是一份中考压轴题全面突破之四：三角形的存在性(含答案13页)，共13页。
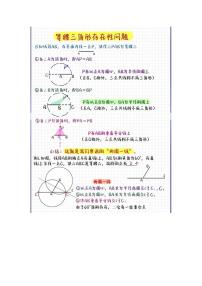
三角形的存在性问题是一类考查是否存在点，使其能构成某种特殊三角形的问题，如：直角三角形、等腰三角形、全等三角形及相似三角形的存在性．常结合动点、函数与几何，考查分类讨论、画图及建等式计算．
解题思路
①由判定定理确定三角形所满足的特殊关系；
②分类讨论，画图；
③建等式，对结果验证取舍．
对于目标三角形不确定、点的位置难以寻找等存在性问题的思考方向为：
①从角度入手，通过角的对应关系尝试画出一种情形．
②解决第一种情形．能根据几何特征表达线段长的，借助对应边成比例、或线段长转坐标代入函数表达式求解；不能直接表达线段长的，观察点的位置，考虑联立函数表达式求解．
③分类讨论，类比解决其他情形．分类时，先考虑点的位置，再考虑对应关系，用同样方法解决问题．
难点拆解
①直角三角形关键是用好直角，可考虑：勾股定理逆定理、弦图模型、直线k值乘积为1；
②等腰三角形可考虑直接表达线段长，利用两腰相等建等式，或借助三线合一找相似建等式；
③全等三角形或相似三角形关键是研究目标三角形的边角关系，进而表达线段长，借助函数或几何特征建等式．
④分类不仅要考虑图形存在性的分类，也要考虑点运动的分类．
（2012云南改编）如图，在平面直角坐标系中，抛物线 QUOTE 错误！未找到引用源。的图象经过点(2，4)，且与直线 QUOTE 错误！未找到引用源。交于A，B两点．
（1）求抛物线的函数解析式．
（2）过点A作AC⊥AB交x轴于点C，求点C的坐标．
（3）除点C外，在坐标轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．
（2009广西钦州）如图，已知抛物线 QUOTE 错误！未找到引用源。与坐标轴交于A，B，C三点，A点的坐标为(﹣1，0)，过点C的直线 QUOTE 错误！未找到引用源。与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB=5t，且0